Với giải sách bài tập Toán 6 Bài 41: Biểu đồ cột kép sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 41: Biểu đồ cột kép
a) Vẽ biểu đồ cột kép biểu diễn số cuốn truyện cửa hàng bán được các ngày trong tuần.
b) Loại truyện nào cửa hàng bán được nhiều hơn?
Lời giải:
a) Các bước vẽ biểu đồ cột kép:
Bước 1: Vẽ 2 trục ngang và dọc vuông góc với nhau
- Trục ngang ghi các ngày trong tuần.
- Trục dọc: căn cứ vào số truyện bán được nhiều nhất và ít nhất của mỗi loại.
Ta chia các khoảng cách đều là 5.
Bước 2: Tại vị trí từng đối tượng trên trục ngang, vẽ hai cột hình chữ nhật
- Cách đều nhau
- Có cùng chiều rộng
- Có chiều cao thể hiện số cuốn truyện mỗi loại bán được trong tuần, tương ứng với khoảng chia trên trục dọc.
Bước 3: Hoàn thiện biểu đồ
- Tô màu hoặc gạch chéo để phân biệt hai cột trong cột kép.
- Ghi tên biểu đồ: Số cuốn truyện cửa hàng bán được trong tuần
- Ghi tên các trục và số liệu tương ứng trên mỗi cộ:
+ Trục ngang: các ngày trong tuần (từ thứ Hai đến thứ Sáu), mỗi ngày biểu diễn hai cột (truyện tranh thiếu nhi và truyện đọc thiếu nhi).
+ Trục dọc: số cuốn truyện.
Ta có biểu đồ cột kép biểu diễn số cuốn truyện cửa hàng bán được các ngày trong tuần như sau:
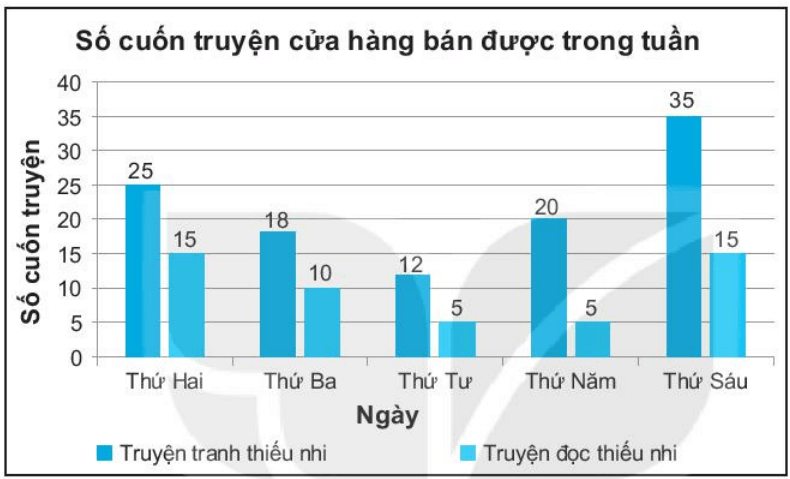
b) Cách 1: Quan sát ta thấy cột truyện tranh thiếu nhi ở tất cả các ngày đều cao hơn cột truyện đọc thiếu nhi ở tất cả các ngày.
Vậy truyện tranh thiếu nhi cửa hàng bán được nhiều hơn ở tất cả các ngày trong tuần.
Cách 2: Tính số truyện tranh và truyện đọc thiếu nhi bán được ở tất cả các ngày trong tuần rồi so sánh:
Số truyện tranh thiếu nhi bán được ở tất cả các ngày trong tuần là:
25 + 18 + 12 + 20 + 35 = 110 (cuốn truyện)
Số truyện đọc thiếu nhi bán được ở tất cả các ngày trong tuần là:
15 + 10 + 5 + 5 + 15 = 50 (cuốn truyện)
Vì 110 > 50 nên tổng số truyện tranh thiếu nhi bán được nhiều hơn số truyện đọc thiếu nhi.
Vậy truyện tranh thiếu nhi cửa hàng bán được nhiều hơn ở tất cả các ngày trong tuần.
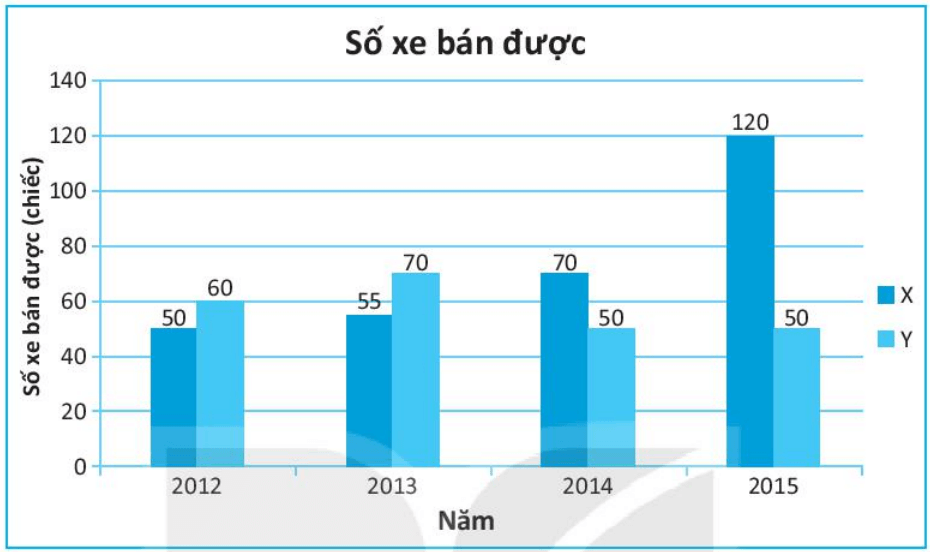
a) Năm nào mẫu xe X bán được nhiều nhất?
b) Những năm nào mẫu xe X bán được nhiều hơn mẫu xe Y?
c) Những năm nào mẫu xe Y bán được nhiều hơn mẫu xe X?
Lời giải:
a) Trong biểu đồ trên, cột bên trái biểu diễn số xe mẫu X bán được và cột bên phải biểu diễn số xe mẫu Y bán được.
Ta so sánh các cột bên trái của các năm với nhau, ta thấy cột ở năm 2015 là cao nhất nên số xe mẫu X bán được nhiều nhất vào năm 2015.
Vậy năm 2015 mẫu xe X bán được nhiều nhất với 120 chiếc.
b) Dựa vào biểu đồ, ta thấy cột biểu diễn số xe mẫu X bán được (cột bên trái) của năm 2014 và năm 2015 cao hơn cột biểu diễn số xe mẫu Y bán được (cột bên phải).
Vậy trong các năm 2014, 2015 mẫu xe X bán được nhiều hơn mẫu xe Y.
c) Dựa vào biểu đồ, ta thấy cột biểu diễn số xe mẫu Y bán được (cột bên phải) của năm 2012 và năm 2013 cao hơn cột biểu diễn số xe mẫu X bán được (cột bên trái).
Vậy trong các năm 2012, 2013 mẫu xe Y bán được nhiều hơn mẫu xe X.
Bài 9.30 trang 79 sách bài tập Toán lớp 6 Tập 2: Cho biểu đồ cột kép sau:
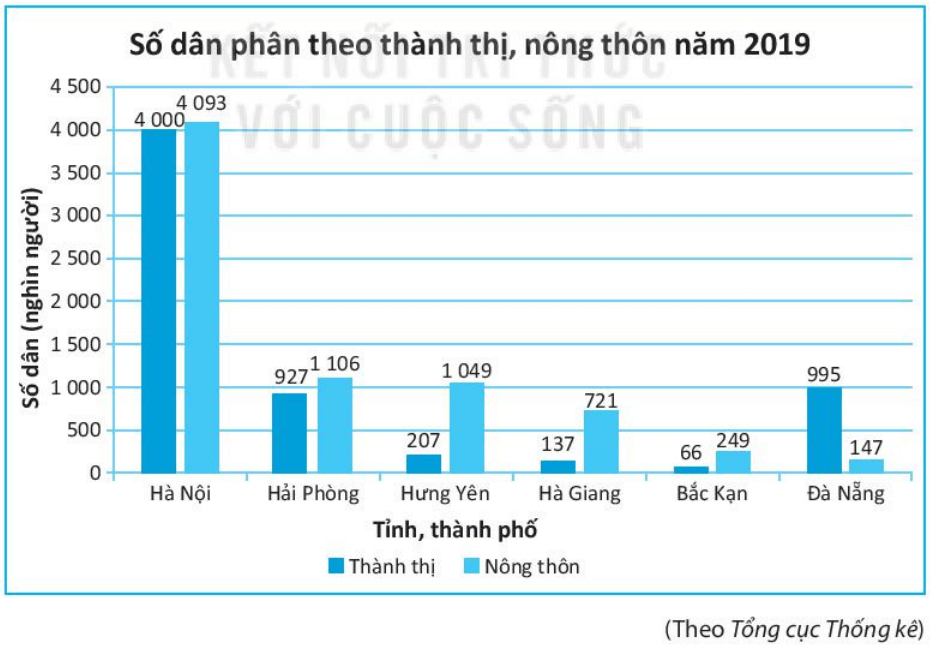
a) Năm 2019, dân số Hà Nội là bao nhiêu người? Bao nhiêu người ở thành thị, bao nhiêu người ở nông thôn?
b) Có bao nhiêu tỉnh, thành phố có số dân ở nông thôn lớn hơn số dân ở thành thị? Đó là những tỉnh, thành phố nào?
c) Lập bảng thống kê tổng số dân của các tỉnh, thành phố.
Lời giải:
a) Dân số Hà Nội năm 2019:
- Ở thành thị là 4 000 nghìn người;
- Ở nông thôn là 4 093 nghìn người.
Do đó, tổng dân số Hà Nội năm 2019 là:
4 000 + 4 093 = 8 093 (nghìn người)
Vậy năm 2019, dân số Hà Nội là 8 093 nghìn người. Trong đó, có 4 000 nghìn người ở thành thị và 4 093 nghìn người ở nông thôn.
b) Trong biểu đồ trên, ở các năm cột bên trái biểu diễn số dân ở thành thị và cột bên phải biểu thị số dân ở nông thôn.
- Ở Hà Nội: cột bên phải cao hơn cột bên trái hay số dân ở nông thôn lớn hơn số dân ở thành thị.
- Ở Hải Phòng: cột bên phải cao hơn cột bên trái hay số dân ở nông thôn lớn hơn số dân ở thành thị.
- Ở Hưng Yên: cột bên phải cao hơn cột bên trái hay số dân ở nông thôn lớn hơn số dân ở thành thị.
- Ở Hà Giang: cột bên phải cao hơn cột bên trái hay số dân ở nông thôn lớn hơn số dân ở thành thị.
- Ở Bắc Kạn: cột bên phải cao hơn cột bên trái hay số dân ở nông thôn lớn hơn số dân ở thành thị.
- Ở Đà Nẵng: cột bên phải thấp hơn cột bên trái hay số dân ở nông thôn nhỏ hơn số dân ở thành thị.
Vậy có 5 tỉnh, thành phố có số dân ở nông thôn lớn hơn số dân ở thành thị. Đó là: Hà Nội, Hải Phòng, Hưng Yên, Hà Giang, Bắc Kạn.
c) Số dân năm 2019 của các tỉnh, thành phố:
Số dân của Hà Nội là:
4 000 + 4 093 = 8 093 (nghìn người)
Số dân của Hải Phòng là:
927 + 1 106 = 2 033 (nghìn người)
Số dân của Hưng Yên là:
207 + 1 049 = 1 256 (nghìn người)
Số dân của Hà Giang là:
137 + 721 = 858 (nghìn người)
Số dân của Bắc Kạn là:
66 + 249 = 315 (nghìn người)
Số dân của Đà Nẵng là:
995 + 147 = 1 142 (nghìn người)
Ta có thống kê tổng số dân của các tỉnh, thành phố năm 2019 như sau:
|
Tỉnh, thành phố |
Hà Nội |
Hải Phòng |
Hưng Yên |
Hà Giang |
Bắc Kạn |
Đà Nẵng |
|
Số dân (nghìn người) |
8 093 |
2 033 |
1 256 |
858 |
315 |
1 142 |
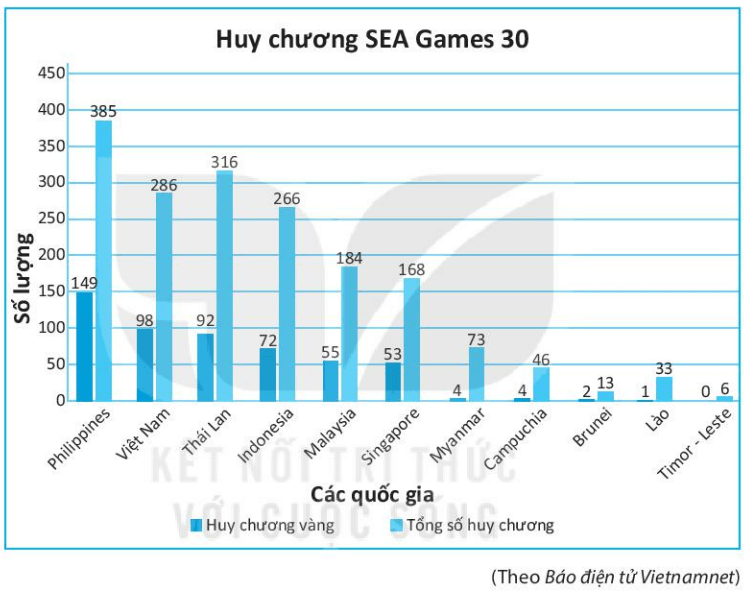
a) Kể tên ba quốc gia có số huy chương vàng nhiều nhất.
b) Sắp xếp các quốc gia theo thứ tự giảm dần về tổng số huy chương đạt được.
c) Việc xếp hạng chung cuộc căn cứ trên số huy chương vàng, nếu hai quốc gia có số huy chương vàng bằng nhau thì quốc gia nào đạt được nhiều huy chương bạc hơn sẽ được xếp trên, trường hợp số huy chương bạc vẫn bằng nhau thì việc xếp hạng sẽ dựa trên số huy chương đồng đạt được.
Theo em, Việt Nam xếp thứ mấy chung cuộc?
d) Nếu xếp hạng theo tổng số huy chương đạt được thì Việt Nam đứng thứ mấy?
Lời giải:
a) Trong biểu đồ trên, ở các quốc gia, cột bên trái biểu diễn số huy chương vàng và cột bên phải biểu diễn tổng số huy chương.
So sánh chiều cao cột bên trái của các quốc gia, chiều cao cột bên trái của ba quốc gia Philippines, Việt Nam và Thái Lan là lớn nhất.
Vậy ba quốc gia có số huy chương vàng nhiều nhất là: Philippines, Việt Nam và Thái Lan.
b) Tổng số huy chương của Philippines, Việt Nam, Thái Lan, Indonesia, Malaysia, Singapore, Myanmar, Campuchia, Brunei, Lào, Timor-Leste lần lượt là: 385; 286; 316; 266; 184; 168; 73; 46; 13; 33; 6.
Do 385 > 316 > 286 > 266 > 184 > 168 > 73 > 46 > 33 > 13 > 6.
Ta được các quốc gia theo thứ tự giảm dần về tổng số huy chương đạt được là: Philippines, Thái Lan, Việt Nam, Indonesia, Malaysia, Singapore, Myanmar, Campuchia, Lào, Brunei, Timor-Leste.
c) Số huy chương vàng của Philippines, Việt Nam, Thái Lan, Indonesia, Malaysia, Singapore, Myanmar, Campuchia, Brunei, Lào, Timor-Leste lần lượt là: 149; 98; 92; 72; 55; 53; 4; 4; 2; 1; 0.
Vì 149 > 98 > 92 > 72 > 55 > 53 > 4 > 2 > 1 > 0.
Do đó, Việt Nam là quốc gia đứng thứ hai về số huy chương vàng.
Vậy Việt Nam xếp thứ hai chung cuộc.
d) Theo câu a, tổng số huy chương đạt được của các quốc gia theo thứ tự giảm dần là: Philippines, Thái Lan, Việt Nam, Indonesia, Malaysia, Singapore, Myanmar, Campuchia, Lào, Brunei, Timor-Leste.
Vậy nếu xếp hạng theo tổng số huy chương đạt được thì Việt Nam đứng thứ ba chung cuộc.
Biểu đồ chưa hoàn thiện dưới đây biểu diễn bảng thống kê trên.
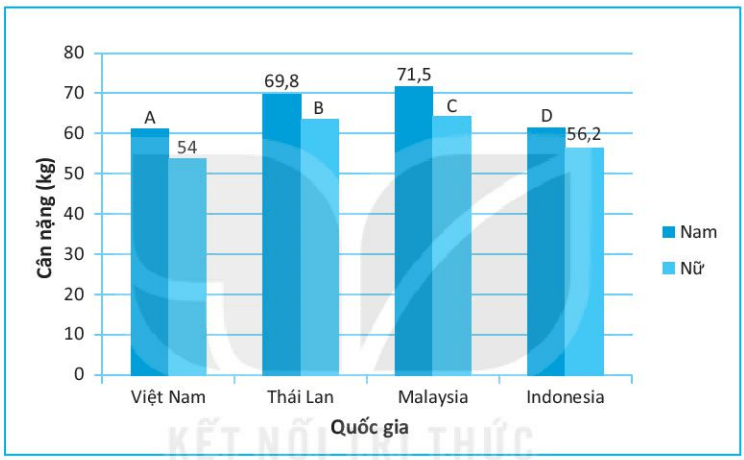
a) Các trục ngang, trục đứng của biểu đồ biểu diễn gì?
b) Hãy xác định giá trị của A, B, C, D.
Lời giải:
a) Trục ngang biểu diễn các quốc gia; trục đứng biểu diễn cân nặng (kg).
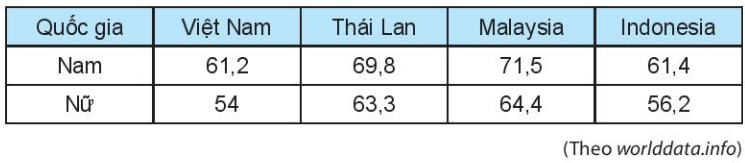
b) Đối chiếu với số liệu từ bảng thống kê:
- Giá trị A là cột bên trái của Việt Nam biểu diễn cân nặng trung bình của nam tại Việt Nam là 61,2 kg.
- Giá trị B là cột bên phải của Thái Lan biểu diễn cân nặng trung bình của nữ tại Thái Lan là 63,3 kg.
- Giá trị C là cột bên phải của Malaysia biểu diễn cân nặng trung bình của nữ tại Malaysia là 64,4 kg.
- Giá trị D là cột bên trái của Indonesia biểu diễn cân nặng trung bình của nam tại Indonesia là 61,4 kg.
Lý thuyết Biểu đồ cột kép
1. Biểu đồ cột kép
• Biểu đồ cột kép được tạo thành khi ghép hai biểu đồ cột lại với nhau.
Ví dụ:
Cho hình 1 là biểu đồ điểm của Mai
Hình 1
Cho hình 2 là biểu đồ điểm của Tiến
Hình 2
Biểu đồ cột kép thể hiện điểm của Mai và Tiến
2. Vẽ biểu đồ cột kép
• Bước 1: Vẽ hai trục ngang và dọc vuông góc với nhau:
- Trục ngang: Ghi danh sách đối tượng thống kê.
- Trục dọc: Chọn khoảng chia thích hợp với dữ liệu và ghi số ở các vạch chia.
• Bước 2: Vẽ các cột hình chữ nhật:
- Tại vị trí ghi mỗi đối tượng trên trục ngang, vẽ hai cột hình chữ nhật:
+ Sát cạnh nhau.
+ Có cùng chiều rộng.
+ Có chiều cao thể hiện hai loại số liệu của đối tượng đó, tương ứng với khoảng chia trên trục dọc.
- Các cột thể hiện cùng một bộ dữ liệu của các đối tượng thường được tô chung một màu.
• Bước 3: Hoàn thiện biểu đồ:
- Ghi tên biểu đồ
- Ghi tên các trục và ghi số liệu tương ứng trên mỗi cột (nếu có).
- Ghi chú thích cho 2 màu.
3. Phân tích số liệu với biểu đồ cột kép
• Biểu đồ cột kép được tạo thành khi ghép hai biểu đồ cột với nhau.
• Cách đọc biểu đồ cột kép:
- Nhìn theo một trục (ngang hoặc đứng) để đọc danh sách các đối tượng thống kê.
- Nhìn theo trục còn lại để đọc cặp số liệu thống kê tương ứng với các đối tượng đó.
- Lưu ý thang đo của trục số liệu khi đọc các số liệu.
- Biểu đồ cột kép dùng để so sánh từng cặp số liệu của hai bộ dữ liệu cùng loại.
- So sánh hai cột khác màu trong cùng một nhóm.
- So sánh các cột cùng màu với nhau.
Ví dụ:
Ta thấy:
- Số học sinh giỏi của các tổ của lớp 6A1 kỳ 2 đều cao hơn kỳ 1.
- Học sinh giỏi học kỳ 1 của lớp 6A1 là 3 + 2 + 6 + 1 = 12 (học sinh).
- Học sinh giỏi học kỳ 2 của lớp 6A1 là 5 + 4 + 6 + 8 = 23 (học sinh).
- Số học sinh giỏi học kỳ 2 của tổ 4 là 8 học sinh.
…
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
