Với giải sách bài tập Toán 6 Bài 7: Thứ tự thực hiện các phép tính sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 7: Thứ tự thực hiện các phép tính

Bài 1.62 trang 25 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức:

a) 3 + 4 + 5 – 7;

b) 2. 3. 4. 5: 6

Lời giải:

a) 3 + 4 + 5 – 7 = 7 + 5 – 7 = (7 – 7) + 5 = 0 + 5 = 5

b) 2. 3. 4. 5: 6 = 6. 4. 5: 6 = 4. 5. (6: 6) = 20. 1 = 20

Bài 1.63 trang 26 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức:

a) 3.10³ + 2.10² + 5.10;

b) 35 – 2.1¹¹¹ + 3.7.7²;

c) 5.4³ + 2.3 – 81.2 + 7;

Lời giải:

a) 3.10³ + 2.10² + 5.10

= 3. 1 000 + 2. 100 + 5. 10

= 3 000 + 200 + 50

= 3 200 + 50

= 3 250

b) 35 – 2.1¹¹¹ + 3.7.7²

= 35 – 2. 1 + 21. 49

= 35 – 2 + 1 029

= 33 + 1 029

= 1 062

c) 5.4³ + 2.3 – 81.2 + 7

= 5. 64 + 6 – 162 + 7

= 320 + 6 – 162 + 7

= 326 – 162 + 7

= 164 + 7

= 171

Bài 1.64 trang 26 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức:

a) [(33 – 3): 3]³⁺³;

b) 2⁵ + 2.{12 + 2.[3.(5 – 2) + 1] + 1} + 1;

Lời giải:

a) [(33 – 3): 3]³⁺³ = (30 : 3)⁶ = 10⁶ = 1 000 000

b) 2⁵ + 2.{12 + 2[3.(5 – 2) + 1] + 1} + 1

= 32 + 2 . {12 + 2 . [3 . 3 + 1] + 1} + 1

= 32 + 2 . {12 + 2 . [9 + 1] + 1} + 1

= 32 + 2 . {12 + 2 . 10 + 1} + 1

= 32 + 2 . {12 + 20 + 1} + 1

= 32 + 2 . {32 + 1} + 1

= 32 + 2 . 33 + 1

= 32 + 66 + 1

= 98 + 1

= 99.

Bài 1.65 trang 26 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức:

a) P = 2x³ + 3x² + 5x +1 khi x = 1;

b) P = a² – 2ab + b² khi a = 2; b = 1.

Lời giải:

a) Thay x = 1 vào biểu thức P ta được:

P = 2x³ + 3x² + 5x +1 = 2.1³ + 3.1² + 5.1 + 1 = 2.1 + 3.1 +5.1 + 1= 2 + 3 + 5 + 1 

    = 5 + 5 + 1 = 10 + 1 = 11

Vậy P = 11 khi x = 1.

b) Thay a = 2; b = 1 vào biểu thức P ta được:

P = a² – 2ab + b² = 2² – 2.2.1 + 1² = 4 – 4.1 + 1 = 4 – 4 + 1 = 0 + 1 = 1

Vậy P = 1 khi a = 2, b = 1.

Bài 1.66 trang 26 sách bài tập Toán lớp 6 Tập 1: Tìm số tự nhiên x thỏa mãn:

a) 16x + 40 = 10.3² + 5.(1 + 2 + 3);

b) 92 – 2x = 2.4² – 3.4 + 120 : 15;

Lời giải:

a) Ta có: 10.3² + 5.(1 + 2 + 3) = 10. 9 + 5. (3 + 3) = 90 + 5. 6 = 90 + 30 = 120 

Do đó: 16x + 40 = 120 

            16x = 120 – 40

            16x = 80

                 x = 80: 16

                 x = 5

Vậy x = 5.

b) Ta có: 2.4² – 3.4 + 120 : 15 = 2. 16 – 12 + 8 = 32 - 12 + 8 = 20 + 8 = 28

Do đó: 92 - 2x = 28 

                    2x = 92 – 28

                    2x = 64

                      x = 64: 2

                      x = 32

Vậy x = 32.

Bài 1.67 trang 26 sách bài tập Toán lớp 6 Tập 1: Lúc 6 giờ sáng. Một xe tải và một xe máy cùng xuất phát từ A đến B. Vận tốc xe tải là 50km/h; vận tốc xe máy là 30 km/h. Lúc 8 giờ sáng, một xe con cũng đi từ A đến B với vận tốc 60 km/h.

a) Giả thiết rằng có một xe máy thứ hai cũng xuất phát từ A đến B cùng một lúc với xe tải và xe máy thứ nhất nhưng đi với vận tốc 40 km/h. Hãy viết biểu thức tính quãng đường xe tải, xe máy thứ nhất và xe máy thứ hai đi được sau t giờ. Chứng tỏ rằng xe máy thứ hai luôn ở vị trí chính giữa xe tải và xe máy thứ nhất;

b) Viết biểu thức tính quãng đường xe máy thứ hai và xe con đi được sau khi xe con xuất phát x giờ;

c) Đến mấy giờ thì xe con ở chính giữa xe máy thứ nhất và xe tải?

Lời giải:

a) Sau t giờ, xe tải đi được quãng đường là: 

S₁ = 50t (km)

Sau t giờ, xe máy thứ nhất đi được quãng đường là:

S₂ = 30t (km)

Sau t giờ, xe máy thứ hai đi được quãng đường là:

S₃ = 40t (km)

Ta thấy: 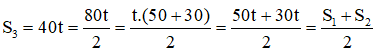 nên xe máy thứ hai luôn ở vị trí chính giữa xe tải và xe máy thứ nhất.

Vậy xe máy thứ hai luôn ở vị trí chính giữa xe tải và xe máy thứ nhất.

b) Sau x giờ, xe con đi được quãng đường là:

S = 60x (km)

Mặt khác, vì xe tải và hai xe máy cùng khởi hành sớm hơn xe con 2 giờ nên khi xe con đi được x giờ thì xe máy thứ hai đi được (x + 2) giờ, quãng đường xe máy thứ hai đi được là:

S’ = 40. (x + 2) (km)

Vậy biểu thức tính quãng đường xe con sau khi đi được x giờ là 60x km; xe máy thứ hai đi được sau khi xe con xuất phát x giờ là 40(x + 2) km.

c) Vì xe máy thứ hai luôn ở vị trí chính giữa xe tải và xe máy thứ nhất nên xe con sẽ ở chính giữa xe tải và xe máy thứ nhất khi và chỉ khi xe con đuổi kịp xe máy thứ hai, tức là:

S = S’ nên 60x = 40. (x + 2)

                    60x = 40. x + 40. 2

                     60x – 40x = 80

                       x. (60 – 40) = 80

                       x. 20 = 80

                        x = 80: 20

                        x = 4 (giờ)

Xe con sẽ ở vị trí chính giữa xe tải và xe máy thứ nhất vào lúc: 8 + 4 = 12 giờ trưa.

Vậy xe con sẽ ở vị trí chính giữa xe tải và xe máy thứ nhất vào lúc 12 giờ trưa.

Lý thuyết Thứ tự thực hiện các phép tính

+ Đối với các biểu thức không có dấu ngoặc: 

- Nếu chỉ có phép cộng và phép trừ (hoặc chỉ có phép nhân và phép chia) thì thực hiện các phép tính từ trái qua phải.

- Nếu có các phép tính cộng, trừ, nhân, chia, nâng lên lũy thừa thì ta thực hiện phép nâng lên lũy thừa trước, rồi đến nhân và chia, cuối cùng đến cộng và trừ.

Ví dụ 1. Tính giá trị biểu thức sau:

a) 23 + 47 – 52;

b) 24.5:3;

c) 2².3 + 3.7 – 18:9.

Lời giải

a) 23 + 47 – 52

= 70 – 52 

= 18.

b) 24.5:3

= 120 : 3

= 40.

c) 2².3 + 3.7 – 18:9

= 4.3 + 21 – 2

=12 + 21 – 2 

= 33 – 2 

= 31.

+ Đối với các biểu thức có dấu ngoặc: 

- Nếu chỉ có một dấu ngoặc thì ta thực hiện phép tính trong dấu ngoặc trước.

- Nếu có các dấu ngoặc tròn (), dấu ngoặc vuông [], dấu ngoặc nhọn {} thì ta thực hiện các phép tính trong dấu ngoặc tròn trước, rồi thực hiện các phép tính trong dấu ngoặc vuông, cuối cùng thực hiện các phép tính trong dấu ngoặc nhọn.

Ví dụ 2. Thực hiện phép tính

a) (30 + 80).2 + 20:4;

b) :2

Lời giải

a) (30 + 80).2 + 20:4

= 110.2 + 5

= 220 + 5

= 225.

b) :2

= :2

= :2

= :2

= 20:2

=10.