Với giải sách bài tập Toán 6 Bài 3: Thứ tự trong tập hợp các số tự nhiên sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 3: Thứ tự trong tập hợp các số tự nhiên
Lời giải:
Trên hình vẽ, điểm A biểu diễn số 7, điểm B biểu diễn số 11.
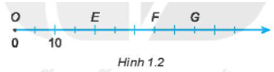
Bài 1.23 trang 12 sách bài tập Toán lớp 6 Tập 1: Mỗi điểm E, F, G trên hình 1.2 biểu diễn số nào?
Lời giải:
Ta nhận thấy điểm 10 cách O hai đoạn thẳng nên mỗi đoạn thẳng cách nhau là 5 đơn vị
+) Điểm E cách O bốn đoạn thẳng nên điểm E biểu diễn số 20
+) Điểm F cách O bảy đoạn thẳng nên điểm F biểu diễn số 35
+) Điểm G cách O chín đoạn thẳng nên điểm G biểu diễn số 45
Ghi chú: Dòng chữ “km 134” trên cột cây số cho biết nơi đó cách điểm bắt đầu của Quốc lộ 6, tức cột km0 là 134 km.
Lời giải:
Ta có 1 cây số = 1 km
+ Quan sát cột số em thấy ghi Sơn La 168 km hay vị trí đặt cột số cách Sơn La 168 km. Vậy em cần phải đi thêm 168 cây số nữa để đến Sơn La.
+ Kí hiệu O là điểm gốc (nơi có cột km0), S là điểm ứng với cột mốc tại Sơn La và H là điểm ứng với cột cây số đã cho trong hình trên. (H ứng với km134)
Ta có tia số:
(Tìm km ở vị trí S bằng cách từ 134 đếm (cộng) thêm 168, được 302).
Lời giải:
Do 54 902 < 55 699 < 55 789 < 55 806 nên sắp xếp theo các số đã cho theo thứ tự tăng dần là: 54 902; 55 699; 55 789; 55 806.
Do đó bốn điểm A, B, C và D lần lượt biểu diễn các số: 54 902; 55 699; 55 789 và 55 806.
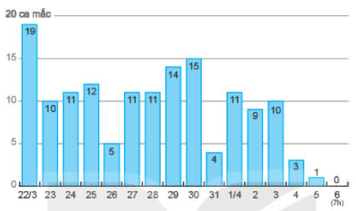
Em hãy hình dung bên trái biểu đồ là tia số biểu diễn các số 0; 5; 10; 15 và 20. Trên từng cột có ghi số ca nhiễm dịch bệnh Covid – 19 ở Việt Nam trong mỗi ngày từ ngày 22/3 đến ngày 6/4.
a) Hãy cho biết ngày nào có 5; 10; 15 ca nhiễm Covid – 19;
b) Ngày nào có nhiều ca nhiễm Covid – 19 nhất? Ngày nào ít nhất?
c) Tại sao bài báo kết luận: “Dịch bệnh Covid – 19 ở Việt Nam: Số ca nhiễm giảm dần trong những ngày gần đây”?
Lời giải:
a) Từ số liệu của biểu đồ trên, ta thấy:
+) Ngày có 5 ca nhiễm Covid – 19 là ngày 26/3
+) Ngày có 10 ca nhiễm Covid – 19 là ngày 23/3 và 3/4
+) Ngày có 15 ca nhiễm Covid – 19 là ngày 30/3
b)
+) Vì ngày 22/3 có cột biểu đồ cao nhất nên ngày 22/3 có nhiều ca nhiễm Covid – 19 nhất (19 ca)
+) Vì ngày 6/4 có cột biểu đồ thấp nhất nên ngày 6/4 có ít ca nhiễm Covid – 19 nhất
(0 ca)
c) Ta có: 10 > 3 > 1 > 0 nên trong bốn ngày liên tiếp cuối cùng, số ca nhiễm giảm dần là: 10; 3; 1; 0 nên bài báo kết luận: “Dịch bệnh Covid – 19 ở Việt Nam: Số ca nhiễm giảm dần trong những ngày gần đây”.
C = {x ∈ N* | x chẵn và x < 10} và D = {x ∈ N* | x chẵn và x ≤ 10}. Hãy mô tả các tập hợp đó bằng cách liệt kê các phần tử của chúng.
Lời giải:
+) A = {x ∈ N | x chẵn và x < 10}
Các số tự nhiên x chẵn và nhỏ hơn 10 là: 0; 2; 4; 6; 8
Vì x ∈ A do đó: A = {0; 2; 4; 6; 8}.
+) B = {x ∈ N | x chẵn và x ≤ 10}
Các số tự nhiên x chẵn và nhỏ hơn hoặc bằng 10 là: 0; 2; 4; 6; 8; 10
Vì x ∈ B do đó: B = {0; 2; 4; 6; 8; 10}.
+) C = {x ∈ N* | x chẵn và x < 10}
Các số tự nhiên x chẵn khác 0 và nhỏ hơn 10 là: 2; 4; 6; 8
Vì x ∈ C do đó: C = {2; 4; 6; 8}.
+) D = {x ∈ N* | x chẵn và x ≤ 10}
Các số tự nhiên x chẵn khác 0 và nhỏ hơn hoặc bằng 10 là: 2; 4; 6; 8; 10
Vì x ∈ D do đó: D = {2; 4; 6; 8; 10}.
Lời giải:
Các số tự nhiên x khác 0 nhỏ hơn 5 là: 1; 2; 3; 4.
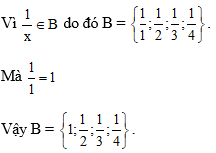
Lý thuyết Thứ tự trong tập hợp các số tự nhiên
+ Ta đã biết tập các số tự nhiên được kí hiệu là N, nghĩa là N = {0; 1; 2; 3;...}. Mỗi phần tử 0; 1; 2; 3; … được biểu diễn bởi một điểm trên tia số gốc 0 như hình vẽ:
+ Trong hai số tự nhiên khác nhau, luôn có một số nhỏ hơn số kia. Nếu số a nhỏ hơn số b thì trên tia số nằm ngang điểm a nằm bên trái điểm b. Khi đó, ta viết a < b hoặc b > a. Ta còn nói: điểm a nằm trước điểm b, hoặc điểm b nằm sau điểm a.
+ Mỗi số tự nhiên có đúng một số liền sau, chẳng hạn 9 là số liền sau của 8 (còn 8 là số liền trước của 9). Hai số 8 và 9 là hai số tự nhiên liên tiếp.
+ Nếu a < b và b < c thì a < c (tính chất bắc cầu). Chẳng hạn a < 5 và 5 < 7 suy ra a < 7.
Ví dụ 1. Viết thêm các số liền trước và số liền sau của hai số 2 567 và 3 012 để được sáu số tự nhiên và sắp xếp sáu số đó theo thứ tự giảm dần.
Lời giải
Số liền trước 2 567 là: 2 566;
Số liền sau 2 567 là: 2 568;
Số liền trước 3 012 là: 3 011;
Số liền sau 3 012 là 3 013;
Sắp xếp các số theo thứ tự giảm dần là: 3 013; 3 012; 3 011; 2 568; 2 567; 2 566.
+ Kí hiệu "≤ " và "≥"
Ta còn dùng kí hiệu a ≤ b (đọc là “a nhỏ hơn hoặc bằng b”) để nói “a < b hoặc a = b”.
Ta còn dùng kí hiệu a ≥ b (đọc là “a lớn hơn hoặc bằng b”) để nói “a > b hoặc a = b”.
Tính chất bắc cầu còn có thể viết: nếu a ≤ b và b ≤ c thì a ≤ c .
Ví dụ 2. Cho tập hợp A = {x ∈ N* | x ≤ 14}. Hãy liệt kê các phần tử của tập hợp A.
Lời giải
Các số tự nhiên khác không nhỏ hơn hoặc bằng 14 là: 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 12; 14.
A = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 12; 14} .
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
. Hãy viết tập P bằng cách liệt kê các phần tử của nó.
