Tài liệu chuyên đề Hình học phẳng và các hình học cơ bản Toán lớp 6 sách Chân trời sáng tạo gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 6.
Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 6 Chân trời sáng tạo word có lời giải chi tiết:
B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây
Xem thử tài liệu tại đây: Link tài liệu
Chuyên đề Hình học phẳng và các hình học cơ bản
Tài liệu gồm 3 chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Đoạn thẳng. Trung điểm của đoạn thẳng :
CHUYÊN ĐỀ 2. ĐOẠN THẰNG. TRUNG ĐIỂM CỦA ĐOẠN THẲNG.
PHẦN I. TÓM TẮT LÍ THUYẾT
Nhận biết đoạn thẳng, trung điểm của đoạn thẳng.
Biết số đo độ dài đoạn thẳng, vẽ đoạn thẳng trên tia.
Giải các bài toán thực tế có liên quan đến đoạn thẳng, độ dài đoạn thẳng và trung điểm của đoạn thẳng.
PHẦN II. CÁC DẠNG BÀI
Dạng 1. Nhận biết đoạn thẳng.
I. Phương pháp giải:
Mỗi đoạn thẳng có một độ dài. Độ dài đoạn thẳng là một số lớn hơn \(0\).
II. Bài toán
Bài 1:
Trên đường thẳng a lấy \(4\) điểm \(A,B,C,D\) phân biệt. Hỏi có mấy đoạn thẳng? Hãy gọi tên các đoạn thẳng ấy?
Lời giải
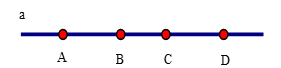
Có 6 đoạn thẳng bao gồm: \(AB,AC,AD,BC,BD,CD\)
Bài 2:
Kể tên các đoạn thẳng có trong hình dưới đây:\(\)
Lời giải
|
Các đoạn thẳng có trên hình vẽ là: \(MN,MQ,NQ,ML,LP,MP,NP\).
|
|
Bài 3:
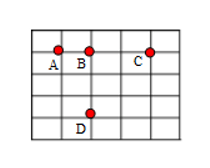
Với 4 điểm \(A,B,C,D\)như hình vẽ, em hãy kể tên các đoạn thẳng có đầu mút là:
a. Hai trong ba điểm \(A,B,C.\)
b. Hai trong 4 điểm \(A,B,C,D.\)
Lời giải
a) Các đoạn thẳng là: \(AB,AC,BC\)
b) Các đoạn thẳng là: \(AB,AC,AD,BC,BD\)
Bài 4:
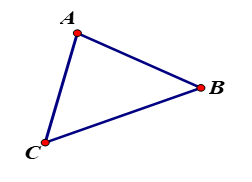
Hãy đọc tên tất cả các đoạn thẳng trong hình vẽ dưới đây:
Lời giải
Các đoạn thẳng là: \(AB,BC,AC.\)
Dạng 2. So sánh đoạn thẳng
I. Phương pháp giải: Để so sánh hai đoạn thẳng, ta thường làm như sau:
Bước 1. Đo độ dài của mỗi đoạn thẳng;
Bước 2. So sánh độ dài của các đoạn thẳng đó.
II. Bài toán
Bài 1:
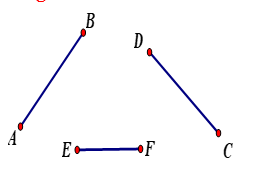
Cho các đoạn thẳng ở hình vẽ dưới đây:
a) Hãy đo độ dài các đoạn thẳng ở hình vẽ trên
b) So sánh hai độ dài của hai đoạn thẳng \({\rm{AB}}\) và \({\rm{CD}}\); \(AB\) và \({\rm{EF}}\).
Lời giải
|
a. \(AB = {\rm{ }}4{\rm{ }}cm\) \(CD = 4cm\) \(EF = 3cm\) |
b. \({\rm{AB = CD}}\) \(AB > EF\)
|
Bài 2:
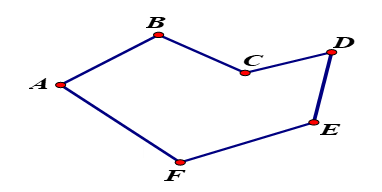
Cho hình vẽ bên: Hãy đo các đoạn thẳng \(AB,BC,DE,EF,AF\) rồi sắp xếp độ dài đoạn thẳng theo thứ tự tăng dần.
Lời giải
Đo đoạn thẳng: \(AB{\rm{ }} = {\rm{ }}3,3{\rm{ }}cm\); \(BC = 2,5cm\); \(CD = 2,6cm\); \(DE = 3,5cm\); \(EF = 3cm\); \(FA = 5,5cm\)
Sắp xếp độ dài theo thứ tự tăng dần: \(AB > CD > EF > AB > DE > FA\).
Bài 4:
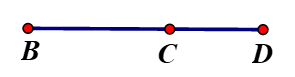
Cho ba điểm \(B,C,D\) cùng nằm trên một đường thẳng như hình vẽ. Biết \(BD = 5cm\), \(CD = 2cm\). Tính độ dài đoạn thẳng \(BC.\)
Lời giải
Theo hình vẽ, ta có: \(BD = BC + CD\)
Suy ra: \(BC = BD - CD = 5 - 2 = 3cm\).
Bài 5:
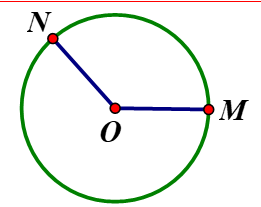
Dùng compa vẽ đường tròn tâm \(O\) có bán kính \(2\)cm. Gọi \(M\) và \(N\)là hai điểm tùy ý trên đường tròn đó. Hai đoạn thẳng \(OM\) và \(ON\) có bằng nhau không ?
Lời giải
\(OM = ON\)bằng độ dài bán kính đường tròn.
Bài 6:
a. Đo độ dài các đoạn thẳng : \(MN,NP,MP\)
b. Điền độ dài các đoạn thẳng vào chỗ chấm \(\left( {...} \right)\): \(MN + NP = ........\), \(MP = ........\)
c. So sánh \(MN + NP\)với \(MP\). Nêu nhận xét.
Lời giải
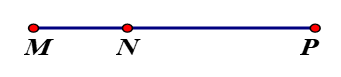
a.\(MN = 2cm\); \(NP = 4cm\); \(MP = 6cm\)
b. \(MN + NP = 2 + 4 = 6cm\); \(MP = 6cm\)
c. Nhận xét: Nếu điểm \(N\) nằm giữa hai điểm \(M\) và \(P\) thì \(MN + NP = MP\).
Dạng 3. Vẽ đoạn thẳng trên tia
I. Phương pháp giải
Cho tia \[{\rm{Ox}}\], vẽ điểm \[A\] trên tia \[{\rm{Ox}}\] sao cho \(OA = 4cm\).
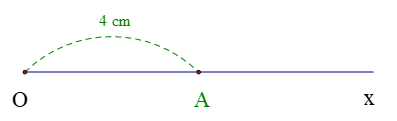
+ Trên tia \[{\rm{Ox}}\], ta luôn vẽ được một điểm \(M\) sao cho \(OM = a\left( {cm} \right)\).
Cho tia \[{\rm{Ox}}\], trên tia \[{\rm{Ox}}\] vẽ hai điểm \[A\] và \[B\] sao cho \(OA = 3cm\), \(OB = 5cm\).
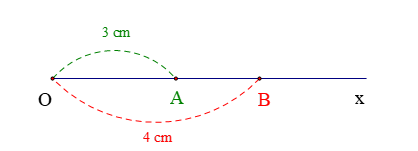
Có nhận xét gì về vị trí của điểm \[A\] so với điểm O và \[B\].
+ Trên cùng một tia \[{\rm{Ox}}\], vẽ hai điểm \[A\] và \[B\], nếu \(OA < OB\) thì điểm \[A\] nằm giữa hai điểm \[O\]và \[B\].
+ Trên cùng một tia \[{\rm{Ox}}\], vẽ ba điểm \[A,B,C\] nếu \(OA < OB < OC\) thì \[B\] nằm giữa \[A\] và \[C\].
II. Bài toán.
Bài 1:
Trên tia \({\rm{Ox}}\), vẽ hai điểm \(M\) và \(N\) sao cho \(OM = 2cm\), \(ON = 4cm\).
a. Trong ba điểm \(O,M,N\) điểm nào nằm giữa hai điểm còn lại.
b. Tính độ dài đoạn \(MN\).
Lời giải
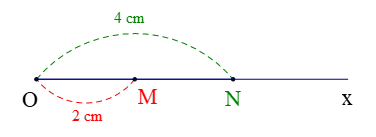
a. Trên tia \({\rm{Ox}}\), vẽ hai điểm \(M\) và \(N\) sao cho \(OM = 2cm\), \(ON = 4cm\) (\(OM < ON)\) nên điểm \(M\) nằm giữa hai điểm \(O\) và \(N\).
b. Vì điểm \(M\) nằm giữa hai điểm \(O\) và \(N\) nên \(OM + MN = ON\)
hay \(MN = ON - OM = 4 - 2 = 2cm\)
Bài 2:
Trên tia \({\rm{Ox}}\), vẽ ba điểm \(A,B,C\) sao cho \(OA = 3cm\), \(OB = 5cm\) và \(OC = 6cm\).
a. Trong ba điểm \(O,B,C\) điểm nào nằm giữa ba điểm còn lại.
b. Trong ba điểm \(A,B,C\) điểm nào nằm giữa hai điểm còn lại.
c. Tính độ dài đoạn \(AB\) và độ dài đoạn \(BC\).
Lời giải
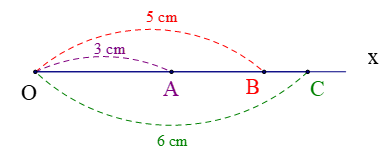
a. Trên tia \({\rm{Ox}}\), vẽ ba điểm \(B,C\) sao cho \(OB = 5cm\) và \(OC = 6cm\) ta có: \(OB < OC\) nên điểm \(B\) nằm giữa hai điểm \(O\) và \(C\).
b. Trên tia \({\rm{Ox}}\), vẽ ba điểm \(A,B,C\) sao cho \(OA = 3cm,OB = 5cm\) và \(OC = 6cm\) ta có: \(OA < OB < OC\) nên điểm \(B\) nằm giữa hai điểm \(A\) và \(C\).
c. Vì điểm \(B\) nằm giữa hai điểm \(O\) và \(C\)nên \(OB + BC = OC\)
hay \(BC = OC - OB = 6 - 5 = 1(cm)\)
Trên tia \({\rm{Ox}}\) có \(OA = 3cm\), \(OB = 5cm\) \((OA < OB)\) nên điểm \(A\) nằm giữa hai điểm \(O\) và \(B\).
Do đó: \(OA + AB = OB\)
Hay \(AB = OB - OA = 5 - 3 = 2(cm)\)
Bài 3:
Trên tia \({\rm{Ax}}\) lấy hai điểm \(B\) và \(C\) sao cho \(AB = 3cm\), \(AC = 4cm\).
a. Tính độ dài đoạn \(BC\).
b. Vẽ tia \({\rm{Ay}}\) là tia đối của tia \({\rm{Ax}}\), trên tia \({\rm{Ay}}\) lấy điểm \(D\) sao cho \(AD = 3cm\). Tính \(BD\) và \(CD\).
Lời giải
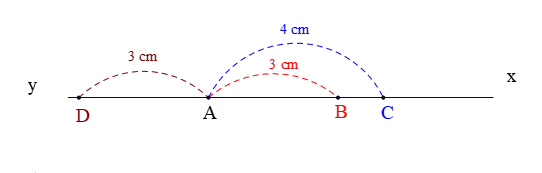
a. Trên tia \({\rm{Ax}}\): \(AB = 3cm\), \(AC = 4cm\). Vì \(AB < AC\) nên điểm \(B\) nằm giữa hai điểm \(A\) và \(C\).
Do đó: \(AB + BC = AC\)
Hay \(BC = AC - AB = 4 - 3 = 1(cm)\).
b. Vì tia \({\rm{Ay}}\) là tia đối của tia \({\rm{Ax}}\), trên tia \({\rm{Ay}}\) lấy điểm \(D\), trên tia \({\rm{Ax}}\) lấy hai điểm \(B\) và \(C\) nên điểm \(A\) nằm giữa hai điểm \(D\) và \(C\); điểm \(A\) nằm giữa hai điểm \(D\) và \(B\).
+ Ta có: \(DA + AB = DB\)
Hay \(BD = 3 + 3 = 6(cm)\)
+ Có: \(DA + AC = CD\)
Hay \(CD = 3 + 4 = 7(cm)\)
Vậy \(BD = 6cm;CD = 7cm\).
Bài 4:
Cho đoạn thẳng \(AB = 5cm\). Trên đoạn \(AB\) lấy điểm \(C\) sao cho \(AC = 3cm\).
a. Tính \(BC\).
b. Lấy điểm \(D\) thuộc tia đối của tia \(BC\) sao cho \(BD = 2cm\). So sánh độ dài \(CD\) và \(AB\).
Lời giải
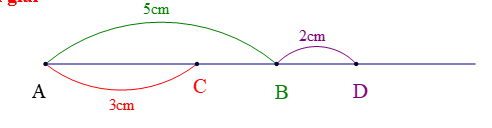
a. Vì điểm \(C\) thuộc đoạn \(AB\) nên \(AC + CB = AB\)
hay \(CB = AB - AC = 5 - 3 = 2(cm)\)
b. Ta có điểm \(D\) thuộc tia đối của tia \(BC\), điểm \(C\) thuộc đoạn \(AB\) nên điểm \(B\) nằm giữa hai điểm \(D\) và \(C\).
Do đó: \(CB + BD = CD\)
hay \(CD = 2 + 2 = 4(cm)\)
Vậy \(CD < AB(4cm < 5cm)\)
Bài 5:
Cho đường thẳng \(xy\). Điểm \(O\) thuộc đường thẳng \(xy\). Trên tia \(Oy\) lấy hai điểm \(A\) và \(B\) sao cho \(OA = 3cm\), \(OB = 5cm\).
a. Tính đoạn thẳng \(AB\).
b. Lấy \(C\) điểm thuộc tia \[{\rm{Ox}}\] sao cho \(AC = 6cm\). Chứng minh \(OA = OC\).
Lời giải
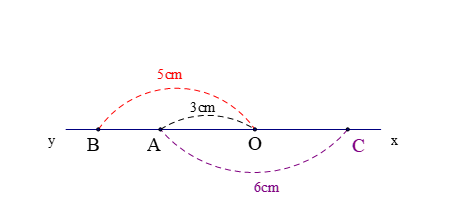
a. Trên tia \(Oy\) lấy hai điểm \(A\) và \(B\): \(OA = 3cm\), \(OB = 5cm\) có \(OA < OB\) nên điểm \[A\] nằm giữa hai điểm \[O\]và \[B\].
Do đó: \(OA + AB = OB\)
Hay \(AB = OB - OA = 5 - 3 = 2(cm)\)
b. Vì điểm \(O\) thuộc đường thẳng \(xy\), mà điểm \(A\) thuộc tia \(Oy\) nên điểm \[O\] nằm giữa hai điểm \[A\] và \[C\]
Do đó: \(AO + OC = AC\)
hay \(OC = AC - OA = 6 - 3 = 3(cm)\)
Vậy \(OA = OC = 3cm\).