Với tóm tắt lý thuyết Toán lớp 8 Bài 25: Phương trình bậc nhất một ẩn sách Kết nối tri thức hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 8.

Lý thuyết Toán lớp 8 Bài 25: Phương trình bậc nhất một ẩn

A. Lý thuyết Phương trình bậc nhất một ẩn

1. Phương trình một ẩn

Khái niệm:

Một phương trình với ẩn x có dạng $A\left(x\right)=B\left(x\right)$, trong đó vế trái A(x) và vế phải B(x) là hai biểu thức có cùng một biến x.

Ví dụ: $3x--1=2x+3;3x=5$ là các phương trình ẩn x.

Số $x_0$ là nghiệm của phương trình $A\left(x\right)=B\left(x\right)$nếu giá trị của A(x) và B(x) tại $x_0$ bằng nhau.

Ví dụ: $x=2$ là nghiệm của phương trình $2x=x+2$ vì thay $x=2$ vào phương trình, ta được 2.2 = 2 + 2

Giải một phương trình là tìm tất cả các nghiệm của nó.

Chú ý: Tập hợp tất cả các nghiệm của một phương trình được gọi là tập nghiệm của phương trình đó và kí hiệu là S.

Ví dụ: Giải phương trình: $3x+6=0$

Ta có: $3x+6=0\iff 3x=-6\iff x=-2$

Vậy tập nghiệm của phương trình là S = {-2}

2. Phương trình bậc nhất một ẩn và cách giải

Khái niệm: Phương trình dạng ax + b = 0, với a, b là hai số đã cho và $a\ne 0$, được gọi là phương trình bậc nhất một ẩn x.

Cách giải:

Phương trình bậc nhất ax + b = 0 ($a\ne 0$) được giải như sau:

$\begin{array}{c}ax+b=0\\ ax=-b\\ x=-\frac{b}{a}\end{array}$

Phương trình bậc nhất ax + b = 0 ($a\ne 0$) luôn có một nghiệm duy nhất là $x=-\frac{b}{a}$.

Ví dụ: Giải phương trình: $3x+11=0$

Ta có: $3x+11=0\iff 3x=-11\iff x=-\frac{11}{3}$

Vậy nghiệm của phương trình là $x=-\frac{11}{3}$.

3. Phương trình đưa được về dạng ax + b = 0

Bằng cách chuyển vế và nhân cả hai vế của phương trình với một số khác 0, ta có thể đưa một số phương trình ẩn x về phương trình dạng ax + b = 0 và do đó có thể giải được chúng.

Ví dụ: Giải phương trình: $7x--\left(2x+3\right)=5\left(x--2\right)$

$\begin{array}{c}11x--\left(2x+3\right)=6\left(x--2\right)\\ 11x-2x-3=6x-12\\ 11x-2x-6x=-12+3\\ 3x=-9\\ x=\frac{-9}{3}\\ x=-3\end{array}$

Vậy nghiệm của phương trình là x = -3

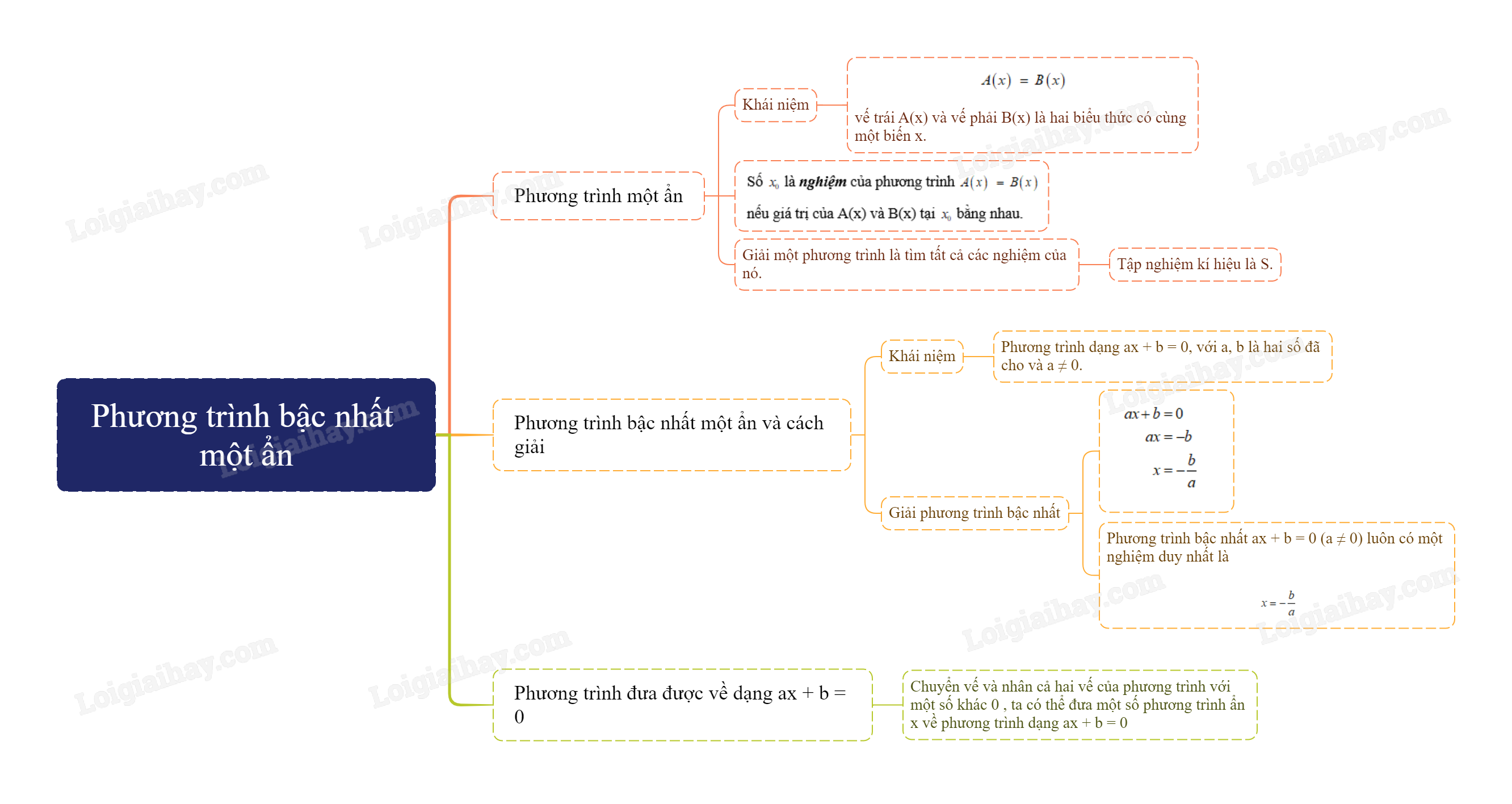
Sơ đồ tu duy Phương trình bậc nhất một ẩn

B. Bài tập Phương trình bậc nhất một ẩn

Đang cập nhật...

Xem thêm các bài tóm tắt lý thuyết Toán lớp 8 Kết nối tri thức hay, chi tiết khác:

Lý thuyết Bài 24: Phép nhân và phép chia phân thức đại số

Lý thuyết Bài 25: Phương trình bậc nhất một ẩn

Lý thuyết Bài 26: Giải bài toán bằng cách lập phương trình

Lý thuyết Bài 27: Khái niệm hàm số và đồ thị của hàm số

Lý thuyết Bài 28: Hàm số bậc nhất và đồ thị của hàm số bậc nhất

Lý thuyết Bài 29: Hệ số góc của đường thẳng