Với tóm tắt lý thuyết Toán lớp 6 Bài 10: Số nguyên tố. Hợp số sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 6.
Lý thuyết Toán lớp 6 Bài 10: Số nguyên tố. Hợp số
Video giải Toán 6 Bài 10: Số nguyên tố. Hợp số - Cánh diều
A. Lý thuyết Số nguyên tố. Hợp số
• Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.
• Hợp số là số tự nhiên lớn hơn 1, có nhiều hơn hai ước.
Lưu ý:
+ Số 0 và số 1 không là số nguyên tố và cũng không là hợp số.
+ Để chứng tỏ số tự nhiên a lớn hơn 1 là hợp số, ta chỉ cần tìm một ước của a khác 1 và khác a.
Ví dụ:
+ Số 7 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 7.
+ Số 10 là hợp số vì ngoài hai ước là 1 và 10, nó còn ít nhất 1 ước nữa là 2.
Lưu ý: Nếu số nguyên tố p là ước của số tự nhiên a thì p được gọi là ước nguyên tố của a.
Ví dụ:
+ Số 39 có các ước là 1, 3, 13, 39, trong đó 3 và 13 là số nguyên tố. Vậy các ước nguyên tố của 39 là 3 và 13.
+ Số 17 là số nguyên tố. Vậy ước nguyên tố của 17 là 17.
Nhận xét: Số nguyên tố nhỏ nhất là số 2 và đó là số nguyên tố chẵn duy nhất.
B. Bài tập tự luyện
Bài 1. Cho các số 36, 37, 69, 75. Trong các số đó:
a) Số nào là số nguyên tố? Vì sao?
b) Số nào là hợp số? Vì sao?
Lời giải:
a) Số 37 là số nguyên tố vì nó lớn hơn 1, chỉ có hai ước là 1 và 37.
b) Ta có
+ Số 36 có chữ số tận cùng là 6 nên nó chia hết cho 2.
Do đó số 36 là hợp số vì ngoài hai ước là 1 và 36, nó còn có ít nhất một ước nữa là 2.
+ Số 69 có tổng các chữ số là 6 + 9 = 15 chia hết cho 3 nên số 69 chia hết cho 3.
Do đó số 69 là hợp số vì ngoài hai ước là 1 và 69 thì nó còn có ít nhất một ước nữa là 3.
+ Số 75 có chữ số tận cùng là 5 nên nó chia hết cho 5.
Do đó 75 là hợp số vì ngoài hai ước là 1 và 75, nó còn có ít nhất một ước nữa là 5.
Bài 2. Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1 với n là số tự nhiên bất kì.
Lời giải:
Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số.
Thật vậy,
+ Với số dư là 0 thì a chia hết cho 4 nên a là hợp số
+ Với số dư là 2, ta có: a = 4n + 2
Vì 4 chia hết cho 2 nên 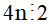 , 2 chia hết cho 2
, 2 chia hết cho 2
Do đó: 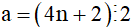 nên a là hợp số
nên a là hợp số
Ta xét trường hợp số dư là 1 và 3.
+ Với mọi trường hợp số dư là 1 ta có a = 4n + 1
+ Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 – 1 = 4(n + 1) – 1
Đặt n + 1 = m, khi đó a = 4m – 1
Từ đó suy ra điều phải chứng minh.
Xem thêm các bài tóm tắt lý thuyết Toán 6 Cánh diều hay, chi tiết khác:
Lý thuyết Bài 9: Dấu hiệu chia hết cho 3, cho 9
Lý thuyết Bài 10: Số nguyên tố. Hợp số
Lý thuyết Bài 11: Phân tích một số ra thừa số nguyên tố
Lý thuyết Bài 12: Ước chung và ước chung lớn nhất
Lý thuyết Bài 13: Bội chung và bội chung nhỏ nhất