Với tóm tắt lý thuyết Toán lớp 4 Phân số bằng nhau. Rút gọn phân số hay, chi tiết cùng với 25 bài tập chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 4.

Lý thuyết Phân số bằng nhau. Rút gọn phân số lớp 4 hay, chi tiết

A. Lý thuyết Phân số bằng nhau. Rút gọn phân số

I. KIẾN THỨC CƠ BẢN

Lý thuyết:  

Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

Khi rút gọn phân số có thể làm như sau: 

Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Ví dụ: Rút gọn phân số  .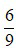

Ta thấy 6 và 9 đều chia hết cho 3 nên: 

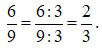
2 và 3 không cùng chia shết cho một số tự nhiên nào lớn hơn 1 nên phân số 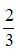 không thể rút gọn được nữa. Ta nói rằng phân số 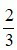là phân số tối giản và phân số  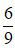đã được rút gọn thành phân số tối giản .

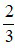II. CÁC DẠNG TOÁN

Dạng 1: Tìm phân số bằng nhau

Phương pháp: 

Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Nếu cả tử số và mẫu số của một phân số cùng chia hết cho một số tự nhiên khác 0 thì sau khi chia ta được một phân số bằng phân số đã cho.

Ví dụ: Phân số nào dưới đây bằng với phân số  ?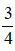

Lời giải: 

Ta có:

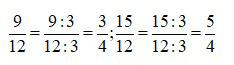
Vậy trong các phân số đã cho, phân số bằng phân số là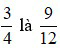  

Dạng 2: Rút gọn phân số

Phương pháp: 

Khi rút gọn phân số có thể làm như sau: 

Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản.

Ví dụ: Rút gọn các phân số: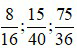  

Lời giải:

Ta thấy cả 8 và 16 đều chia hết cho 8 nên:  .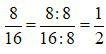

Ta thấy cả 15 và 40 đều chia hết cho 5 nên:  .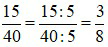

Ta thấy cả 75 và 36 đều chia hết cho 3 nên:  .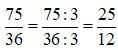

Dạng 3: Tìm phân số tối giản

Phương pháp: 

Phân số tối giản có tử số và mẫu số không cùng chia hết cho một số tự nhiên nào lớn hơn 1.

Ví dụ: Trong các phân số sau đây:  .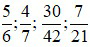

Phân số nào là phân số tối giản, phân số nào không là phân số tối giản? Nếu phân số đã cho không là phân số tối giản thì hãy rút gọn phân số đó.

Lời giải:

Phân số 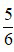 : Ta thấy 5 và 6 không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên phân số  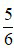 là phân số tối giản.

Phân số 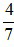 : Ta thấy 4 và 7 không cùng chia hết cho một số tự nhiên nào lớn hơn 1 nên phân số  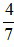 là phân số tối giản.

Phân số 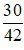 : Ta thấy 30 và 42 đều chia hết cho 6 nên:  .

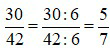Phân số 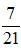 : Ta thấy 7 và 21 đều chia hết cho 7 nên:  .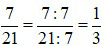