Tailieumoi.vn xin giới thiệu bộ đề thi giữa kì 1 môn Toán lớp 11 sách Kết nối tri thức năm 2024 - 2025. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi Giữa học kì 1 Toán 11. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi giữa học kì 1 Toán 11 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận tài liệu.

Xem thử tài liệu tại đây: Link tài liệu

Đề thi giữa kì 1 Toán 11 Kết nối tri thức có đáp án năm 2024

Đề thi giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2024 - 2025

Môn: Toán lớp 11

Thời gian làm bài: phút

(Đề số 1)

I. Trắc nghiệm (7 điểm)

Câu 1. Đổi số đo của góc $\alpha =30°$ sang rađian.

A. $\alpha =\frac{\pi }{2}.$

B. $\alpha =\frac{\pi }{4}.$

C. $\alpha =\frac{\pi }{6}.$

D. $\alpha =\frac{\pi }{3}.$

Câu 2. Cho $0<\alpha <\frac{\pi }{2}.$ Khẳng định nào sau đây đúng?

A. $\cot \left(\alpha +\frac{\pi }{2}\right)>0.$

B. $\cot \left(\alpha +\frac{\pi }{2}\right)\ge 0.$

C. $\tan \left(\alpha +\pi \right)<0.$

D. $\tan \left(\alpha +\pi \right)>0.$

Câu 3.Công thức nào dưới đây SAI?

A. $\tan \left(a-b\right)=\frac{\tan a-\tan b}{1+\tan a\tan b}$.

B. $\cos a\cos b=\frac{1}{2}\left(\text{cos}\left(a-b\right)+\text{cos}\left(a+b\right)\right)$.

C. $\sin a\cos b=\frac{1}{2}\left(\text{sin}\left(a-b\right)+\text{sin}\left(a+b\right)\right)$.

D. $\sin a\sin b=\frac{1}{2}\left(\text{cos}\left(a-b\right)+\text{cos}\left(a+b\right)\right)$.

Câu 4. Rút gọn $M=\sin \left(x+y\right)\cos y-\cos \left(x+y\right)\sin y$?

A. $M=\cos x$.

B. $M=\sin x$.

C. $M=\sin \left(x+2y\right)$.

D. $M=\cos \left(x+2y\right)$.

Câu 5. Cho hàm số $y=f\left(x\right)$có đồ thị như hình vẽ.

Đồ thị hàm số là đồ thị của hàm số nào dưới đây?

A. $y=\tan x$.

B. $y=\sin x$.

C. $y=\cos x$.

D. $y=\cot x$.

Câu 6. Trong các khẳng định sau, khẳng định nào sai ?

A.Tập xác định của hàm số $y=\cot x$là $ℝ\backslash \left(\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)$.

B. Tập xác định của hàm số $y=\sin x$là $ℝ$.

C. Tập xác định của hàm số $y=\cos x$là $ℝ$.

D. Tập xác định của hàm số $y=\tan x$là $ℝ\backslash \left(\frac{\pi }{2}+k\pi ,k\in \mathbb{Z}\right)$

Câu 7. Trong các hàm số cho dưới đây, hàm số nào là hàm số tuần hoàn?

A. $y=\tan x$.

B. $y=x^2+\tan x$.

C. $y=x^2$.

D. $y=x^2\tan x$.

Câu 8. Phương trình $\tan x=\sqrt{3}$ có tập nghiệm là

A. $\left(\frac{\pi }{3}+k2\pi ,k\in \mathbb{Z}\right)$.

B. $\varnothing$.

C. $\left(\frac{\pi }{3}+k\pi ,k\in \mathbb{Z}\right)$.

D. $\left(\frac{\pi }{6}+k\pi ,k\in \mathbb{Z}\right)$.

Câu 9. Nghiệm của phương trình $\cos x=-\frac{1}{2}$ là

A. $x=\pm \frac{2\pi }{3}+k2\pi$.

B. $x=\pm \frac{\pi }{6}+k\pi$ .

C. $x=\pm \frac{\pi }{3}+k2\pi$.

D. $x=\pm \frac{\pi }{6}+k2\pi$.

Câu 10. Phương trình nào dưới đây tương đương với phương trình $x+1=0$?

A. $x^2-1=0$ .

B. $\frac{x+1}{x-1}=0$ .

C. $x^2-2x+1=0$ .

D. $\frac{x^2+2x+1}{x+1}=0$ .

Câu 11. Cho dãy số $\left(u_n\right)$ là dãy số tự nhiên lẻ theo thứ tự tăng dần và $u_1=3$. Năm số hạng đầu của dãy số $\left(u_n\right)$ là:

A. $1;3;5;7;9$.

B. $1,2,3,4,5$.

C. $3,5,7,9,11$.

D. $0,1,3,5,7$.

Câu 12. Cho dãy số $\left(u_n\right)$ được xác định bởi $\left(\begin{array}{c}{u}_1=3\\ u_{n+1}=u_n-2\end{array}\right),\forall n\in {\mathbb{N}}^{*}$. Khẳng định nào sau đây đúng?

A. $\left(u_n\right)$ là dãy số tăng.

B. $\left(u_n\right)$ là dãy số giảm.

C. $\left(u_n\right)$ không là dãy số tăng cũng không là dãy số giảm .

D. $\left(u_n\right)$ là dãy số không đổi.

Câu 13. Trong các dãy số sau, dãy số nào là một cấp số cộng?

A. $1;-3;-7;-11;-15;\cdots$

B. $1;-3;-6;-9;-12;\cdots$

C. $1;-2;-4;-6;-8;\cdots$

D. $1;-3;-5;-7;-9;\cdots$

Câu 14. Cho dãy số $\frac{1}{2};0;-\frac{1}{2};-1;-\frac{3}{2};\mathrm{.....}$ là cấp số cộng với:

A. Số hạng đầu tiên là $\frac{1}{2}$, công sai là $\frac{1}{2}$

B. Số hạng đầu tiên là $\frac{1}{2}$, công sai là $-\frac{1}{2}.$

C. Số hạng đầu tiên là 0, công sai là $\frac{1}{2}$

D. Số hạng đầu tiên là 0, công sai là $-\frac{1}{2}.$

Câu 15. Dãy số nào sau đây không phải là cấp số nhân?

A. $1;2;4;8;\cdots$ .

B. $3;3^2;3^3;3^4;\cdots$ .

C. $4;2;\frac{1}{2};\frac{1}{4};\cdots$ .

D. $\frac{1}{\pi };\frac{1}{{\pi }^2};\frac{1}{{\pi }^4};\frac{1}{{\pi }^6};\cdots$ .

Câu 16. Cho cấp số nhân $\left(u_n\right)$ với $u_1=-2$ và $q=-5.$ Viết bốn số hạng đầu tiên của cấp số nhân.

A. $-2;10;50;-250.$

B. $-2;10;-50;250.$

C. $-2;-10;-50;-250.$

D. $-2;10;50;250.$

Câu 17. Bảng thống kê sau cho biết tốc độ (km/h) của một số xe máy khi đi qua vị trí có cảnh sát giao thông đang làm nhiệm vụ.

Quan sát mẫu số liệu trên và cho biết mệnh đề nào sau đây là đúng?

A. Số xe được đo tốc độ là 100 xe.

B. Mẫu số liệu đã cho gồm 5 nhóm có độ dài bằng nhau.

C. Tổng độ dài các nhóm là 80.

D. Số xe máy thuộc nhóm $\left(60;70\right)$ là ít nhất.

Câu 18. Điều tra về chiều cao của 100 học sinh lớp 10 trường THPT Lý Thường Kiệt, ta được kết quả:

Số học sinh có chiều cao từ 156 cm trở lên là

A. 37.

B. 77.

C. 12.

D. 25.

Câu 19. Cho bảng phân phối tần số ghép lớp:

Mệnh đề nào sau đúng là

A. Giá trị đại diện của lớp $\left(50;52\right)$là 53.

B. Tần số của lớp $\left(58;60\right)$là 95.

C. Tần số của lớp $\left(52;54\right)$là 35.

D. Số 50 không phụ thuộc lớp $\left(54;56\right)$.

Câu 20. Nhóm chứa mốt của mẫu số liệu trong Câu 19 là

A. $\left(54;56\right)$.

B. $\left(50;52\right)$.

C. $\left(52;54\right)$.

D. $\left(58;60\right)$.

Câu 21. Cho $\cos \alpha =\frac{4}{5}$ với $0<\alpha <\frac{\pi }{2}$. Tính $\sin \alpha$.

A. $\sin \alpha =\frac{1}{5}$.

B. $\sin \alpha =-\frac{1}{5}$.

C. $\sin \alpha =\frac{3}{5}$.

D. $\sin \alpha =\pm \frac{3}{5}$.

Câu 22. Rút gọn biểu thức $A=\frac{\sin x+\sin 2x+\sin 3x}{\cos x+\cos 2x+\cos 3x}$ .

A. $A=\tan 6x.$

B. $A=\tan 3x.$

C. $A=\tan 2x.$

D. $A=\tan x+\tan 2x+\tan 3x.$

Câu 23. Cho $\sin a=\frac{3}{5},\frac{\pi }{2}<a<\pi .$ Tính giá trị biểu thức $M=\sin \left(a+\frac{\pi }{4}\right)$.

A. $M=-\frac{\sqrt{2}}{10}$.

B. $M=-\frac{\sqrt{2}}{10}$.

C. $M=-\frac{\sqrt{2}}{10}$.

D. $M=-\frac{\sqrt{2}}{10}$.

Câu 24. Tìm giá trị lớn nhất Mvà giá trị nhỏ nhất mcủa hàm số $y=1-2\left(\text{cos}3x\right)$.

A. $M=3,m=-1$.

B. $M=0,m=-2$.

C. $M=1,m=-1$.

D. $M=2,m=-2$.

Câu 25. Hàm số $f\left(x\right)=2023\sin 3x$ tuần hoàn với chu kì bằng

A. $2\pi$.

B. $2023\pi$.

C. $\frac{2\pi }{2023}$.

D. $\frac{2\pi }{3}$.

Câu 26. Tất cả nghiệm của phương trình $\sin \left(x-\frac{\pi }{5}\right)=\sin \frac{2\pi }{5}$ là

A. $x=\frac{3\pi }{5}+k2\pi ,k\in \mathbb{Z}$ .

B. $x=\frac{4\pi }{5}+k2\pi ,k\in \mathbb{Z}$ .

C. $x=\frac{2\pi }{5}+k2\pi$ và $x=\frac{3\pi }{5}+k2\pi ,k\in \mathbb{Z}$ .

D. $x=\frac{3\pi }{5}+k2\pi$ và $x=\frac{4\pi }{5}+k2\pi ,k\in \mathbb{Z}$ .

Câu 27. Phương trình $\sin x=\cos x$ có số nghiệm thuộc đoạn $\left(-\pi ;\pi \right)$ là

A. 3.

B. 5.

C. 2.

D. 4.

Câu 28. Biết năm số hạng đầu của dãy số $\left(u_n\right)$ là $1,2,2,4,8,\mathrm{32...}$. Tìm một công thức truy hồi của dãy số trên.

A. $\left(\begin{array}{c}{u}_1=1;u_2=2\\ u_{n+2}=u_{n+1}.u_n\end{array}\right),\forall n\in {\mathbb{N}}^{*}$.

B. $\left(\begin{array}{c}{u}_1=1\\ u_{n+1}=2.u_n\end{array}\right),\forall n\in {\mathbb{N}}^{*}$.

C.$\left(\begin{array}{c}{u}_1=1\\ u_{n+1}=4u_n-2n\end{array}\right),\forall n\in {\mathbb{N}}^{*}$

D. $\left(\begin{array}{c}{u}_1=1;u_2=2\\ u_{n+2}=2u_{n+1}-2u_n\end{array}\right),\forall n\in {\mathbb{N}}^{*}$.

Câu 29. Cho dãy số $\left(u_n\right)$ được xác định bởi $\left(\begin{array}{c}{u}_1=2\\ u_{n+1}=3+u_n\end{array}\right),\forall n\in \left(1;2;3;4\right)$. Tìm công thức số hạng tổng quát của $\left(u_n\right)$.

A. $u_n=3n-1$ với $n\in \left(1;2;3;4;5\right)$.

B. $u_n=3n-1$ với $n\in \left(1;2;3;4\right)$.

C. $u_n=3^n$ với $n\in \left(1;2;3;4\right)$.

D. $u_n=2^n$ với $n\in \left(1;2;3;4;5\right)$.

Câu 30. Cho cấp số cộng $\left(u_n\right)$ biết $u_5=5$,$u_{10}=15$ . Khi đó $u_7$ bằng

A. $u_7=12$.

B. $u_7=8$.

C. $u_7=7$.

D. $u_7=9$.

Câu 31. Tổng của bao nhiêu số hạng đầu của cấp số cộng $1;-1;-3;\mathrm{...}$ bằng $-9800$ .

A. 100.

B. 99.

C. 101.

D. 98.

Câu 32. Cho cấp số nhân có các số hạng lần lượt là $x;12;y;192.$ Mệnh đề nào sau đây là đúng?

A. $x=1;y=144.$

B. $x=2;y=72.$

C. $x=3;y=48.$

D. $x=4;y=36.$

Câu 33. Cho cấp số nhân có các số hạng lần lượt là $3;9;27;81;\mathrm{...}$. Tìm số hạng tổng quát $u_n$ của cấp số nhân đã cho.

A. $u_n=3^{n-1}.$

B. $u_n=3^n.$

C. $u_n=3^{n+1}.$

D. $u_n=3+3^n.$

Câu 34. Tìm hiểu thời gian chạy cự li 1000 m (đơn vị: giây) của các bạn học sinh trong một lớp thu được kết quả sau:

Thời gian (giây) chạy trung bình cự li 1000 m của các bạn học sinh là

A. $130,35$.

B. $131,03$.

C. $130,4$.

D. $132,5$.

Câu 35.Trung vị của mẫu số liệu ghép nhóm trong Câu 34 là

A. $M_e=\frac{392}{3}$.

B. $M_e=\frac{394}{3}$.

C. $M_e=\frac{391}{3}$.

D. $M_e=\frac{395}{3}$.

II. Tự luận (3 điểm)

Bài 1. (1 điểm) Tìm m để hàm số $y=\sqrt{2{\sin }^{2}x+4\sin x\cos x-\left(3+2m\right){\cos }^{2}x+2}$ xác định với mọi x.

Bài 2. (1 điểm) Một hãng taxi áp dụng mức giá đối với khách hàng theo hình thức bậc thang như sau: Mỗi bậc áp dụng cho 10 km. Bậc 1 (áp dụng cho 10 km đầu) có giá trị 10 000 đồng/1 km, giá mỗi km ở các bậc tiếp theo giảm 5% so với giá của bậc trước đó. Bạn An thuê hãng taxi đó để đi quãng đường 114 km, nhưng khi đi được 50 km thì bạn Bình đi chung hết quãng đường còn lại. Tính số tiền mà bạn An phải trả, biết rằng mức giá áp dụng từ lúc xe xuất phát và số tiền trên quãng đường đi chung bạn An chỉ phải trả 20% (Kết quả làm tròn đến hàng nghìn).

Bài 3. (1 điểm)Tìm hiểu thời gian hoàn thành một bài tập (đơn vị: phút) của một số học sinh thu được kết quả sau:

Hãy cho biết ngưỡng thời gian để xác định 25% học sinh hoàn thành bài tập với thời gian lâu nhất.

-----HẾT-----

ĐÁP ÁN ĐỀ SỐ 1

I. Bảng đáp án trắc nghiệm

II. Đáp án tự luận

Bài 1. Với $m\le -1$ thì thỏa mãn yêu cầu bài toán.

Bài 2. Số tiền bạn An cần trả là 539 000 (đồng).

Bài 3. Ngưỡng thời gian cần tìm là 14 phút.

Đề thi giữa kì 1 Toán 11 Kết nối tri thức có đáp án - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Giữa kì 1 - Kết nối tri thức

Năm học 2024 - 2025

Môn: Toán lớp 11

Thời gian làm bài: phút

(Đề số 2)

Phần trắc nghiệm (4 điểm)

Câu 1: Góc lượng giác có số đo $\alpha$ thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau:

A. $\alpha +k{180}^{\circ }$	B. $\alpha +k{360}^{\circ }$
C. $\alpha +k2\pi$	D. $\alpha +k\pi$

Câu 2: Biết $\tan x=\frac{1}{2}$, giá trị của biểu thức $M=\frac{2{\sin }^{2}x+3\sin x.\cos x-4{\cos }^{2}x}{5{\cos }^{2}x-{\sin }^{2}x}$ bằng:

A. $-\frac{8}{13}$	B. $\frac{2}{19}$
C. $-\frac{2}{19}$	D. $-\frac{8}{19}$

Câu 3: Mệnh đề nào sau đây đúng?

A. $\tan \left(x-y\right)=\frac{\tan x+\tan y}{\tan x\tan y}$.

B. $\tan \left(x-y\right)=\frac{\tan x-\tan y}{1+\tan x\tan y}$.

C. $\tan \left(x-y\right)=\frac{\tan x-\tan y}{1-\tan x\tan y}$.

D. $\tan \left(x-y\right)=\frac{\tan x-\tan y}{\tan x\tan y}$.

Câu 4: Công thức nào sau đây là sai?

A. $\cos a+\cos b=2\cos \frac{a+b}{2}.\cos \frac{a-b}{2}$.

B. $\cos a-\cos b=-2\sin \frac{a+b}{2}.\sin \frac{a-b}{2}$.

C. $\sin a+\sin b=2\sin \frac{a+b}{2}.\cos \frac{a-b}{2}$.

D. $\sin a-\sin b=2\sin \frac{a+b}{2}.\cos \frac{a-b}{2}$.

Câu 5: Cho các hàm số: $y=\cos x$, $y=\tan x$, $y=\cot x$. Có bao nhiêu hàm số tuần hoàn với chu kỳ $T=\pi$.

A. 1	B. 2
C. 3	D. 4

Câu 6: Gọi $M$ và $m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=\cos 2x+\cos x.$ Khi đó $M+m$bằng bao nhiêu?

A. $M+m=\frac{7}{8}$	B. $M+m=\frac{8}{7}$
C. $M+m=\frac{9}{8}$	D. $M+m=\frac{9}{7}$

Câu 7: Nghiệm của phương trình $\cos \left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}$ là:

A. $[\begin{array}{l}x=k2\pi \\ x=-\frac{\pi }{2}+k\pi \end{array}\left(k\in \mathbb{Z}\right)$	B. $[\begin{array}{l}x=k\pi \\ x=-\frac{\pi }{2}+k\pi \end{array}\left(k\in \mathbb{Z}\right)$
C. $[\begin{array}{l}x=k\pi \\ x=-\frac{\pi }{2}+k2\pi \end{array}\left(k\in \mathbb{Z}\right)$	D. $[\begin{array}{l}x=k2\pi \\ x=-\frac{\pi }{2}+k2\pi \end{array}\left(k\in \mathbb{Z}\right)$

Câu 8: Số nghiệm của phương trình $\cos x=\frac{1}{2}$ thuộc đoạn $\left[-2\pi ;2\pi \right]$ là:

A. 4	B. 2
C. 3	D. 1

Câu 9: Cho dãy số có các số hạng đầu là:$5;10;15;20;25;...$ Số hạng tổng quát của dãy số này là:

A. $u_n=5(n-1)$	B. $u_n=5n$
C. $u_n=5+n$	D. $u_n=5.n+1$

Câu 10: Cho dãy số $SC$, biết $AD$. Ba số hạng đầu tiên của dãy số là:

A. $\left(\alpha \right)$	B. $S.ABCD$
C. $M$	D. $SA$

Câu 11: Trong các dãy số sau, dãy số nào là một cấp số cộng?

A. $1;-2;-4;-6;-8$	B. $1;-3;-6;-9;-12.$
C. $1;-3;-7;-11;-15.$	D. $1;-3;-5;-7;-9$

Câu 12: Xác định số hàng đầu $u_1$ và công sai $d$ của cấp số cộng $\left(u_n\right)$ có $u_9=5u_2$ và $u_{13}=2u_6+5$.

A. $u_1=3$ và $d=4$	B. $u_1=3$ và $d=5$
C. $u_1=4$ và $d=5$	D. $u_1=4$ và $d=3$

Câu 13: Cho cấp số cộng $\left(u_n\right)$ thỏa $\{\begin{array}{l}{u}_2-u_3+u_5=10\\ u_4+u_6=26\end{array}$. Tính $S=u_1+u_4+u_7+...+u_{2011}$

A. $S=2023736$	B. $S=2023563$
C. $S=6730444$	D. $S=6734134$

Câu 14: Dãy số nào sau đây không phải là cấp số nhân?

A. $1;-3;9;-27;54$	B. $1;2;4;8;16$
C. $1;-1;1;-1;1$	D. $1;-2;4;-8;16$

Câu 15: Cho cấp số nhân $\left(u_n\right)$ biết $\{\begin{array}{l}{u}_4-u_2=54\\ u_5-u_3=108\end{array}$. Tìm số hạng đầu $u_1$ và công bội $q$ của cấp số nhân trên.

A. $u_1=9$; $q=2$	B. $u_1=9$; $q=-2$
C. $u_1=-9$; $q=-2$	D. $u_1=-9$; $q=2$

Câu 16: Giá trị của tổng $4+44+444+...+\mathrm{44...4}$ bằng:

A. $\frac{40}{9}\left({10}^{2018}-1\right)+2018$	B. $\frac{4}{9}\left(\frac{{10}^{2019}-10}{9}-2018\right)$
C. $\frac{4}{9}\left(\frac{{10}^{2019}-10}{9}+2018\right)$	D. $\frac{4}{9}\left({10}^{2018}-1\right)$

Câu 17: Khảo sát thời gian tập thể dục trong ngày của một số học sinh khối 11 thu được mẫu số liệu ghép nhóm sau:

 

Giá trị đại diện của nhóm $[20;40)$ là:

A. 10	B. 20
C. 30	D. 40

Câu 18: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

 

Số trung bình của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

A. $\left[7;9\right)$	B. $\left[9;11\right)$
C. $\left[11;13\right)$	D. $\left[13;15\right)$

Câu 19: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

 

Tứ phân vị thứ nhất của mẫu số liệu trên gần nhất với giá trị nào trong các giá trị sau?

A. 7	B. 7,6
C. 8	D. 8,6

Câu 20: Doanh thu bán hàng trong 20 ngày được lựa chọn ngã̃u nhiên của một cửa hàng được ghi lại ở bảng sau (đơn vị: triệu đồng):

 

Trung vị của mẫu số liệu trên thuộc khoảng nào trong các khoảng dưới đây?

A. $\left[7;9\right)$	B. $\left[9;11\right)$
C. $\left[11;13\right)$	D. $\left[13;15\right)$

Phần tự luận (6 điểm)

Bài 1. ( 1 điểm)

Tìm giá trị lớn nhất và giá trị nhỏ nhất : $y=4{\cos }^{2}x-4\cos x+3$  với $x\in \left[\frac{\pi }{3};\frac{5\pi }{6}\right]$.

Bài 2. ( 1.5 điểm)

a) Giải phương trình $\sin \left(\frac{x}{2}-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{4}$

b) Tìm nghiệm thuộc khoảng $\left(-\frac{\pi }{4};2\pi \right)$ của phương trình $\sin \left(\frac{\pi }{6}+2x\right)=-1$.

c) Giải phương trình sau: $\cos x+\cos 2x+\cos 3x=0$.

Bài 3. ( 2 điểm)

a) Cho cấp số cộng $\left(u_n\right)$có $u_1=-2$ và $d=3$. Biết $S_n=6095374$, tìm $n$.

b) Tìm số hạng đầu tiên và công bội của cấp số nhân sau, biết rằng: $\{\begin{array}{l}{u}_1+u_5=51\\ u_2+u_6=102\end{array}$.

Bài 4. ( 1,5 điểm)

Ghi lại tốc độ bóng trong 200 lần giao bóng của một vận động viên môn quần vợt cho kết quả như bảng bên.

a) Tính trung vị của mẫu số liệu ghép nhóm này.

b) Tìm tứ phân vị thứ nhất và tứ phân vị thứ ba của mẫu số liệu ghép nhóm này.

-------- Hết --------

ĐÁP ÁN

Phần trắc nghiệm (4 điểm)

Câu 1: 

Góc lượng giác có số đo $\alpha$ thì mọi góc lượng giác cùng tia đầu và tia cuối với nó có số đo dạng nào trong các dạng sau: $\alpha +k2\pi$.

Đáp án C

Câu 2: 

Ta có: $\tan x=\frac{1}{2}\iff \frac{\sin x}{\cos x}=\frac{1}{2}\iff \cos x=2\sin x$.

Khi đó $M=\frac{2{\sin }^{2}x+3\sin x.2\sin x-4.{\left(2\sin x\right)}^2}{5.{\left(2\sin x\right)}^2-{\sin }^{2}x}=\frac{-8{\sin }^{2}x}{19{\sin }^{2}x}=-\frac{8}{19}$.

Đáp án D

Câu 3: 

Ta có: $\tan \left(x-y\right)=\frac{\tan x-\tan y}{1+\tan x\tan y}$.

Đáp án B

Câu 4: 

Ta có: $\sin a-\sin b=2\cos \frac{a+b}{2}.\sin \frac{a-b}{2}$.

Đáp án D

Câu 5: 

Hàm số $y=\tan x$, $y=\cot x$ là hàm số tuần hoàn với chu kỳ $T=\pi$.

Hàm số $y=\cos x$ là hàm số tuần hoàn với chu kỳ $T=2\pi$.

Đáp án B

Câu 6: 

TXĐ : $D=\mathbb{R}$.

Ta có: $y=\cos 2x+\cos x=2{\cos }^2+\cos x-1$.

Đặt : $t=\cos x$, $t\in \left[-1;1\right]$.

Xét$f\left(t\right)=2t^2+t-1$.

Đồ thị của hàm số $f$ là parabol có đỉnh $I\left(-\frac{1}{4};-\frac{9}{8}\right)$.

BBT:

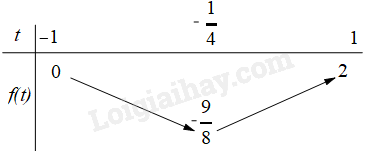
Dựa vào BBT ta có : $M=\underset{\left[-1;1\right]}{max}f\left(t\right)=2$, $m=\underset{\left[-1;1\right]}{min}f\left(t\right)=-\frac{9}{8}$.

Vậy $M+m=\frac{7}{8}$.

Đáp án A

Câu 7: 

Phương trình $\cos \left(x+\frac{\pi }{4}\right)=\frac{\sqrt{2}}{2}\iff \cos \left(x+\frac{\pi }{4}\right)=\cos \left(\frac{\pi }{4}\right)\Rightarrow [\begin{array}{l}x=k2\pi \\ x=-\frac{\pi }{2}+k2\pi \end{array}\left(k\in \mathbb{Z}\right)$.

Đáp án D

Câu 8: 

Ta có: $\cos x=\frac{1}{2}$$\iff$$[\begin{array}{l}x=\frac{\pi }{3}+k2\pi \\ x=-\frac{\pi }{3}+k2\pi \end{array}$, $k\in \mathbb{Z}$.

Xét $x=\frac{\pi }{3}+k2\pi$, do $x\in \left[-2\pi ;2\pi \right]$ và $k\in \mathbb{Z}$ nên $-2\pi \le \frac{\pi }{3}+k2\pi \le 2\pi$$\Rightarrow k=-1$; $k=0$.

Xét $x=-\frac{\pi }{3}+k2\pi$, do $x\in \left[-2\pi ;2\pi \right]$ và $k\in \mathbb{Z}$ nên $-2\pi \le -\frac{\pi }{3}+k2\pi \le 2\pi$$\Rightarrow k=1$; $k=0$.

Vậy phương trình có $4$ nghiệm trên đoạn $\left[-2\pi ;2\pi \right]$.

Đáp án A

Câu 9: 

Ta có:

$5=5.1$

$10=5.2$

$15=5.3$

$20=5.4$

$25=5.5$

Suy ra số hạng tổng quát $u_n=5n$.

Đáp án B

Câu 10: 

Ta có: $u_1=\frac{1}{2^1-1}=1;u_2=\frac{2}{2^2-1}=\frac{2}{3};u_3=\frac{3}{2^3-1}=\frac{3}{7}$.

Đáp án D

Câu 11: 

Ta thấy dãy số: $1;-3;-7;-11;-15$ là một cấp số cộng có số hạng đầu là 1 và công sai bằng $-4.$

Đáp án C

Câu 12: 

Ta có: $u_n=u_1+\left(n-1\right)d$.

Theo đầu bài ta có hpt: $\{\begin{array}{l}{u}_1+8d=5\left(u_1+d\right)\\ u_1+12d=2\left(u_1+5d\right)+5\end{array}$$\iff \{\begin{array}{l}4u_1-3d=0\\ u_1-2d=-5\end{array}\iff \{\begin{array}{l}{u}_1=3\\ d=4\end{array}$.

Đáp án A

Câu 13: 

Ta có: $\{\begin{array}{l}{u}_2-u_3+u_5=10\\ u_4+u_6=26\end{array}$$\iff \{\begin{array}{l}{u}_1+d-u_1-2d+u_1+4d=10\\ u_1+3d+u_1+5d=26\end{array}$$\iff \{\begin{array}{l}{u}_1+3d=10\\ 2u_1+8d=26\end{array}$$\iff \{\begin{array}{l}{u}_1=1\\ d=3\end{array}$.

Ta có: $u_1$, $u_4$, $u_7$, $u_{10}$, …,$u_{2011}$ là cấp số cộng có $\{\begin{array}{l}{u}_1=1\\ d=9\\ n=671\end{array}$

Do đó: $S=\frac{671}{2}\left(2.1+670.9\right)=2023736$.

Đáp án A

Câu 14: 

Dãy $1;2;4;8;16$ là cấp số nhân với công bội $q=2$.

Dãy $1;-1;1;-1;1$ là cấp số nhân với công bội $q=-1$.

Dãy $1;-2;4;-8;16$ là cấp số nhân với công bội $q=-2$.

Dãy $1;-3;9;-27;54$ không phải là cấp số nhân vì $-3=1.(-3);(-27).(-3)=81\ne 54$.

Đáp án A

Câu 15: 

Ta có : $\{\begin{array}{l}{u}_4-u_2=54\\ u_5-u_3=108\end{array}$$\iff \{\begin{array}{l}{u}_1{q}^3-u_{1}q=54\\ u_1{q}^4-u_1{q}^2=108\end{array}$$\iff \{\begin{array}{l}{u}_{1}q\left(q^2-1\right)=54\\ u_1{q}^2\left(q^2-1\right)=108\end{array}$$\iff \{\begin{array}{l}{u}_1=9\\ q=2\end{array}$.

Vậy $u_1=9$; $q=2$.

Đáp án A

Câu 16: 

Đặt $S=4+44+444+...+\mathrm{44...4}$.

Ta có:$\frac{9}{4}S=9+99+999+...+\mathrm{99...9}$$=\left(10-1\right)+\left({10}^2-1\right)+\left({10}^3-1\right)+...\left({10}^{2018}-1\right)$

Suy ra: $\frac{9}{4}S=$$\left(10+{10}^2+{10}^3+...+{10}^{2018}\right)-2018$.

Đặt $A=10+{10}^2+{10}^3+...+{10}^{2018}$.

Ta có: $A=10+{10}^2+{10}^3+...+{10}^{2018}$ là tổng $2018$ số hạng của một cấp số nhân có số hạng đầu $u_1=10$, công bội $q=10$ nên ta có $A=u_1\frac{1-q^{2018}}{1-q}$$=10\frac{1-{10}^{2018}}{-9}$$=\frac{{10}^{2019}-10}{9}$.

Do đó $\frac{9}{4}S=\frac{{10}^{2019}-10}{9}-2018$$\iff S=\frac{4}{9}\left(\frac{{10}^{2019}-10}{9}-2018\right)$.

Đáp án B

Câu 17: 

Giá trị đại diện của nhóm $[20;40)$ là: $\frac{20+40}{2}=30$.

Đáp án C

Câu 18: 

Số trung bình của mẫu số liệu xấp xỉ bằng: $\left(6.2+8.7+10.7+12.3+14.1\right):20=9,4$

Đáp án B

Câu 19: 

Tứ phân vị thứ nhất của dãy số liệu là $\frac{1}{2}\left(x_4+x_5\right)$ thuộc nhóm $\left[7;9\right)$ nên tứ phân vị thứ nhất của mẫu số liệu là $Q_1=7+\frac{\frac{20}{4}-2}{7}\left(9-7\right)=7,86$.

Đáp án B

Câu 20: 

Gọi $x_1;x_2;x_3;\dots ;x_{20}$ lần lượt là thời gian chạy của các vận động viên theo thứ tự từ nhỏ đến lớn.

Do $x_1,x_2\in \left[5;7\right);x_3,\dots ,x_9\in \left[7;9\right);x_{10},\dots ,x_{16}\in \left[9;11\right);x_{17},\dots ,x_{19}\in \left[11;13\right)$; $x_{20}\in \left[13;15\right)$.

Trung vị của mẫu số liệu là $x_{10},\dots ,x_{16}$ thuộc nhóm $\left[9;11\right)$.

Đáp án B

Phần tự luận.

Bài 1. ( 1 điểm)

Đặt $t=\cos x$.

Với $\frac{\pi }{3}\le x\le \frac{5\pi }{6}$ ta có $\frac{-\sqrt{3}}{2}\le t\le \frac{1}{2}$ .

Khi đó ta có $y=f\left(t\right)=4t^2-4t+3$ , $\frac{-\sqrt{3}}{2}\le t\le \frac{1}{2}$.

Ta có bảng biến thiên:

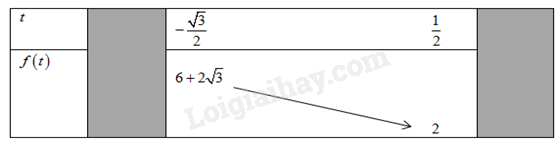
Từ bảng biến thiên ta có:

Giá trị lớn nhất của hàm số đã cho trên $\left[\frac{\pi }{3};\frac{5\pi }{6}\right]$ là $6+2\sqrt{3}$.

Giá trị nhỏ nhất của hàm số đã cho trên $\left[\frac{\pi }{3};\frac{5\pi }{6}\right]$ là $2$.

Bài 2. (1.5 điểm)

a) Ta có: $\sin \left(\frac{x}{2}-\frac{\pi }{3}\right)=-\frac{\sqrt{3}}{4}$ đặt $\sin t=-\frac{\sqrt{3}}{4}$

$$\begin{gathered} \Rightarrow \sin \left(\frac{x}{2}-\frac{\pi }{3}\right)=\sin t \\ \Rightarrow [\begin{array}{c}\frac{x}{2}-\frac{\pi }{3}=t+k2\pi \\ \frac{x}{2}-\frac{\pi }{3}=\pi -t+k2\pi \end{array} \\ \iff [\begin{array}{c}x=\frac{2\pi }{3}+2t+k4\pi \\ x=\frac{8\pi }{3}-2t+k4\pi \end{array} \end{gathered}$$.

b) Ta có:

$$\begin{gathered} \sin \left(\frac{\pi }{6}+2x\right)=-1 \\ \iff \frac{\pi }{6}+2x=-\frac{\pi }{2}+k2\pi \\ \iff x=-\frac{\pi }{3}+k\pi \end{gathered}$$

Theo để bài, ta có: $-\frac{\pi }{4}<-\frac{\pi }{3}+k\pi <2\pi \Rightarrow k=1;2\Rightarrow x=\frac{2\pi }{3};\frac{5\pi }{3}.$

c) Ta có: $\cos x+\cos 2x+\cos 3x=0$

$\iff 2\cos \left(\frac{x+3x}{2}\right).\cos \left(\frac{x-3x}{2}\right)+\cos 2x=0$

$\iff 2\cos 2x.\cos x+\cos 2x=0$

$\iff \cos 2x\left(2\cos x+1\right)=0$

$\iff [\begin{array}{l}\cos 2x=0\\ \cos x=\frac{1}{2}\end{array}\iff [\begin{array}{l}x=\frac{\pi }{4}+k\frac{\pi }{2}\\ x=\frac{2\pi }{3}+k2\pi \\ x=-\frac{2\pi }{3}+k2\pi \end{array}$.

Bài 3. (2 điểm)

a) Ta có : 

$$\begin{gathered} S_n=n{u}_1+\frac{n\left(n-1\right)}{2}d \\ =-2n+\frac{3\left(n^2-n\right)}{2}=\frac{n\left(3n-7\right)}{2} \end{gathered}$$

Vì $S_n=6095374$ nên $\frac{n\left(3n-7\right)}{2}=6095374\iff 3n^2-7n-12190748=0\iff [\begin{array}{l}n=2017\\ n=-\frac{6044}{3}\end{array}$.

Vậy $n=2017$.

b) Ta có :

$$\begin{gathered} \{\begin{array}{l}{u}_1+u_5=51\\ u_2+u_6=102\end{array}\iff \{\begin{array}{l}{u}_1+u_1{q}^4=51\\ u_{1}q+u_1{q}^5=102\end{array} \\ \iff \{\begin{array}{l}{u}_1\left(1+q^4\right)=51(\ast )\\ u_{1}q\left(1+q^4\right)=102\left(\ast \ast \right)\end{array} \end{gathered}$$

Lấy$\frac{\left(\ast \ast \right)}{(\ast )}\iff \frac{u_{1}q\left(1+q^4\right)}{u_1\left(1+q^4\right)}=\frac{102}{51}$ $\iff q=2\Rightarrow u_1=\frac{51}{1+q^4}=\frac{51}{17}=3.$

Kết luận có công bội $q=2$và số hạng đầu tiên $u_1=3$.

Bài 4. ( 1.5 điểm)

a) Cỡ mẫu là: $n=18+28+35+43+43+41+35=200$.

Gọi $x_1,x_2\dots x_{200}$ là tốc độ giao bóng của 200 lần và giả sử dãy này được sắp xếp theo thứ tự tăng dần. Khi đó trung vị là $\frac{x_{100}+x_{101}}{2}$.

Do hai giá trị $x_{100},x_{101}$ thuộc nhóm [165;170) nên nhóm này chứa trung vị.

Suy ra, $p=4;a_4=165;m_4=43;m_1+m_2+m_3=18+28+35=81;a_5-a_4=5$ và ta có:

$M_e=165+\frac{\frac{200}{2}-81}{43}\times 5=167,21$.

b) Cỡ mẫu: $n=200$.

Tứ phân vị thứ nhất $Q_1$ là $\frac{x_{50}+x_{51}}{2}$. Do $x_{50};x_{51}$ đều thuộc nhóm [160;165) nên tứ phân vị thứ nhất thuộc nhóm [160;165). Do đó, $p=3;a_3=160;m_3=35;m_1+m_2=18+28=46;a_4-a_3=5$ và ta có:

$Q_1=160+\frac{\frac{200}{4}-46}{35}\times 5=160,57$.

Tứ phân vị thứ ba $Q_3$ là $\frac{x_{150}+x_{151}}{2}$. Do $x_{150},x_{151}$ đều thuộc nhóm [170;175) nên tứ phân vị thứ ba thuộc nhóm [170;175). Do đó,$p=5;a_5=170;m_5=41;m_1+m_2+m_3+m_4=18+28+35+43=124;a_6-a_5=5$

và ta có:

$Q_3=170+\frac{\frac{600}{4}-124}{41}\times 5=173,17$.