Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Chuyên đề luyện thi vào lớp 10 phần Hình học, tài liệu bao gồm 119 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Tài liệu gồm có:
I. Lý thuyết
CÁC KÍ HIỆU DÙNG TRONG CHUYÊN ĐỀ
(O) : Đường tròn tâm O
(O;R) : Đường tròn tâm O, bán kính R
ABC : Tam giác ABC
\({S_{ABC}}\): Diện tích \(\Delta ABC\)
(ABC) : Đường tròn ngoại tiếp \(\Delta ABC\)
a, b, c : Độ dài các cạnh đối diện với các đỉnh A, B, C của \(\Delta ABC\)
\({h_a},{h_b},{h_c}\) : Độ dài các đường cao xuất phát từ các đỉnh A, B, C của \(\Delta ABC\)
\({m_a},{m_b},{m_c}\) : Độ dài các đường trung tuyến xuất phát từ các đỉnh A, B, C của \(\Delta ABC\)
\({l_a},{l_b},{l_c}\) : Độ dài các đường phân giác xuất phát từ các đỉnh A, B, C của \(\Delta ABC\)
R, r : Bán kính các đường tròn ngoại tiếp, nội tiếp tam giác
\({r_a},{r_b},{r_c}\) : Bán kính các đường tròn bàng tiếp đối diện với các đỉnh A, B, C của \(\Delta ABC\)
đpcm : Điều phải chứng minh
2p : Chu vi của tam giác (\(p = \frac{{a + b + c}}{2}\) là nửa chu vi)
\(\sum\limits_{k - 1}^n {{a_k} = {a_1} + {a_2} + ... + {a_n}} \) : Tổng của n số hạng từ \({a_1}\) đến \({a_n}\).
\(\prod\limits_{k - 1}^n {{a_k} = {a_1}{a_2}...{a_n}} \) : Tích của n số hạng từ \({a_1}\)đến \({a_n}\).
TỔNG KẾT KIẾN THỨC
1. Đường thẳng:
Định nghĩa: Một đường thẳng được hiểu như là một đường dài (vô tận), mỏng (vô cùng) và thẳng tuyệt đối.
Tiên đề Ơ’Clit: Qua hai điểm bất kì ta luôn xác định duy nhất một đường thẳng và chỉ một đường thẳng.
Kí hiệu: Người ta thường dùng các chữ cái in thường a, b, c,…, m, n, p… để đặt tên cho các đường thẳng hoặc dùng hai chữ cái in hoa hay hai chữ cái in thường để đặt tên cho đường thẳng.
Ví dụ:

Điểm không thuộc đường thẳng: Điểm A không nằm trên đường thẳng a, điểm A không thuộc đường thẳng a (hay nói cách khác là đường thẳng a không đi qua điểm A).
Kí hiệu: \(A \notin a\).
2. Đoạn thẳng:
Định nghĩa: Đoạn thẳng AB là hình gồm điểm A, điểm B và tất cả các điểm nằm giữa A và B.
![]()
Hai điểm A và B gọi là hai đầu mút (hay còn gọi là hai mút) của đoạn thẳng AB.
Lưu ý:
Điểm M nằm giữa A và B khi và chỉ khi AM + MB = AB và A, M, B thẳng hàng.
![]()
3. Tia:
Tia là hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O (có hai tia Ox và Oy như hình vẽ).
![]()
Hai tia có chung một góc O tạo thành đường thẳng được gọi hai tia đối nhau (hai tia Ox và Oy trong hình vẽ là hai tia đối nhau)
4. Điểm:
Để kí hiệu điểm, người ta dùng các chữ cái in hoa A, B, C,…
Bất cứ hình nào cũng là một tập hợp các điểm.
Trung điểm của đoạn thẳng: Trung điểm M của đoạn thẳng AB là điểm nằm giữa hai điểm A, B và cách đều hai điểm A và B.
![]()
Trung điểm M của đoạn thẳng AB còn gọi là điểm chính giữa của đoạn thẳng AB.
Lưu ý:
Điểm chính giữa hai điểm khác với điểm nằm giữa hai điểm.
5. Mặt phẳng:
Nửa mặt phẳng bờ a: Hình gồm đường thẳng a và một phần mặt phẳng bị chia ra bởi a được gọi là một nửa mặt phẳng bờ a.

Mặt phẳng là hai nửa mặt phẳng hợp lại theo một phương (phương của vectơ) nhất định.
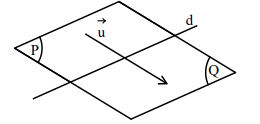
6. Góc:
(1) Hai góc phụ nhau là hai góc có tổng số đo bằng 900.
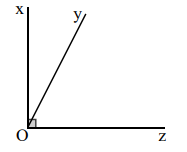
Góc \(\widehat {xOy}\) và góc \(\widehat {yOz}\) là hai góc phụ nhau.
(2) Hai góc bù nhau là hai góc có tổng số đo bằng 1800.
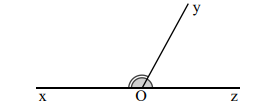
Góc \(\widehat {xOy}\) và góc \(\widehat {yOz}\) là hai góc bù nhau
(3) Hai góc so le trong: Cho hai đường thẳng a // b và đường thẳng c cắt a,b lần lượt tại A, B.
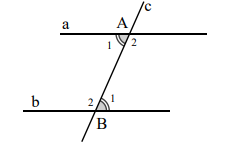
Khi đó:
\(\widehat {{A_1}} = \widehat {{B_1}}\) và \(\widehat {{A_2}} = \widehat {{B_2}}\).
(4) Hai góc đồng vị: Cho hai đường thẳng a // b và đường thẳng c cắt a, b lần lượt tại A, B. Khi đó:
\(\widehat {{A_1}} = \widehat {{B_1}}\), \(\widehat {{A_2}} = \widehat {{B_2}}\), \(\widehat {{A_3}} = \widehat {{B_3}}\), \(\widehat {{A_4}} = \widehat {{B_4}}\).
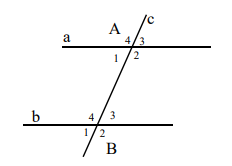
7. Tam giác:
7.1. Kí hiệu:
Tam giác ABC được kí hiệu là \(\Delta ABC\).
Một tam giác ABC có ba đỉnh (góc) lần lượt là A, B, C và ba cạnh là AB, BC, CA.
7.2. Các đường trong tam giác:
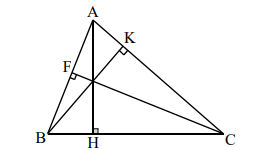
Đường cao: Là đoạn thẳng nối mỗi đỉnh và vuông góc với cạnh đối diện đỉnh đó. Một tam giác có ba đường cao. Giao điểm của ba đường cao gọi là trực tâm của tam giác.
Trong \(\Delta ABC\), có các đường cao AH, BK, CF.
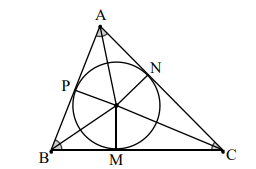
Đường trung tuyến: Là đường thẳng kẻ từ đỉnh và đi qua trung điểm của cạnh đối diện với đỉnh đó. Một tam giác có ba đường trung tuyến. Giao điểm của ba đường trung tuyến gọi là trọng tâm của tam giác.
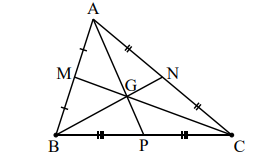
Trong \(\Delta ABC\), có các đường trung tuyến AP, BN, CM.
Độ dài đường trung tuyến:
\(\frac{{BG}}{{BN}} = \frac{{AG}}{{AP}} = \frac{{CG}}{{CM}} = \frac{2}{3}\)
\(\frac{{GN}}{{BN}} = \frac{{GP}}{{AP}} = \frac{{GM}}{{CM}} = \frac{1}{3}\)
\(\frac{{GN}}{{GB}} = \frac{{GP}}{{GA}} = \frac{{GM}}{{GC}} = \frac{1}{2}\)
Đường trung trực: Là đường thẳng vuông góc với một cạnh tại trung điểm của nó. Một tam giác có ba đường trung trực. Giao điểm của ba đường trung trực gọi là tam của đường trong ngoại tiếp tam giác.
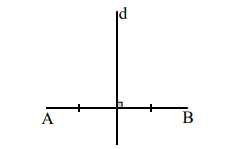
Đường thẳng (d) là đường trung trực của đoạn thẳng AB.
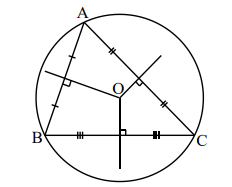
Điểm O là giao điểm của ba đường trung trực.
Đường phân giác: Là đường thẳng chia một góc thành hai góc có số đo bằng nhau. Một tam giác có ba đường phân giác. Giao điểm của ba đường phân giác gọi là tâm của đường trong nội tiếp tam giác.
Trong \(\Delta ABC\) có: OM = ON = OP
Đường trung bình: Là đường thẳng nối trung điểm hai cạnh của một tam giác. Một tam giác có ba đường trung bình. Tam giác tạo bởi ba đường trung bình thì đồng dạng với tam giác đã cho.
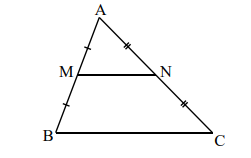
MN gọi là đường trung bình của tam giác.
Ta có: MN // BC và \(MN = \frac{1}{2}BC\).
7.3. Phân loại tam giác:
Tam giác nhọn: Là tam giác có ba góc đều nhọn (số đo ba góc < 900)