Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu 30 Đề thi học sinh giỏi Toán lớp 7, tài liệu bao gồm 30 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tóm tắt tài liệu

30 đề học sinh giỏi toán 7

Đề thi học sinh giỏi toán lớp 7

Đề số 1:

Thời gian làm bài 120 phút

Bài 1. Tìm giá trị n nguyên dương:

a) \(\frac{1}{8}{.16^n} = {2^n}\);

b) 27<3ⁿ<243

Bài 2. Thực hiện phép tính:

\((\frac{1}{{4.9}} + \frac{1}{{9.14}} + \frac{1}{{14.19}} + ... + \frac{1}{{44.49}})\frac{{1 - 3 - 5 - 7 - ... - 49}}{{89}}\)

Bài 3. a) Tìm x biết: |2x+3|=x+2

b) Tìm giá trị nhỏ nhất của A =|x – 2006|+|2007 – x|. Khi x thay đổi

Bài 4. Hiện nay hai kim đồng hồ chỉ 10 giờ. Sau ít nhất bao lâu thì 2 kim đồng hồ nằm đối diện nhau trên một đường thẳng.
Bài 5. Cho tam giác vuông ABC ( A = 1v), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE = BC.

Đề số 2:

Đề thi học sinh giỏi

Môn toán lớp 7

Thời gian làm bài 120 phút

Bài 1: (4 điểm)

a) Thực hiện phép tính:

\(A = \frac{{{2^{12}}{{.3}^5} - {4^8}{{.9}^2}}}{{{{({2^2}.3)}^6} + {8^4}{{.3}^5}}} - \frac{{{5^{10}}{{.7}^3} - {{25}^5}{{.49}^2}}}{{{{(125.7)}^3} + {5^9}{{.14}^3}}}\)

b) Chứng minh rằng: Với mọi số nguyên dương n thỡ:

3ⁿ⁺² – 2ⁿ⁺² + 3ⁿ – 2ⁿ chia hết cho 10

Bài 2: (4 điểm)

Tìm x biết:

a. \(|x - \frac{1}{3}| + \frac{4}{5} = |( - 3,2) + \frac{2}{5}|\)

b. (x – 7)^x+1 – (x – 7)^x+11=0

Bài 3: (4 điểm)
Số A được chia thành 3 số tỉ lệ theo \(\frac{2}{5};\frac{3}{4};\frac{1}{6}.\) Biết rằng tổng các bình phương của ba số đó bằng 24309. Tìm số A.

a) Cho \(\frac{a}{c} = \frac{c}{b}\). Chứng minh rằng: \(\frac{{{a^2} + {c^2}}}{{{b^2} + {c^2}}} = \frac{a}{b}\)

 Bài 4: (4 điểm)
Cho tam giác ABC, M là trung điểm của BC. Trên tia đối của của tia MA lấy điểm E sao cho
ME = MA. Chứng minh rằng:
a) AC = EB và AC // BE
b) Gọi I là một điểm trên AC ; K là một điểm trên EB sao cho AI = EK . Chứng minh
ba điểm I , M , K thẳng hàng
c) Từ E kẻ \(EH \bot BC(H \in BC).\)Biết \(\widehat {HBE} = {50^0};\widehat {MEB} = {25^0}.\)Tính \(\widehat {HEM}\)và \(\widehat {BME}\)

Bài 5: (4 điểm)
Cho tam giác ABC cân tại A có \(\widehat A = {20^0}\), vẽ tam giác đều DBC (D nằm trong tam giác ABC).
Tia phân giác của góc ABD cắt AC tại M. Chứng minh:
a) Tia AD là phân giác của góc BAC
b) AM = BC
Đáp án đề 1toán 7

Bài 1. Tìm giá trị n nguyên dương: (4 điểm mỗi câu 2 điểm)

a) \(\frac{1}{8}{.16^n} = {2^n};\) => 2^4n-3=2ⁿ => 4n – 3 = n => n=1

b) 27<3ⁿ<243 => 3³<3ⁿ<3⁵ => n=4

Bài 2: Thực hiện phép tính  ( 4 điểm)

\((\frac{1}{{4.9}} + \frac{1}{{9.14}} + \frac{1}{{14.19}} + ... + \frac{1}{{44.49}})\frac{{1 - 3 - 5 - ... - 49}}{{89}}\)

\( = \frac{1}{5}(\frac{1}{4} - \frac{1}{9} + \frac{1}{9} - \frac{1}{{14}} + \frac{1}{{14}} - \frac{1}{{19}} + ... + \frac{1}{{44}} - \frac{1}{{49}}).\frac{{2 - (1 + 3 + 5 + 7 + ... + 49)}}{{12}}\)

\( = \frac{1}{5}.(\frac{1}{4} - \frac{1}{{49}}).\frac{{2 - (12.50 + 25)}}{{89}} =  - \frac{{5.9.7.89}}{{5.4.7.7.89}} =  - \frac{9}{{28}}\)

Bài 3. ( 4 điểm mỗi câu 2 điểm)

a) Tìm x biết: |2x+3|=x+2

Ta có: \(x + 2 \ge 0\)=>\(x \ge  - 2\)

+ Nếu \(x \ge  - \frac{3}{2}\) thì |2x+3| =x+2

=> 2x+3=x+2 => x= -1 (Thỏa mãn)

+ Nếu \( - 2 \le x <  - \frac{3}{2}\) Thì |2x+3| = x+2

 =>  - 2x – 3 =x+2 => \(x =  - \frac{5}{3}\)( Thỏa mãn)

+ Nếu – 2 >x  Không có giá trị nào của x thỏa mãn

b) Tìm giá trị nhỏ nhất A= |x – 2006| + |2007 – x| Khi x thay đổi

+ Nếu x< 2006 thì A = -x +2006 + 2007 – x = -2x +4013

Khi đó – x> -2006 => -2x +4013 > - 4012 +4013 = 1 => A>1

+ Nếu \(2006 \le x \le 2007\)thì A =x – 2006 +2007 – x =1

+ Nếu x>2007 thì A= x – 2006 – 2007 +x = 2x – 4013

Do x >2007 => 2x – 4013>4014 – 4013 =1 => A>1.

Vậy A đạt giá trị nhỏ nhất là 1 khi \(2006 \le x \le 2007\)

Bài 4. Hiện nay hai kim đồng hồ chỉ 10 giờ. Sau ít nhất bao lâu thì 2 kim đồng hồ nằm đối diện nhau trên một đường thẳng. (4 điểm mỗi)
Gọi x, y là số vòng quay của kim phút và kim giờ khi 10giờ đến lúc 2 kim đối nhau
trên một đường thẳng, ta có:

\(x - y = \frac{1}{3}\)( ứng với từ số 12 đến số 4 trên đồng hồ)

và x:y = 12 (Do kim phút quay nhanh gấp 12 lần kim giờ)
Do đó:\(\frac{x}{y} = \frac{{12}}{1} =  > \frac{x}{{12}} = \frac{y}{1} = \frac{{x - y}}{{11}} = \frac{1}{3}:11 = \frac{1}{{33}}\)

=>\(x = \frac{{12}}{{33}}\)( vòng) => \(x = \frac{4}{{11}}\)( giờ)

Vậy thời gian ít nhất để 2 kim đồng hồ từ khi 10 giờ đến lúc nằm đối diện nhau trên một đường thẳng là \[\frac{4}{{11}}\]giờ

Bài 5. Cho tam giác vuông ABC ( A = 1v), đường cao AH, trung tuyến AM. Trên tia đối tia MA lấy điểm D sao cho DM = MA. Trên tia đối tia CD lấy điểm I sao cho CI = CA, qua I vẽ đường thẳng song song với AC cắt đường thẳng AH tại E. Chứng minh: AE =BC (4 điểm mỗi)

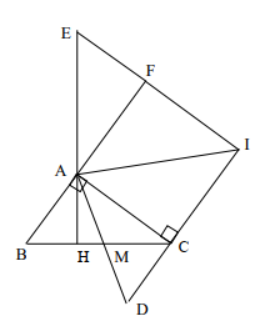
Đường thẳng AB cắt EI tại F

\(\Delta ABM = \Delta DCM\)vì:

AM+DM(gt), MB=MC(gt),

\(\widehat {AMB} = \widehat {DMC}\)(đđ) => \(\widehat {BAM} = \widehat {CDM}\)

=> FB // ID => \(ID \bot AC\)

Và \(\widehat {FAI} = \widehat {CIA}\)( so le trong) (1)

IE // AC (gt) => \(\widehat {FIA} = \widehat {CAI}\)( so le trong) (2)

Từ (1) và (2) => \(\Delta CAI = \Delta FIA\)(AI chung)

=> IC=AC=AF (3)

Và \(\widehat {EFA} = 1v\)(4)

Mặt khác \(\widehat {EAF} = \widehat {BAH}\)(đđ),

\(\widehat {BAH} = \widehat {ACB}\) ( cùng phụ \(\widehat {ABC}\))

=> \(\widehat {EAF} = \widehat {ACB}\)(5)

Từ (3), (4) và (5) => \[\Delta AFE = \Delta CAB\]

=> AE=BC

Đáp án đề 2 toán 7

Bài 1: ( 4 điểm)

Bài 2: (4 điểm)

                                                               \[\]