Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Đề cương ôn tập học kỳ 2 trường THPT Yên Hòa - Hà Nội năm 2019 - 2020, tài liệu bao gồm 19 trang. Tài liệu được tổng hợp từ các tài liệu ôn thi hay nhất giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây
Đề cương ôn tập học kỳ 2 trường THPT Yên Hòa - Hà Nội năm 2019 - 2020
Đề cương ôn tập học kỳ II
A. Kiến thức:
I. Đại số
1. Bất đẳng thức Côsi, bất đẳng thức Bunhiacốpxki. GTLN và GTNN của hàm số.
2. Dấu của nhị thức bậc nhất, tam thức bậc hai.
3. Bất phương trình và hệ bất phương trình bậc nhất, bậc hai một ẩn.
4. Bất phương trình tích, thương.
5. Phương trình, bất phương trình chứa dấu giá trị tuyệt đối, căn thức.
II. Lượng giác
1. Giá trị lượng giác.
2. Cung liên kết.
3. Công thức cộng, nhân đôi, hạ bậc, biến đổi tổng thành tích, tích thành tổng.
III. Hình học
1. Phương trình tổng quát, tham số, chính tắc của đường thẳng.
2. Khoảng cách từ một điểm tới một đường thẳng.
3. Góc giữa hai đường thẳng.
4. Phương trình đường tròn.
5. Elip.
6. Hyperbol.
B. Bài tập tự luyện
Trắc nghiệm
I. Bất đẳng thức và bất phương trình
Câu 1.Với x, y là hai số thực thì mệnh đề nào sau đây là đúng?
A. \(xy < 1 \Rightarrow \left\{ {\begin{array}{*{20}{l}}{x < 1}\\{y < 1}\end{array}.\quad } \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}}{x < 1}\\{y < 1}\end{array} \Rightarrow xy < 1} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{x < 1}\\{y < 1}\end{array} \Rightarrow x + y < 2.} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}}{x < 1}\\{y < 1}\end{array} \Rightarrow x - y < 0} \right.\)
Câu 2.Mệnh đề nào sau đây là đúng?
A. \(a < b \Leftrightarrow ac < bc\).
B \(a < b \Leftrightarrow a + c < b + c\)
C. \(\left\{ {\begin{array}{*{20}{l}}{a < b}\\{c < d}\end{array} \Rightarrow ac < bd.} \right.\)
\[{\rm{\;D}}{\rm{.\;}}a < b \Leftrightarrow \frac{1}{a} > \frac{1}{b}\]
Câu 3.Mệnh đề nào sau đây là đúng?
A. \(\left\{ {\begin{array}{*{20}{l}}{a > b}\\{c > d}\end{array} \Rightarrow ac > bd.} \right.\)
B. \(\left\{ {\begin{array}{*{20}{l}}{a > b}\\{c > d}\end{array} \Rightarrow \frac{a}{c} > \frac{b}{d}} \right.\).
C. \(\left\{ {\begin{array}{*{20}{l}}{a > b}\\{c > d}\end{array} \Rightarrow a - c > b - d.} \right.\)
D. \(\left\{ {\begin{array}{*{20}{l}}{a > b > 0}\\{c > d > 0}\end{array} \Rightarrow ac > bd} \right.\)
Câu 4. Cho \(a,b > 0\) và \(ab > a + b\). Mệnh đề nào sau đây là đúng?
A. \(a + b = 4\).
B. \(a + b > 4\).
C. \(a + b < 4\).
D. \(a + b \le 4\).
Câu 5. Với mọi số a, b dương, bất đẳng thức nào sau đây là sai ?
A. \(a + b \ge 2\sqrt {ab} \).
B. \(\sqrt {ab} \ge \frac{{a + b}}{2}\).
C. \(a + \frac{1}{a} \ge 2\).
D. \({a^2} + {b^2} \ge 2ab\).
Câu 6. Giá trị nhỏ nhất của hàm số \(f(x) = \frac{x}{2} + \frac{2}{{x - 1}}\) với \(x > 1\) là
A. 2 .
B. \(\frac{5}{2}\).
C. \(2\sqrt 2 \).
D. 3 .
Câu 7. Với \(x \ge 2\) thì giá trị lớn nhất của hàm số \(f(x) = \frac{{\sqrt {x - 2} }}{x}\) là
A. \(\frac{1}{{2\sqrt 2 }}\).
B. \(\frac{2}{{\sqrt 2 }}\).
C. \(\frac{{\sqrt 2 }}{2}\).
D. \(\frac{3}{{\sqrt 2 }}\).
Câu 8. Bất phương trình nào sau đây không tương đương với bất phương trình \(x + 5 \ge 0\) ?
A. \({(x - 1)^2}(x + 5) \ge 0\).
B. \( - {x^2}(x + 5) \le 0\).
C. \(\sqrt {x + 5} (x + 5) \ge 0\).
D. \(\sqrt {x + 5} (x - 5) \ge 0\).
Câu 9. Tập nghiệm của bất phương trình \(x + \sqrt {x - 3} \le 3 + \sqrt {x - 3} \) là
A. \(\emptyset \).
B. \(( - \infty ;3)\).
C. \(\{ 3\} \).
D. \([3; + \infty )\).
Câu 10. Bất phương trình \(5x - 1 > \frac{{2x}}{5} + 3\) có nghiệm là
A. \(\forall x \in \mathbb{R}\).
B. \(x < 2\).
C. \(x > - \frac{5}{2}\).
D. \(x > \frac{{20}}{{23}}\).
Câu 11. Tập hợp tất cả các giá trị của m để bất phương trình \(\left( {{m^2} + 2m} \right)x \le {m^2}\) thỏa mãn với mọi x là
A. \(( - 2;0)\).
B. \(\{ - 2;0\} \).
C. \(\{ 0\} \).
D. \([ - 2;0]\).
Câu 12. Tập xác định của hàm số \(y = \sqrt {3 - 2x} + \sqrt {5 - 6x} \) là
A. \(\left( { - \infty ;\frac{5}{6}} \right]\).
B. \(\left( { - \infty ;\frac{6}{5}} \right]\).
C. \(\left( { - \infty ;\frac{3}{2}} \right]\).
D. \(\left( { - \infty ;\frac{2}{3}} \right]\).
Câu 13.Tập xác định của hàm số \(y = \sqrt {x - m} - \sqrt {6 - 2x} \) là một đoạn trên trục số khi và chỉ khi
A. \(m = 3\).
B. \(m < 3\).
C. \(m > 3\).
D. \(m < \frac{1}{3}\).
Câu 14. Tập tất cả các giá trị thực của tham số m để hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3(x - 6) \le - 3}\\{\frac{{5x + m}}{2} \ge 7}\end{array}} \right.\) có nghiệm là
A. \(m > - 11\).
B. \(m \ge - 11\).
C. \(m < - 11\).
D. \(m \le - 11\).
Câu 15. Tập tất cả các giá trị thực của tham số m để hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{x - 3 \le 0}\\{m - x \le 1}\end{array}} \right.\) vô nghiệm là
A. \(m < 4\).
B. \(m > 4\).
C. \(m \le 4\).
D. \(m \ge 4\).
Câu 16. Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{3x + \frac{3}{5} < x + 2}\\{\frac{{6x - 3}}{2} < 2x + 1}\end{array}} \right.\) có nghiệm là
A. \(x < \frac{5}{2}\).
B. \(\frac{7}{{10}} < x < \frac{5}{2}\).
C. \(x < \frac{7}{{10}}\).
D. vô nghiệm.
Câu 17. Cho bất phương trình \(mx + 6 < 2x + 3m\) có tập nghiệm là S. Hỏi tập hợp nào sau đây là phần bù của S với \(m < 2\) ?
A. \((3; + \infty )\).
B. \([3; + \infty )\).
C. \(( - \infty ;3)\).
D. \(( - \infty ;3]\).
Câu 18. Bất phương trình \((m - 1)x + 1 > 0\) có tập nghiệm là \(S = \left( { - \infty ; - \frac{1}{{m - 1}}} \right)\) khi
A. \(m > 1\).
B. \(m \ge 1\).
C. \(m \le 1\).
D. \(m < 1\).
Câu 19. Bất phương trình \(\frac{{x - 1}}{{{x^2} + 4x + 3}} \le 0\) có tập nghiệm là
A. \(( - \infty ;1)\).
B. \(( - 3; - 1) \cup [1; + \infty )\).
C. \(( - \infty ; - 3) \cup ( - 1;1]\).
D. \(( - 3;1)\).
Câu 20. Tập nghiệm của bất phương trình \(\frac{{{x^2} - 5x + 6}}{{x - 1}} \ge 0\) là
A. \((1;3]\).
B. \((1;2] \cup [3; + \infty )\).
C. [2 ; 3]
D. \(( - \infty ;1) \cup [2;3]\).
Câu 21. Dấu của tam thức bậc hai \(f(x) = - {x^2} + 5x - 6\) là
A. \(f(x) < 0\) với \(2 < x < 3\) và \(f(x) > 0\) với \(x < 2\) hoặc \(x > 3\).
B. \(f(x) < 0\) với \( - 3 < x < - 2\) và \(f(x) > 0\) với \(x < - 3\) hoặc \(x > - 2\).
C. \(f(x) > 0\) với \(2 < x < 3\) và \(f(x) < 0\) với \(x < 2\) hoặc \(x > 3\).
D. \(f(x) > 0\) với \( - 3 < x < - 2\) và \(f(x) < 0\) với \(x < - 3\) hoặc \(x > - 2\).
Câu 22. Khi xét dấu biểu thức \(f(x) = \frac{{{x^2} + 4x - 21}}{{{x^2} - 1}}\) ta được
A. \(f(x) > 0\) khi \( - 7 < x < - 1\) hoặc \(1 < x < 3\).
B. \(f(x) > 0\) khi \(x < - 7\) hoặc \( - 1 < x < 1\) hoặc \(x > 3\).
C. \(f(x) > 0\) khi \( - 1 < x < 0\) hoặc \(x > 1\).
D. \(f(x) > 0\) khi \(x > - 1\).
Câu 23. Tập xác định của hàm số \(y = \sqrt {5{x^2} - 4x - 1} \) là
A. \(\left( { - \infty ;\frac{1}{5}} \right] \cup [1; + \infty )\).
B. \(\left[ { - \frac{1}{5};1} \right]\).
C. \(\left( { - \infty ;\frac{{ - 1}}{5}} \right) \cup (1; + \infty )\).
D. \(\left( { - \infty ;\frac{{ - 1}}{5}} \right] \cup [1; + \infty )\).
Câu 24. Tập xác định của hàm số \(y = \sqrt {\frac{2}{{{x^2} + 5x - 6}}} \) là
A. \(( - \infty ; - 6] \cup [1; + \infty )\).
B. \(( - 6;1)\).
C. \(( - \infty ; - 6) \cup (1; + \infty )\).
D. \(( - \infty ; - 1) \cup (6; + \infty )\).
Câu 25.Phương trình \({x^2} - 2(m + 2)x + {m^2} - m - 6 = 0\) có hai nghiệm trái dấu khi và chỉ khi
A. \(m < - 2\).
B. \( - 3 < m < 2\).
C. \(m > - 2\).
D. \( - 2 < m < 3\).
Câu 26. Phương trình \({x^2} - 4mx + m + 3 = 0\) vô nghiệm khi và chỉ khi
A. \(m < 1\).
B. \( - \frac{3}{4} < m < 1\).
C. \(m \le \frac{{ - 3}}{4}\) hoặc \(m \ge 1\).
D. \( - \frac{3}{4} \le m \le 1\).
Câu 27.Giá trị nhỏ nhất \({F_{{\rm{min }}}}\) của biểu thức \(F(x,y) = y - x\) trên miền xác định bởi hệ \(\left\{ {\begin{array}{*{20}{l}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là
A. \({F_{\min }} = 1\).
B. \({F_{{\rm{min }}}} = - 2\).
C. \({F_{\min }} = 3\).
D. \({F_{\min }} = 4\).
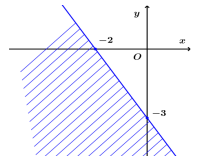
Câu 28.Miền nghiệm của bất phương trình \(3x - 2y > - 6\) là
A.
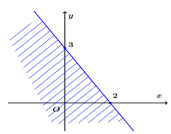
B.
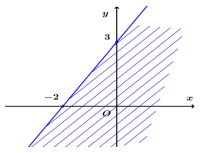
C.
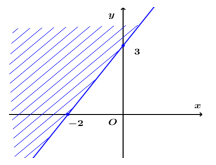
D.
Câu 29. Biểu thức \({\rm{f}}({\rm{x}}) = \left( {{m^2} + 2} \right){x^2} - 2(m - 2)x + 2\) luôn nhận giá trị dương khi và chỉ khi
A. \(m \le - 4\) hoặc \(m \ge 0\).
B. \(m < - 4\) hoặc \(m > 0\).
C. \( - 4 < m < 0\).
D. \(m < 0\) hoặc \(m > 4\).
Câu 30.Tất cả giá trị của m đề \(f(x) = - {x^2} + 2(2m - 3)x - 4m + 3 \le 0,\forall x \in \mathbb{R}\) là
A. \(m > \frac{3}{2}\).
B. \(m > \frac{3}{4}\).
C. \(\frac{3}{4} < m < \frac{3}{2}\).
D. \(1 \le m \le 3\).
Câu 31. Phương trình \({x^2} - (m + 1)x + 1 = 0\) có nghiệm khi và chỉ khi
A. \(m > 1\).
B. \( - 3 < m < 1\).
C. \(m \le - 3\) hoặc \(m \ge 1\).
D. \( - 3 \le m \le 1\).
Câu 32. Với giá trị nào của m thì bất phương trình \({x^2} - x + m \le 0\) vô nghiệm?
A. \(m < 1\).
B. \(m > 1\).
C. \(m < \frac{1}{4}\).
D. \(m > \frac{1}{4}\).
Câu 33.Phương trình \(m{x^2} - mx - 1 = 0\) vô nghiệm khi và chỉ khi
A. \( - 1 < m < 0\).
B. \( - 4 \le m \le 0\).
C. \( - 4 < m \le 0\).
D. \(m < - 4\) hoặc \(m > 0\).
Câu 34. Tất cả giá trị của m để \((m + 1){x^2} + mx + m < 0,\forall x \in \mathbb{R}\) là
A. \(m < - 1\).
B. \(m > - 1\).
C. \(m < - \frac{4}{3}\).
D. \(m > \frac{4}{3}\).
Câu 35. Bất phương trình \(\sqrt { - {x^2} + 6x - 5} > 8 - 2x\) có nghiệm là
A. \(3 < x \le 5\).
B. \(2 < x \le 3\).
C. \( - 5 < x \le - 3\).
D. \( - 3 < x \le - 2\).
Câu 36.Bất phương trình \(\sqrt {2x + 1} < 3 - x\) có tập nghiệm là
A. \(\left[ { - \frac{1}{2};4 - 2\sqrt 2 } \right)\).
B. \((3;4 + 2\sqrt 2 )\).
C. \((4 - 2\sqrt 2 ;3)\).
D. \((4 + 2\sqrt 2 ; + \infty )\).
Câu 37. Nghiệm của bất phương trình \(\left( {{x^2} + x - 2} \right)\sqrt {2{x^2} - 1} < 0\) là
A. \(\left( {1;\frac{{5 - \sqrt {13} }}{2}} \right) \cup (2; + \infty )\).
B. \(\left\{ { - 4; - 5; - \frac{9}{2}} \right\}\).
C. \(\left( { - 2; - \frac{{\sqrt 2 }}{2}} \right) \cup \left( {\frac{{\sqrt 2 }}{2};1} \right)\).
D. \(( - \infty ; - 5] \cup \left[ {5;\frac{{17}}{5}} \right] \cup \{ 3\} \).
Câu 38. Tập nghiệm của bất phương trình \(\frac{{|2 - x|}}{{\sqrt {5 - x} }} > \frac{{x - 2}}{{\sqrt {5 - x} }}\) là
A. \(( - \infty ;2)\).
B. \((2; + \infty )\).
C. \((2;5)\).
D. \(( - \infty ;2]\).
Câu 39. Nghiệm của bất phương trình \(|2x - 3| \le 1\) là
A. \(1 \le x \le 3\).
B. \(1 \le x \le 2\).
C. \( - 1 \le x \le 1\).
D. \( - 1 \le x \le 2\).
Câu 40. Tập nghiệm của bất phương trình \(\frac{{{x^2} + 2x - 8}}{{|x + 1|}} < 0\) là
A. \(( - 4; - 1) \cup ( - 1;2)\).
B. \(( - 4; - 1)\).
C. \(( - 1;2)\).
D. \(( - 2; - 1) \cup ( - 1;1)\).
Câu 41. Tập nghiệm của bất phương trình \(\frac{{\left| {{x^2} - 8x + 12} \right|}}{{\sqrt {5 - x} }} > \frac{{{x^2} - 8x + 12}}{{\sqrt {5 - x} }}\) là
A. ( 2;6)
B. ( 2;5)
C. ( -6; -2)
D. ( 5;6)
Câu 42. Tập nghiệm của hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 7x + 6 < 0}\\{|2x - 1| < 3}\end{array}} \right.\) là
A. (1; 2).
B. [1 ; 2].
C. \(( - \infty ;1) \cup (2; + \infty )\).
D. \(\emptyset \).
Câu 43. Tập xác định của hàm số \(y = \sqrt {4x - 3} + \sqrt {{x^2} + 5x - 6} \) là
A. \([1; + \infty )\).
B. \(\left[ {\frac{3}{4}; + \infty } \right)\).
C. \(\left[ {\frac{3}{4};1} \right]\).
D. \(\left[ { - \frac{6}{5};\frac{3}{4}} \right]\).
Câu 44. Tập nghiệm của bất phương trình \(\sqrt x - 2x \le 0\) là
A. \(\left( {\frac{1}{4}; + \infty } \right)\).
B. \(\left( {0;\frac{1}{4}} \right)\).
C. \(\left[ {0;\frac{1}{4}} \right)\).
D. \(\{ 0\} \cup \left[ {\frac{1}{4}; + \infty } \right)\).
Câu 45. Tập nghiệm của bất phương trình \(|2x + 4| > \sqrt {{x^2} - 6x + 9} \) là
A. \(( - \infty ; - 7) \cup \left( { - \frac{1}{3}; + \infty } \right)\).
B. \(\left( { - 7; - \frac{1}{3}} \right)\).
C. \(\left( { - \infty ;\frac{1}{3}} \right) \cup (7; + \infty )\).
D. \(\left( {\frac{1}{3};7} \right)\).
Câu 46. Tập nghiệm của bất phương trình \(\left| {{x^2} - 5x + 2} \right| - 2 \le 5x\) là
A. \(( - \infty ; - 2] \cup [2; + \infty )\).
B. \([ - 2;2]\).
C. [0 ; 10].
D. \(( - \infty ;0] \cup [10; + \infty )\).
Câu 47.Hệ bất phương trình \(\left\{ {\begin{array}{*{20}{l}}{{x^2} - 1 \le 0}\\{x - m > 0}\end{array}} \right.\) có nghiệm khi
A. \(m > 1\).
B. \(m < 1\).
C. \(m \le 1\).
D. \(m \ne 1\).
Câu 48. Với những giá trị nào của m thì với mọi x ta có \( - 1 \le \frac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7\) ?
A. \(1 < m \le \frac{5}{3}\).
B. \( - \frac{5}{3} \le m < 1\).
C. \(m < 1\).
D. \(m \le - \frac{5}{3}\).
Câu 49. Để bất phương trình \(\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\) nghiệm đúng \(\forall x \in [ - 5;3],a\) phải thỏa mãn
A. \(a \ge 3\).
B. \(a \ge 4\).
C. \(a \ge 5\).
D. \(a \ge 6\).
Câu 50. Trong một cuộc thi pha chế, mỗi đội chơi được sử dụng tối đa 24g hương liệu, 9 lít nước và 210g đường để pha chế nước cam và nước táo.
- Để pha chế một lít nước cam cần 30g đường, 1 lít nước và 1g hương liệu.
- Để pha chế một lít nước táo cần 10g đường, 1 lít nước và 4g hương liệu.
Mỗi lít nước cam nhận được 60 điểm thưởng, mỗi lít nước táo nhận được 80 điểm thưởng. Hỏi cần pha chế bao nhiêu lít nước trái cây mỗi loại để đạt được số điểm thưởng cao nhất?
A. 5 lít nước cam và 4 lít nước táo.
B. 6 lít nước cam và 5 lít nước táo.
C. 4 lít nước cam và 5 lít nước táo.
D. 4 lít nước cam và 6 lít nước táo.
II. Lượng giác
Câu 1. Cung tròn có số đo thì số đo radian của nó là
A. \(180\pi a\).
B. \(\frac{{180\pi }}{a}\).
C. \(\frac{{a\pi }}{{180}}\).
D. \(\frac{\pi }{{180a}}\).
Câu 2. Cung tròn có số đo \(\frac{{5\pi }}{4}\) thì số đo độ của nó là
A. .
B. \.
C. .
D. .
Câu 3. Điểm M biểu diễn góc \(\alpha \) trên đường tròn lượng giác. Biết M nằm trong góc phần tư thứ IV, khẳng định nào sau đây là đúng?
A. \(\sin \alpha > 0\).
B. \(\cos \alpha > 0\).
C. \(\tan \alpha > 0\).
D. \(\cot \alpha > 0\).
Câu 4. Cot \(\alpha \) không xác định khi \(\alpha \) bằng
A. \(\frac{\pi }{4}\).
B. \(\frac{\pi }{3}\).
C. \(\frac{\pi }{2}\).
D. \(\pi \).
Câu 5.Khẳng định nào sau đây là SAI?
A. \(\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}\).
B. \( - 1 \le \sin \alpha \le 1\).
C. \({\sin ^2}\alpha + {\cos ^2}\alpha = 1\).
D. \(\frac{{\cot \alpha }}{{\sin \alpha }} = \frac{{\cos \alpha }}{{{{\sin }^2}\alpha }}(\sin \alpha \ne 0)\).
Câu 6. Khẳng định nào sau đây là sai ?
A. Hai góc lượng giác có cùng tia đầu và có số đo độ là \ và thì có cùng tia cuối.
B. Hai cung lượng giác có củng điểm đầu và có số đo là \(\frac{{3\pi }}{4}\) và \(\frac{{ - 5\pi }}{4}\) thỉ có củng điểm cuối.
C. Hai họ cung lượng giác có củng điểm đầu và có số đo là \(\frac{{3\pi }}{2} + k2\pi (k \in \quad )\) và \( - \frac{{3\pi }}{2} + m2\pi (m \in \quad )\) thì có cùng điểm cuối.
D. Góc có số đo được đổi sang số đo radian là \(\frac{{155\pi }}{9}\).