Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển tập 44 đề thi HSG môn Toán lớp 10, tài liệu bao gồm 44 trang. Đề thi được tổng hợp từ các trường trên cả nước  giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho kỳ thi sắp hới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây

Tuyển tập 44 đề thi HSG môn Toán lớp 10

ĐỀ 1

Câu 1: (2 điểm) Tìm \(m\) để đồ thị hàm số \((P):y = {x^2} - 3x + 2\) cắt đường thẳng \((d):y =  - x + m\) tại hai điểm phân biệt A,B sao cho khoảng cách từ trung điểm I của AB đến hai trục tọa độ bằng nhau.

Câu 2: (5 điểm) Giải phương trình, hệ phương trình:

a) \({x^3} - 3{x^2} + 2\sqrt {{{(x + 2)}^3}}  - 6x = 0\)

b) \(\left\{ {\begin{array}{*{20}{l}}{{x^2} + {x^3}y - x{y^2} + xy - y = 1}\\{{x^4} + {y^2} - xy(2x - 1) = 1}\end{array}} \right.\)

Câu 3: (3 điểm) Cho các số thực dương x, y, z thỏa \(x + y + z = xyz\). Chứng minh

\(\frac{{1 + \sqrt {1 + {x^2}} }}{x} + \frac{{1 + \sqrt {1 + {y^2}} }}{y} + \frac{{1 + \sqrt {1 + {z^2}} }}{z} \le xyz\)

Câu 4: ( 2 điểm) Giải bất phương trình: \[\frac{1}{{\sqrt { - {x^2} + 4x - 3} }} - \frac{1}{{2x - 4}} > 0\]

Câu 5: (4 điểm) Cho hình vuông ABCD, trên cạnh BC lấy điểm E sao cho CE = 2BE. Lấy điểm F trên đường thẳng CD sao cho \(\overrightarrow {CF}  = \frac{1}{2}\overrightarrow {AB} \). Đường thẳng AE và BF cắt nhau tại I.

a) Tính \(\overrightarrow {AI} ;\overrightarrow {CI} \) theo \(\overrightarrow {AB} \) và \(\overrightarrow {AD} \)

b) Chứng minh $AIC={90}^{°}$

Câu 6: (4 điểm) Trong hệ trục Oxy, cho tam giác ABC vuông cân tại A. Đỉnh A(0.2) và M(1, -1) là trung điểm BC. Tìm tọa độ B và C.

ĐỀ 2 .

Câu 1 (2,0 điểm). Cho parabol (P): \[y = {x^2} - 4x - 5\]

a) Khảo sát và vẽ parabol (P).

b) Tìm m để phương trình \({x^2} - 4x - 5 - m = 0\) có đúng một nghiệm thuộc \(( - \infty ;0) \cup (5; + \infty )\).

Câu 2 (4,0 điểm). Giải phương trình và bất phương trình sau:

a) \(\sqrt {3x - 2}  =  - 4{x^2} + 21x - 22\)

b) \(4\sqrt {x + 1}  + 2\sqrt {2x + 3}  \le (x - 1)\left( {{x^2} - 2} \right)\)

Câu 3 (3,0 điểm). Cho hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y + {x^2} + {y^2} = 8}\\{xy(x + 1)(y + 1) = m}\end{array}} \right.\)

a) Giải hệ phương trình khi \(m = 12\).

b) Tìm các giá trị của m để hệ phương trình có nghiệm.

Câu 4 (3,0 điểm).

Cho các số thực dương \({x_1},{x_2},{x_3}, \ldots {x_{2018}}\) thỏa \({x_1} + {x_2} + {x_3} +  \ldots  + {x_{2018}} = 1\).

Tìm giá trị lớn nhất của biểu thức

 \(P = \sqrt {1 - {x_1}}  + \sqrt {1 - {x_2}}  + \sqrt {1 - {x_3}}  +  \ldots  + \sqrt {1 - {x_{2018}}} \).

Câu 5 (4,0 điểm).

Cho tam giác ABC có $AB=c,BC=a,CA=b,BAC={60}^{°}$. Gọi M,N,P là các điểm thỏa mãn: \(2\overrightarrow {MB}  + \overrightarrow {MC}  = \vec 0,3\overrightarrow {NA}  + \overrightarrow {NC}  = \vec 0,\overrightarrow {AP}  = k \cdot \overrightarrow {AB} (k \in \mathbb{R}).\)

a) Tính k theo a, b, c để AM vuông góc PN

b) Gọi I điểm thỏa \(\overrightarrow {IA}  + 7\overrightarrow {IM}  + 8\overrightarrow {IC}  = \vec 0\). Tính tỉ số diện tích của tam giác ABC và tam giác AIC

Câu 6 (4,0 điểm).

Trong mặt phặng tọa độ Oxy cho hình vuông ABCD có tâm \(I(1;1)\). Các điểm \(M( - 2;2),N(2; - 2)\) lần lượt thuộc cạnh AB, CD. Tìm tọa độ các đỉnh của hình vuông ABCD biết đỉnh A có hoành độ dương.

ĐỀ 3

Câu 1(2,0 điểm). Cho parabol \[(P):y = {x^2} + 4x + 3\]

a) Khảo sá và vẽ parabol (P)

b) Tìm m để phương trình \({x^2} + 4x + 4 - m = 0\) không có nghiệm thuộc đoạn \([ - 1,0]\).

Câu 2( 4 điểm). Giải phương trình và bất phương trình sau:

a) \(x + 2\sqrt {x - \frac{1}{x}}  = 3 + \frac{1}{x}\)

b) \({x^2} - 1 \le 2x\sqrt {{x^2} + 2x} \)

Câu 3 (3,0 điểm). Cho hệ phương trình: \(\left\{ {\begin{array}{*{20}{l}}{x + y + \sqrt {xy}  = m}\\{x - y = m}\end{array}} \right.\)

a) Giải hệ phương trình khi m = -3.

b) Tìm các giá trị của m để hệ phương trình có hai nghiệm.

Câu 4 (3,0 điểm). Cho các số thực dương a,b,c thỏa \({a^2} + {b^2} + {c^2} = 1\). Chứng minh rằng:

a) \(\frac{1}{{a\left( {1 - {a^2}} \right)}} \ge \frac{{3\sqrt 3 }}{2}\)

b) \(\frac{a}{{{b^2} + {c^2}}} + \frac{b}{{{a^2} + {c^2}}} + \frac{c}{{{a^2} + {b^2}}} \ge \frac{{3\sqrt 3 }}{2}\)

Câu 5 (4,0 điểm). Cho tam giác ABC đều nội tiếp đường tròn tâm O bán kính R, gọi  lMà điểm bất kì trên đường tròn. Chứng minh rằng:

a) \(M{A^2} + 2\overrightarrow {MB}  \cdot \overrightarrow {MC}  = 3{R^2}\)

b) \(M{A^2} = M{B^2} + M{C^2} - 4\overrightarrow {MB}  \cdot \overrightarrow {MC} \).

Câu 6 (4,0 điểm). Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD, trên đoạn AC lấy điểm M sao cho AC = 4AM và N là trung điểm CD. Chứng minh tam giác BMN vuông cân.

ĐỀ 4 .

Câu 1 ( 4 điểm) Cho hàm số \[y = f(x) = {x^2} - 2(m - 1)x + m\]

1. Tìm m để bất phương trình \(f(x) \ge 0\) có tập nghiệm là \(\mathbb{R}\).

2. Tìm m đề bất phương trình \(f(x) = 0\) có hai nghiệm \({x_1},{x_2}\) lớn hơn 1 .

Câu 2 (4 điểm)

1. Giải phương trình: \(2\sqrt {x - 1}  + 3\sqrt {x - 3}  = \sqrt {{x^2} - 4x + 3}  + 6,(x \in \mathbb{R})\)

2. Giải phương trình: \(\left\{ {\begin{array}{*{20}{l}}{{x^3} + {x^2}y - 2y = 2x{y^2} - 2x}\\{\sqrt {2x - 1}  + \sqrt {2y - 1}  = x + 2y - 1}\end{array}(x,y \in \mathbb{R})} \right.\)

Câu 3 (4 điểm)

1. Giải bât phương trình: \(\sqrt {3x - 2}  + \sqrt {x + 3}  \ge {x^3} + 3x - 1\)

2. Chứng minh biểu thức sau không phụ thuộc vào x :

\(A = {\cos ^4}x - {\sin ^4}x + 2{\sin ^2}x\sqrt[3]{{3\left( {{{\sin }^4}x + {{\cos }^4}x} \right) - 2\left( {{{\sin }^6}x + {{\cos }^6}x} \right)}}\)

Câu 4. ( 6 điểm)

1. Cho tam giác ABC. Chứng minh rằng với G là trọng tâm tam giác ABC ta có

\(\overline {GA}  \cdot \overline {GB}  + \overline {GB}  \cdot \overline {GC}  + \overline {GC}  \cdot \overline {GC}  =  - \frac{1}{6} \cdot \left( {A{B^2} + B{C^2} + C{A^2}} \right)\)

2. Trong mặt phẳng với hệ tọa độ Oxy, cho tam giác ABC vuông tại A(1, 2). Đường thẳng chứa canh BC có phương trình: \({\rm{x}} + {\rm{y}} + 1 = 0\). Tìm tọa độ B và C, biết \({\rm{AB}} = 2{\rm{AC}}\).

3. Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường tròn \(\left( {{{\rm{C}}_1}} \right):{(x - 1)^2} + {(y - 3)^2} = 0\) và \(\left( {{{\rm{C}}_2}} \right):{(x - 2)^2} + {(y + 2)^2} = 5\)

Lập phương trình đường thẳng \(\Delta \) đi qua A(1;0), đồng thời \(\Delta \) cắt các đường tròn \(\left( {{{\rm{C}}_1}} \right)\) và \(\left( {{{\rm{C}}_2}} \right)\) lần lượt tại M,N (M, N không trùng \({\rm{A}}\) )

Câu 5. (2 điểm) Cho các số thực dương a, b, c thỏa mãn \(a + b + c = 3\). Chứng minh rằng

\(\frac{a}{{{a^3} + {b^2} + c}} + \frac{b}{{{b^3} + {c^2} + a}} + \frac{c}{{{c^3} + {a^2} + b}} \le 1\)

ĐỀ 5 .

Câu 1. ( 5,0 điểm)

a) Tìm m để phương trình \(m{x^2} - 2(m - 2)x + 2m - 7 = 0\) ( \(m\) là tham số) có hai nghiệm \({x_1},{x_2}\) thỏa mãn: \(\left| {{x_1} - {x_2}} \right| = \frac{4}{3}\).

b) Tìm tất cả giá trị của tham số m để bất phương trình \(\frac{{{x^2} - 4x - 4}}{{{x^2} - 2(m - 1)x + 16}} \le 2\) thỏa với mọi \(x \in \mathbb{R}\).

Câu 2. ( 5,0 điểm)

a) Cho phương trình \({x^4} - 2(m + 2){x^2} + 2m + 3 = 0\) ( m là tham số). Tìm tất cả giá trị của tham số m để phương trình có 4 nghiệm phân biệt \({x_1},{x_2},{x_3},{x_4}\) thỏa mãn \(x_1^4 + x_2^4 + x_3^4 + x_4^4 = 52\).

b) Giải phương trình \(4{x^2} + 12x\sqrt {x + 1}  = 27(x + 1)\).

Câu 3. ( 5,0 điểm)

a) Cho tam giác A BC có \(BC = a,AC = b,AB = c\), độ dài ba đường cao kẻ từ đỉnh A,B,C lần lượt là \({h_a},{h_b},{h_c}\). Biết rằng \(a\sin A + b\sin B + c\sin C = {h_a} + {h_b} + {h_c}\), chứng minh tam giác ABC đều.

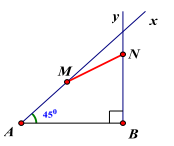
b) Cho hai tia Ax, By với \(AB = 100(\;{\rm{cm}}),xAB = {45^0}\) và \(By \bot AB\). Chất điểm X chuyển động trên tia Ax bắt đầu từ A với vận tốc \(3\sqrt 2 (\;{\rm{cm}}/{\rm{s}})\), cùng lúc đó chất điểm Y chuyển động trên tia By bắt đầu từ B với vận tốc 4 (cm/s). Sau t (giây) chất điểm X di chuyển được đoạn đường AM, chất điểm Y di chuyển được đoạn đường BN. Tìm giá trị nhỏ nhất của M N.

Câu 4. ( 5 điểm)

a) Cho hệ phương trình \[\left\{ {\begin{array}{*{20}{l}}{mx + y = m + 1}\\{x + my = 2}\end{array}} \right.\].Khi hệ có nghiệm duy nhất \(\left( {{x_0};{y_0}} \right)\), hãy tìm giá trị nhỏ nhất của biểu thức \(A = {x_{\rm{o}}}^2 + 2{y_{\rm{o}}} + 5\).

b) Cho tam giác ABC có \(BC = a,CA = b,AB = c\), độ dài ba đường trung tuyến kẻ từ A,B,C lần lượt là \({m_a},{m_b},{m_c}\). Chứng minh rằng: \(\frac{a}{{{m_a}}} + \frac{b}{{{m_b}}} + \frac{c}{{{m_c}}} \ge 2\sqrt 3 \).