Tailieumoi.vn xin giới thiệu bộ đề thi học kì 2 môn Toán lớp 10 sách Kết nối tri thức năm 2024. Tài liệu gồm các đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 2 Toán 10. Mời các bạn cùng đón xem:

Chỉ từ 150k mua trọn bộ Đề thi học kì 2 Toán 10 Kết nối tri thức bản word có lời giải chi tiết (chỉ từ 20k cho 1 đề thi lẻ bất kì):

B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây để thông báo và nhận giáo án.

Xem thử tài liệu tại đây: Link tài liệu

Bộ 20 đề thi học kì 2 Toán lớp 10 Kết nối tri thức có đáp án năm 2024 - Đề 1

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 1)

I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).

Câu 1: Cho hàm số $y=f\left(x\right)$ có tập xác định là $\left[-3;3\right]$ và đồ thị của nó được biểu diễn bởi hình vẽ bên.

 

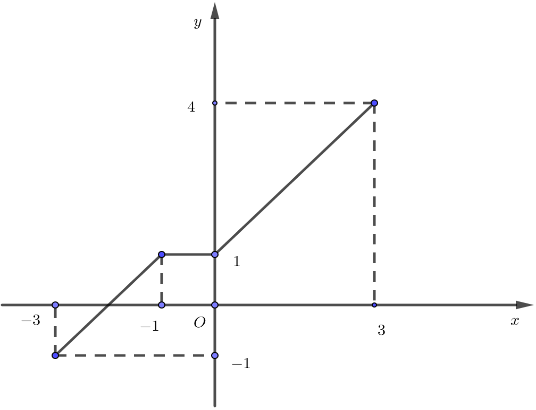
Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên khoảng $\left(-3;3\right)$.                       

B. Hàm số đồng biến trên khoảng $\left(-3;-1\right)$ và $\left(1;3\right)$.

C. Hàm số đồng biến trên khoảng $\left(-3;-1\right)$ và $\left(1;4\right)$.                           

D. Hàm số nghịch biến trên khoảng $\left(-1;0\right)$.

Câu 2: Tập xác định của hàm số $y=\sqrt{2-x}+\frac{x}{\sqrt{7+x}}$ là

A. $\left[2;+\mathrm{\infty }\right)$.                              

B. $\left(-7;2\right]$.

C. $\mathbb{R}\mathrm{\setminus }\left\{-7;2\right\}$. 

D. $\left(-7;2\right)$

Câu 3: Cho hàm số bậc hai $y=a{x}^2+bx+c$ $y=a{x}^2+bx+c$ có đồ thị $y=a{x}^2+bx+c$, đỉnh của $y=a{x}^2+bx+c$ được xác định bởi công thức nào?

A. $y=a{x}^2+bx+c$.  

B. $y=a{x}^2+bx+c$.  

C. $y=a{x}^2+bx+c$.  

D. $y=a{x}^2+bx+c$.

Câu 4: Đồ thị dưới đây là của hàm số nào?

 

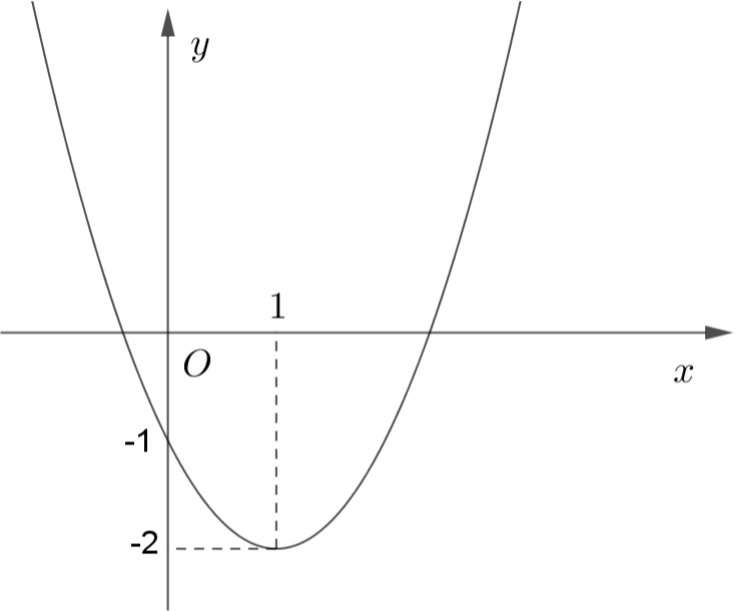
A. $y=x^2+x-4$.   

B. $y=x^2-2x-1$.  

C. $y=-x^2-2x+1$.                                    

D. $y=2x-4$.

Câu 5: Cho tam thức $f(x)=a{x}^2+bx+c(a>0),\mathrm{\Delta }=b^2-4ac$. Mệnh đề nào sau đây đúng?

A. $f(x)\ge 0$với mọi x thuộc $\mathrm{R}$ khi $\mathrm{\Delta }>0$.                 

B. $f(x)<0$với mọi x thuộc $\mathrm{R}$ khi $\mathrm{\Delta }<0$.

C. $f(x)<0$với mọi x thuộc $\mathrm{R}$ khi $\mathrm{\Delta }=0$.                    

D. $f(x)>0$với mọi x thuộc $\mathrm{R}$ khi $\mathrm{\Delta }<0$.

Câu 6:  Tập nghiệm của bất phương trình $-x^2+3x\le 0$ là

A. $\left(-\mathrm{\infty };0\right)\cup \left(3;+\mathrm{\infty }\right)$.              

B. $\left(-\mathrm{\infty };0\right]\cup \left[3;+\mathrm{\infty }\right)$.              

C. $\left(0;3\right)$.                                    

D. $\left[0;3\right]$.

Câu 7: Giá trị $x=2$là nghiệm của phương trình nào sau đây?

A. $\sqrt{x^2-x-4}=\sqrt{x-4}$.

B. $x-2=\sqrt{x-3}$.

C. $x+2=2\sqrt{3x-2}$.                                  

D. $x+2=\sqrt{x+1}$.

Câu 8: Tập nghiệm $S$ của phương trình $\sqrt{2x-3}=x-3$ là:

A. $S=\left\{6\right\}.$

B. $S=\mathrm{\varnothing }.$    

C. $S=\left\{6;2\right\}.$                                       

D. $S=\left\{2\right\}.$

Câu 9:  Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho đường thẳng $d:2x-3y+1=0$. Vectơ nào dưới đây là vectơ pháp tuyến của đường thẳng $d$?

A. $\overrightarrow{n_2}=(2;3)$.                    

B. $\overrightarrow{n_3}=(3;2)$.                             

C. $\overrightarrow{n_1}=(2;-3)$.               

D. $\overrightarrow{n_4}=(-3;2)$.

Câu 10: Phuong trình tổng quát đường thẳng đi qua A(1; 3) có vectơ pháp tuyến  có dạng:

A. $2x-3y+3=0$         

B. $3x-2y+1=0$

C. $3x-2y+3=0$         

D. $2x+3y-1=0$

Câu 11: Cho 2 điểm $A\left(1;-4\right)$,$B\left(1;2\right)$. Viết phương trình tổng quát đường trung trực của đoạn thẳng $AB$.

A. $y-1=0$.   

B. $x-4y=0$.

C. $x-1=0$. 

D. $y+1=0$.

Câu 12:      Khoảng cách từ $I(1;-2)$ đến đường thẳng $\mathrm{\Delta }:3x-4y-26=0$ bằng

A. 3.       

B. $12$.     

C. 5.       

D. $\frac{5}{3}$.

Câu 13:      Cho  $\mathrm{\Delta }:x-3y+1=0$và .$d:3x-y-1=0$ Vị trí của  và d là:

A. Song song với nhau. 

B. Trùng nhau

C. Vuông góc với nhau. 

D. Cắt nhau nhưng không vuông góc với nhau.

Câu 14:      Góc giữa hai đường thẳng $a:\sqrt{3}x-y+7=0$ và $b:x-\sqrt{3}y-1=0$là:

A. ${30}^{\circ }$.                

B. ${90}^{\circ }$.                

C. ${60}^{\circ }$.                

D. ${45}^{\circ }$.

Câu 15: Trong mặt phẳng tọa độ $Oxy$, phương trình nào sau đây là phương trình của đường tròn?

A. $x^2+2y^2-x+8y+1=0$.                       

B. $x^2+y^2+4x+6y-12=0$.

C. $x^2+y^2-2x-8y+25=0$.                      

D. $4x^2-4y^2+9x-6y-1=0$.

Câu 16:      Xác định tâm và bán kính của đường tròn $\left(C\right):{\left(x+1\right)}^2+{\left(y-2\right)}^2=9.$

A. Tâm $I\left(-1;2\right),$ bán kính $R=3$. 

B. Tâm $I\left(-1;2\right),$ bán kính $R=9$.

C. Tâm $I\left(1;-2\right),$ bán kính $R=3$. 

D. Tâm $I\left(1;-2\right),$ bán kính $R=9$.

Câu 17:      Cho phương trình $x^2+y^2-2mx-4\left(m-2\right)y+6-m=0(1)$. Điều kiện của $m$để $(1)$là phương trình của đường tròn.

A. $m=2$.                    

B. $[\begin{array}{l}m<1\\ m>2\end{array}$.                          

C. $1<m<2$.               

D. $[\begin{array}{l}m=1\\ m=2\end{array}$.

Câu 18:      Trong mặt phẳng với hệ trục tọa độ $Oxy$, cho đường tròn$(C)$ có tâm $I(1;-2)$ và bán kính $R=3$. Viết phương trình của đường tròn (C).

A. $(x+1{)}^2+(y-2{)}^2=9$.                           

B. $(x-1{)}^2+(y+2{)}^2=3$.

C. $(x-1{)}^2-(y+2{)}^2=9$.                            

D. $(x-1{)}^2+(y+2{)}^2=9$.

Câu 19:      Parbol $5y^2=12x$có tiêu điểm là:

A. $\left(\frac{3}{5};0\right)$.                           

B. $\left(\frac{6}{5};0\right)$.                                           

C. $\left(\frac{12}{5};0\right)$.                    

D. $\left(\frac{3}{10};0\right)$.

Câu 20:    Phương trình chính tắc của e líp có độ dài trục lớn bằng , trục nhỏ bằng  là:

A. $\frac{x^2}{64}+\frac{y^2}{36}=1$.        

B. $\frac{x^2}{16}-\frac{y^2}{9}=1$.                        

C. $\frac{x^2}{9}+\frac{y^2}{16}=1$.                       

D. $\frac{x^2}{16}+\frac{y^2}{9}=1$.

Câu 21:      Bình có 4 cây bút chì khác nhau và 5 cây bút mực khác nhau. Bình cần chọn một cây bút để tặng bạn, hỏi Bình có bao nhiêu cách chọn?

A. $5.$           B. $4.$ 

C. $9.$            D. $20.$

Câu 22:      Một người vào cửa hàng ăn, người đó chọn thực đơn gồm $1$ món ăn trong $5$ món, $1$ loại quả tráng miệng trong $5$ loại quả tráng miệng và một nước uống trong $3$ loại nước uống. Có bao nhiêu cách chọn thực đơn.

A. $25$.             B. $75$.   

C. $100$.           D. $15$.

Câu 23:      Từ các số $1,2,3$ có thể lập được bao nhiêu số tự nhiên khác nhau và mỗi số có các chữ số khác nhau:

A. $36$              B. $20$. 

C. $72$.              D. $15$.

Câu 24:      Cho hai số tự nhiên $k,n$ thỏa $1\le k\le n$. Mệnh đề nào sau đây đúng?

A. $A_n^k=\frac{n!}{k!(n-k)!}.$                     

B. $A_n^k=\frac{k!(n-k)!}{n!}.$                     

C. $A_n^k=\frac{n!}{\left(n-k\right)!}.$     

D. $A_n^k=\frac{(n-k)!}{n!}.$

Câu 25:      Có bao nhiêu cách xếp 6 bạn thành một hàng dọc?

A. $6^6$.                      B. $5!$. 

C. $6$.                         D. $6!$.

Câu 26:      Tổ 1 của lớp 10A có 10 học sinh gồm 6 nam và 4 nữ. Cô giáo chủ nhiệm chọn 7 em đi lao động, trong đó có 4 nam và 3 nữ. Hỏi cô giáo chủ nhiệm có tất cả bao nhiêu cách chọn?

A. $19.$                          B. $120.$

C. $8640.$                    D. $60.$

Câu 27:      Có 5 quyển sách khác nhau gồm 3 quyển sách Văn và 2 quyển sách Toán. Hỏi có bao nhiêu cách xếp 5 quyển sách trên lên kệ sách dài (xếp hàng ngang) sao cho tất cả quyển sách cùng môn phải đứng cạnh nhau?

A. 12 cách.                      B. 24 cách. 

C. 120 cách.                  D. 16 cách.

Câu 28:      Cho hai đường thẳng song song $a$ và $b$. Trên đường thẳng $a$ có 5 điểm phân biệt, trên đường thẳng $b$ có 7 điểm phân biệt. Tính số tam giác có 3 đỉnh lấy từ các điểm trên hai đường thẳng $a$ và $b$.

A. 175 tam giác.             B. 220 tam giác.

C. 45 tam giác.             D. 350 tam giác.

Câu 29:      Khai triển nhị thức ${\left(2x+y\right)}^5$. Ta được kết quả là

A. $32x^5+16x^{4}y+8x^3{y}^2+4x^2{y}^3+2x{y}^4+y^5$.

B. $32x^5+80x^{4}y+80x^3{y}^2+40x^2{y}^3+10x{y}^4+y^5$.

C. $2x^5+10x^{4}y+20x^3{y}^2+20x^2{y}^3+10x{y}^4+y^5$.

D. $32x^5+10000x^{4}y+80000x^3{y}^2+400x^2{y}^3+10x{y}^4+y^5$.

Câu 30:      Gieo 3 đồng tiền là một phép thử ngẫu nhiên có không gian mẫu là:

A. {NN, NS, SN, SS}

B. .{NNN, SSS, NNS, SSN, NSN, SNS}

C. .{NNN, SSS, NNS, SSN, NSN, SNS, NSS,SNN}

D. .{NNN, SSS, NNS, SSN, NSS, SNN}

Câu 31:      Cho A là một biến cố liên quan phép thử T. Mệnh đề nào sau đây là mệnh đề đúng?

A.  là số lớn hơn 0.                                     

B. $0\le P(A)\le 1$.

C. .$P(A)=0\iff A=\mathrm{\Omega }$           

D.  là số nhỏ hơn 1.

Câu 32:      Gieo một đồng tiền liên tiếp  lần. Số phần tử của không gian mẫu là?

A. 1.     

B. 2.     

C. 4.      

D. 8.

Câu 33:      Gieo một con súc sắc. Xác suất để mặt chấm chẵn xuất hiện là:

A. 0,2              B. 0,3.   

C. 0,4              D. 0,5.

Câu 34:      Một hộp đựng  bi xanh và  bi đỏ, lần lượt rút  viên bi. Xác suất để rút được một bi xanh và 1 bi đỏ là:

A. $\frac{2}{15}$          

B.$\frac{6}{25}$           

C. $\frac{8}{25}$.         

D. $\frac{4}{15}$.

Câu 35:      Có hai hộp bi, hộp thứ nhất có 4 bi đỏ và 3 bi trắng, hộp thứ hai có 2 bi đỏ và 4 bi trắng. Chọn ngẫu nhiên mỗi hộp ra 1 viên bi. Tính xác suất $P$ để chọn được hai viên bi cùng màu.

A. $P=\frac{8}{21}$.   

B. $P=\frac{3}{7}$.        

C. $P=\frac{10}{21}$.

D. $P=\frac{4}{9}$.

II. TỰ LUẬN (04 câu – 3,0 điểm)

Câu 1:      Tìm $m$ để bất phương trình $x^2-2\left(m+1\right)x+2m^2-5m+11<0$ vô nghiệm.

Câu 2:      Khi du lịch đến thành phố St. Louis (Mỹ), ta sẽ thấy một cái cổng lớn có hình parabol hướng bề lõm xuống dưới, đó là cổng Arch. Giả sử ta lập một hệ toạ độ Oxy sao cho một chân cổng đi qua gốc O như Hình 16 (x và y tính bằng mét), chân kia của cổng ở vị trí có tọa độ ( 163,0) . Biết một điểm M trên cổng có toạ độ là (10,43).

 

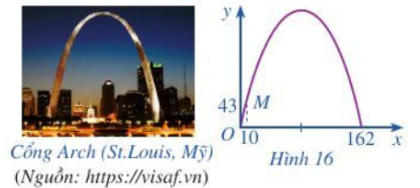
Tính chiều cao của cổng (tính từ điểm cao nhất trên cổng xuống mặt đất), làm tròn kết quả đến hàng đơn vị.

Câu 3:      Trong mặt phẳng với hệ trục tọa độ Oxy, cho hai điểm $A(2;0)$, $B(-2;2)$ và đường thẳng $d:3x+4y+11=0$.

a. Viết phương trình chính tắc của Elip (E), biết (E) có độ dài trục lớn bằng 6 và có một tiêu điểm là A.

b. Gọi (C) là đường tròn đường kính AB; tìm điểm M trên đường thẳng d sao cho qua M vẽ được

hai tiếp tuyến MP, MQ đến (C) (P,Q là hai tiếp điểm) mà đoạn thẳng PQ có độ dài nhỏ nhất.

---------- HẾT ----------

HƯỚNG DẪN GIẢI CHI TIẾT

I. PHẦN TRẮC NGHIỆM (35 câu - 7,0 điểm).

1.B	2.B	3.A	4.B	5.D	6.B	7.C
8.C	9.A	10.C	11.D	12.A	13.D	14.A
15.B	16.A	17.B	18.D	19.A	20.D	21.C
22.B	23.D	24.C	25.D	26.D	27.B	28.B
29.B	30.C	31.B	32.C	33.D	34.D	35.C

 Câu 1:    

Chọn B

Quan sát đồ thị ta thấy hàm số đồng biến trên khoảng $\left(-3;-1\right)$ và $\left(1;3\right)$.

Câu 2:   

Chọn B

Hàm số xác định khi $\{\begin{array}{l}2-x\ge 0\\ 7+x>0\end{array}\iff \{\begin{array}{l}x\le 2\\ x>-7\end{array}$. Vậy tập xác định của hàm số là $\left(-7;2\right]$

Câu 3:

Chọn A

Tọa độ đỉnh của (P):$y=a{x}^2+bx+c$$y=a{x}^2+bx+c$ là $y=a{x}^2+bx+c$

Câu 4: 

Chọn B

Đây là đồ thị của hàm số bậc hai nên loại đáp án D

Bề lõm quay lên tức $a>0$nên loại đáp án C

Đồ thị có trục đối xứng là $x=1$nên ta chọn hàm số $y=x^2-2x-1$

Câu 5:  

Chọn D

$f(x)>0$với mọi x thuộc $\mathrm{R}$ khi $\mathrm{\Delta }<0$.

Câu 6: 

Chọn B

Tam thức $f\left(x\right)=-x^2+3x$ có hai nghiệm $x_1=0;x_2=3$, hệ số $a=-1<0$. Do đó tập nghiệm của bất phương trình $-x^2+3x\le 0$ là $\left(-\mathrm{\infty };0\right]\cup \left[3;+\mathrm{\infty }\right)$.

Câu 7: 

Chọn C

Ta thay $x=2$ vào pt có: $2+2=2\sqrt{3.2-2}\iff 4=4$

Câu 8: 

Chọn A

$\sqrt{2x-3}=x-3\iff \{\begin{array}{l}x\ge 3\\ 2x-3=x^2-6x+9\end{array}\iff \{\begin{array}{l}x\ge 3\\ [\begin{array}{l}x=2\\ x=6\end{array}\end{array}\iff x=6.$

Cách 2: thử đáp án.

Thay $x=2$ vào phương trình ta được $\sqrt{2.2-3}=2-3$ (sai).

Thay $x=6$ vào phương trình ta được $\sqrt{2.6-3}=6-3$ (đúng).

Vậy $x=6$ là nghiệm của phương trình.

Câu 9: 

Chọn C

Câu 10:  

Chọn C

Phương trình đường thẳng đi qua A(1; 3)và có vtpt

$3(x-1)-2(y-3)=0\iff 3x-2y+3=0$

Câu 11:  

Phương pháp

Phương trình tổng quát của đường thẳng đi qua điểm $A\left(x_0,y_0\right)$ và nhận $\overrightarrow{n}=\left(a;b\right)$ làm vecto pháp tuyến là : $d:a(x-x_0)+b(y-y_0)=0$

Lời giải

Chọn D

Ta có $\overrightarrow{AB}=\left(0;6\right)=6\left(0;1\right)$

Gọi là $I$ trung điểm $AB$. Tọa độ điểm $I\left(1;-1\right)$.

Đường trung trực của đoạn thẳng $AB$ đi qua $I$và nhận $\overrightarrow{u_{AB}}=\left(0;1\right)$ là vectơ pháp tuyến nên phương trình đường trung trực của đoạn thẳng $AB$ có dạng: $0\left(x-1\right)+y+1=0\Rightarrow y+1=0$.

Câu 12:  

Phương pháp

Khoảng cách từ điểm $M(x_0;y_0)$ đến đường thẳng $\mathrm{\Delta }:ax+by+c=0$ là: $d(M,\mathrm{\Delta })=\frac{\left|a{x}_0+b{y}_0+c\right|}{\sqrt{a^2+b^2}}$

Lời giải

Chọn A

Vậy khoảng cách từ $I(1;-2)$ đến đường thẳng $\mathrm{\Delta }:3x-4y-26=0$ bằng $d(I,\mathrm{\Delta })=\frac{\left|3.1-4.(-2)-26\right|}{\sqrt{3^2+{(-4)}^2}}=3$

Câu 13:  

Phương pháp

Sử dụng công thức vị trí tương đối của hai đường thẳng.

Lời giải

Chọn D

Ta có  $\frac{1}{3}\ne \frac{-3}{-1}\Rightarrow$d cắt $\mathrm{\Delta }$. Mặt khác ta có 

.$\overrightarrow{n_d}.\overrightarrow{n_{\mathrm{\Delta }}}=1.3+(-3).(-1)=6\ne 0$ Vậy $\mathrm{\Delta }$ cắt d và không vuông góc với nhau.

Câu 14: 

Phương pháp

Áp dụng công thức tính góc giữa hai đường thẳng có:  $\cos \left(a,b\right)=\frac{\overrightarrow{n_1}.\overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}$.

Lời giải

Chọn A

Đường thẳng $a$ có vectơ pháp tuyến là: $\overrightarrow{n_1}=\left(\sqrt{3};-1\right)$;

Đường thẳng $b$ có vectơ pháp tuyến là: $\overrightarrow{n_2}=\left(1;-\sqrt{3}\right)$.

Áp dụng công thức tính góc giữa hai đường thẳng có:

$\cos \left(a,b\right)=\frac{\overrightarrow{n_1}.\overrightarrow{n_2}}{\left|\overrightarrow{n_1}\right|.\left|\overrightarrow{n_2}\right|}=\frac{1.\sqrt{3}+\left(-1\right)\left(-\sqrt{3}\right)}{2.2}=\frac{\sqrt{3}}{2}$. Suy ra góc giữa hai đường thẳng bằng ${30}^{\circ }$.

Câu 15: 

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : $(x-a{)}^2+(y-b{)}^2=R^2$

Lời giải

Chọn B

Để là phương trình đường tròn thì điều kiện cần là hệ số của $x^2$ và $y^2$ phải bằng nhau nên loại được đáp án A và          D.

Ta có:$x^2+y^2-2x-8y+25=0\iff {\left(x-1\right)}^2+{\left(y-4\right)}^2+8=0$vô lý.

Ta có:$x^2+y^2+4x+6y-12=0\iff {\left(x+2\right)}^2+{\left(y+3\right)}^2=25$ là phương trình đường tròn tâm $I\left(-2;-3\right)$, bán kính $R=5$.

Câu 16:

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : $(x-a{)}^2+(y-b{)}^2=R^2$

Lời giải

Chọn A

Câu 17: 

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : $(x-a{)}^2+(y-b{)}^2=R^2$

Lời giải

Chọn B

$x^2+y^2-2mx-4\left(m-2\right)y+6-m=0(1)$là phương trình của đường tròn khi và chỉ khi${\left(m\right)}^2+{\left[2\left(m-2\right)\right]}^2-\left(6-m\right)>0\iff 5m^2-15m+10>0\iff [\begin{array}{l}m<1\\ m>2\end{array}$.

Câu 18: 

Phương pháp

Phương trình đường tròn (O) có tâm I(a,b) và bán kính R là : $(x-a{)}^2+(y-b{)}^2=R^2$

Lời giải

Chọn D

Câu 19: 

Phương pháp

Phương trình chính tắc của parabol: $y^2=2px,p>0$

Tiêu điểm của parabol là $F\left(\frac{p}{2};0\right)$

Lời giải

Chọn A

Từ phương trình chính tắc của parabol: $y^2=2px,p>0$ ta có $p=\frac{12}{5}$.

Tiêu điểm của parabol là $F\left(\frac{p}{2};0\right)\Rightarrow F\left(\frac{3}{5};0\right)$

Câu 20: 

Phương pháp

Phương trình Elip $\left(E\right):\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

Lời giải

Chọn D

Theo bài ra ta có độ dài trục lớn$2a=8\Rightarrow a=4$

Độ dài trục nhỏ $2b=6\Rightarrow a=3$

Vậy phương trình chính tắc của e líp là $\frac{x^2}{16}+\frac{y^2}{9}=1$

Câu 21:

Phương pháp

Áp dụng quy tắc cộng

Lời giải

Chọn C

Theo quy tắc cộng ta có: $5+4=9$

Câu 22: 

Phương pháp

Áp dụng quy tắc nhân

Lời giải

Chọn B

Theo quy tắc nhân ta có: $\mathrm{5.5.3}=75$ cách chọn thực đơn.

Câu 23: 

Phương pháp

Áp dụng quy tắc đếm

Lời giải

Chọn D

TH1: số có $1$ chữ số thì có $3$ cách.

TH2: số có $2$ chữ số và mỗi số có các chữ số khác nhau thì có$3.2=6$số.

TH3: số có $3$ chữ số và mỗi số có các chữ số khác nhau thì có$\mathrm{3.2.1}=6$số

Vậy có$3+6+6=15$số.

Câu 24: 

Phương pháp

Áp dụng công thức chỉnh hợp : $A_n^k=\frac{n!}{\left(n-k\right)!}.$

Lời giải

Chọn C

Ta có $A_n^k=\frac{n!}{\left(n-k\right)!}.$

Câu 25: 

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn D

Mỗi cách xếp là một hoán vị. Số cách xếp là$6!$

Câu 26:

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn D

Số cách chọn: $C_6^4.C_4^3=60$

Câu 27: 

Phương pháp

Áp dụng công thức hoán vị

Lời giải

Chọn B

Các quyển sách cùng môn ta xếp chung một nhóm

Có 2 cách xếp hai nhóm môn Toán và văn

Có $3!$cách xếp sách Văn

Có$2!$ cách xếp sách Toán

Vậy có$3!.2!.2=24$ cách xếp sao cho tất cả quyển sách cùng môn phải đứng cạnh nhau

Câu 28: 

Phương pháp

Áp dụng công thức tổ hợp

Lời giải

Chọn B

TH1: Chọn một trên đường thẳng $a$và hai điểm trên đường thẳng $b$có$5.C_7^2=105$:Tam giác

TH1: Chọn hai trên đường thẳng $a$và một điểm trên đường thẳng $b$có$7.C_5^2=70$:Tam giác

Vậy có$105+70=175$ tam giác

Câu 29: 

Phương pháp

Sử dụng công thức khai triển nhị thức Newton

Lời giải

Chọn B

${\left(2x+y\right)}^5=C_5^0{\left(2x\right)}^5+C_5^1{\left(2x\right)}^{4}y+C_5^2{\left(2x\right)}^3{y}^2+C_5^3{\left(2x\right)}^2{y}^3+C_5^4\left(2x\right)y^4+C_5^5{y}^5$$=32x^5+80x^{4}y+80x^3{y}^2+40x^2{y}^3+10x{y}^4+y^5$

Câu 30: 

Chọn C

Câu 31:

Phương pháp

Công thức tính xác suất

Lời giải

Chọn B

$0\le P(A)\le 1$

Câu 32: 

Phương pháp

Quy tắc đếm trong xác suất

Lời giải

Chọn C

$n(\mathrm{\Omega })=4$

Câu 33: 

Chọn D

Câu 34:   

Chọn D

Câu 35:

Chọn C

Phép thử: Rút mỗi hộp một viên bi

Ta có $n(\mathrm{\Omega })=7.6=42$

Biến cố : Rút được hai viên bi cùng mẫu

TH1: Hai viên màu đỏ có $4.2=8$cách

TH2: Hai viên màu trắng có$3.4=12$ cách

$n(A)=12+8=20\Rightarrow P(A)=\frac{n(A)}{n(\mathrm{\Omega })}=\frac{20}{42}=\frac{10}{21}$.

II. TỰ LUẬN (04 câu – 3,0 điểm)

Câu 1:

Bất phương trình vô nghiệm khi $x^2-2\left(m+1\right)x+2m^2-5m+11\ge 0\mathrm{\forall }x\in \mathbb{R}$

$\iff \{\begin{array}{l}a=1>0\\ {\mathrm{\Delta }}^{\prime }\le 0\end{array}\iff \{\begin{array}{l}1>0\\ m^2+2m+1-\left(2m^2-5m+11\right)\le 0\end{array}$$\iff -m^2+7m-10\le 0\iff [\begin{array}{l}m\le 2\\ m\ge 5\end{array}$

Vậy $m\in \left(-\mathrm{\infty };2\right]\cup \left[5;+\mathrm{\infty }\right)$.

Câu 2:

Từ đồ thị ta thấy các điểm thuộc đồ thị là:$O(0;0),M(10;43),A(162;0)$

Gọi hàm số là

Thay tọa độ các điểm $O,M,A$ vào ta được hệ:

$\{\begin{array}{l}a{.0}^2+b.0+c=0\\ a{.10}^2+b.10+c=43\\ a{.162}^2+b.162+c=0\end{array}\iff \{\begin{array}{l}c=0\\ 100.a+10b=43\\ a{.162}^2+b.162=0\end{array}\iff \{\begin{array}{l}c=0\\ a=-\frac{43}{1520}\\ b=\frac{3483}{760}\end{array}$

Từ đó ta có $y=-\frac{43}{1520}{x}^2+\frac{3483}{760}x$

Hoành độ đỉnh của đồ thị là: $x=-\frac{b}{2a}=81$

Khi đó: $y=-\frac{43}{1520}{81}^2+\frac{3483}{760}.81\approx 186$(m)

Vậy chiều cao của cổng là 186m.

Câu 3:  

a. phương trình chính tắc của elip (E) có dạng $\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0).$

+ (E) có độ dài trục lớn bằng 6 nên a=3.

+ (E) có một tiêu điểm là $A(2;0)$ nên c=2.

$c=2\iff c^2=4\iff a^2-b^2=4\iff 3^2-b^2=4\iff b^2=5$.

Suy ra phương trình chính tắc của elip (E) là $\frac{x^2}{9}+\frac{y^2}{5}=1$

b.

 

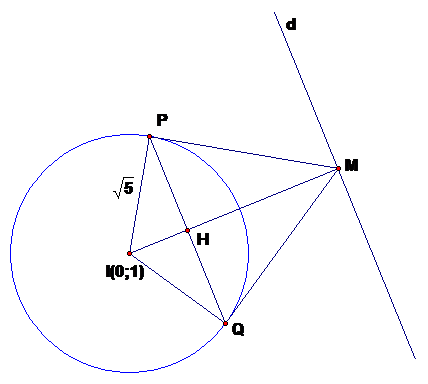
+ Đường tròn (C) có tâm I(0;1), bán kính

$R=\sqrt{5}$.

+ $d\left(I,d\right)=3>R$ nên (C) và d không có điểm chung.

+ Gọi H là trung điểm của PQ. Suy ra PQ có độ dài nhỏ nhất khi PH có độ dài nhỏ nhất.

+ $\frac{1}{P{H}^2}=\frac{1}{5}+\frac{1}{P{M}^2}$. Suy ra PH có độ dài nhỏ nhất khi PM có độ dài nhỏ nhất.

+ $P{M}^2=I{M}^2-5$. Suy ra PM có độ dài nhỏ nhất khi IM có độ dài nhỏ nhất.

+ IM có độ dài nhỏ nhất khi M là hình chiếu vuông góc của I lên d.

+ Xác định được điểm $M\left(-\frac{9}{5};-\frac{7}{5}\right)$.

---------- HẾT ----------       

Bộ 20 đề thi học kì 2 Toán lớp 10 Kết nối tri thức có đáp án năm 2024 - Đề 2

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 2)

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1. Một lớp có 31 học sinh nam và 16 học sinh nữ. Có bao nhiêu cách chọn một học sinh làm lớp trưởng của lớp.

A. 31;         

B. 16;          

C. 47;          

D. 15.

Câu 2. Số cách sắp xếp 6 bạn học sinh thành một hàng dọc là:

A. 6 cách;             

B. 12 cách;            

C. 720 cách;          

D. 18 cách.

Câu 3. Có bao nhiêu số tự nhiên có 5 chữ số, các chữ số khác 0 và đôi một khác nhau.

A. 5!;          

B. 9⁵;          

C. $A_9^5$;                   

D. 5⁹.

Câu 4. Khai triển biểu thức (a + 2b)⁵ ta thu được kết quả là: 

A. a⁵ + 10a⁴b + 40a³b² + 80a²b³ + 80ab⁴ + 32b⁵;               

B. a⁵ – 10a⁴b – 40a³b² – 80a²b³ – 80ab⁴ – 32b⁵;                

C. a⁵ + 20a⁴b + 30a³b² + 80a²b³ + 80ab⁴ + 32b⁵;               

D. a⁵ + 10a⁴b + 40a³b² + 60a²b³ + 60ab⁴ + 32b⁵.

Câu 5. Tổng các hệ số trong khai triển $P\left(x\right)={\left(1+x\right)}^5$ là:

A. 30;         

B. 31;          

C. 32;          

D. 33.

Câu 6. Giá trị nào dưới đây là giá trị chính xác của số π ?

A. 3,14;      

B. 3,1;         

C. 3,146;               

D. Không có câu trả lời đúng.

Câu 7. Quy tròn số 3,1234567 đến hàng phần nghìn. Số gần đúng nhận được là:

A. 3,124;

B. 3,123;

C. 3,12;

D. 3,1235.

Câu 8. Thực hiện đo chiều dài của bốn cây cầu, kết quả đo đạc nào trong các kết quả sau đây là chính xác nhất?

A. 15,34 m ± 0,01 m;

B. 127,4 m ± 0,2 m;

C. 2135,8 m ± 0,5 m;

D. 63,47 m ± 0,15 m.

Câu 9. Giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là

A. trung bình;

B. tứ phân vị;

C. trung vị;

D. mốt.

Câu 10. Cho mẫu số liệu sau: 11; 16; 17; 19; 20; 21; 22; 23; 23; 24; 25. Trung vị của mẫu số liệu là

A. 21;

B. 20,5;

C. 21,5;

D. 22.

Câu 11. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:

So sánh Q₃ và Q₁  ?

A. Q₃ > Q₁;

B. Q₃ < Q₁;  

C. Q₁ = Q₃;

D. Q₃ = 3Q₁.  

Câu 12. Điểm thi học kì I môn Toán của lớp 10A được thống kê trong bảng sau:

Điểm trung bình môn Toán của lớp 10A₂ là

A. 4;

B. 5,5;

C. 5,45;

D. 6.

Câu 13. Chọn khẳng định đúng: “Trong một mẫu số liệu, khoảng biến thiên là…”

A. hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

B. tổng số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

C. tích giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó;

D. thương giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Câu 14. Sản lượng lúa (đơn vị là tạ) của 40 thửa ruộng thí nghiệm có cùng diện tích được trình bày trong bảng số liệu sau:

Phương sai của bảng số liệu trên là:

A. 1,52;

B. 1,53;

C. 1,54;

D. 1,55.

Câu 15. Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:

Khoảng tứ phân vị của bảng số liệu trên là:

A. 30;

B. 10;

C. 20;

D. 5.

Câu 16. Gieo một đồng xu ba lần liên tiếp. Xác suất để ba lần tung kết quả giống nhau là:

A. 0,25;

B. 0,5;

C. 1;

D. 0,75.

Câu 17. Một túi chứa 2 viên bi màu trắng và 3 viên bi màu đen. Lấy ngẫu nhiên 3 viên bi. Xác suất để lấy được ít nhất 1 bi trắng là:

A. 0,9;

B. 0,8;

C. 0,1;

D. 0,2.

Câu 18. Xác suất của biến cố A, kí hiệu là:

A. P(A);

B. n(A);

C. C(A);

D. Ω(A).

Câu 19. Trong mặt phẳng tọa độ Oxy, cho G(3; 5). Tọa độ của $\overrightarrow{OG}$ là

A. (3; –5);             

B. (5; 3);               

C. (–3; –5);           

D. (3; 5).

Câu 20. Trong mặt phẳng tọa độ Oxy, cho hai điểm $M\left(x_M;y_M\right)$ và $N\left(x_N;y_N\right)$. Khi đó ta có tọa độ $\overrightarrow{MN}$ là:

A. $\overrightarrow{MN}=\left(x_N+x_M;y_N+y_M\right)$;            

B. $\overrightarrow{MN}=\left(x_M-x_N;y_N-y_M\right)$;             

C. $\overrightarrow{MN}=\left(x_M-x_N;y_M-y_N\right)$;             

D.$\overrightarrow{MN}=\left(x_N-x_M;y_N-y_M\right)$.

Câu 21. Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của $\overrightarrow{BC}$ là:

A.$\overrightarrow{BC}=\left(6;-1\right)$;             

B.$\overrightarrow{BC}=\left(-6;1\right)$;              

C.$\overrightarrow{BC}=\left(4;5\right)$;               

D. $\overrightarrow{BC}=\left(-6;-1\right)$.

Câu 22. Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{a}=\left(a_1;a_2\right),\overrightarrow{b}=\left(b_1;b_2\right)$ và $\overrightarrow{x}=\left(a_1+b_1;a_2+b_2\right)$. Khi đó $\overrightarrow{x}$ bằng:

A.$\overrightarrow{a}.\overrightarrow{b}$;                  

B.$\overrightarrow{a}+\overrightarrow{b}$;               

C.$\overrightarrow{a}-\overrightarrow{b}$;               

D.$k\overrightarrow{a}\left(k\in ℝ\right)$.

Câu 23. Trong mặt phẳng tọa độ Oxy, cho$\overrightarrow{u}=\left(3;-6\right)$. Khi đó $\frac{1}{2}\overrightarrow{u}$ là:

A. $\frac{1}{2}\overrightarrow{u}=\left(6;-12\right)$;           

B. $\frac{1}{2}\overrightarrow{u}=\left(\frac{5}{2};-\frac{13}{2}\right)$;                   

C. $\frac{1}{2}\overrightarrow{u}=\left(\frac{7}{2};-\frac{11}{2}\right)$;         

D. $\frac{1}{2}\overrightarrow{u}=\left(\frac{3}{2};-3\right)$.

Câu 24. Cho đường thẳng d có phương trình:$\left\{\begin{array}{l}x=2+3t\\ y=-3-t\end{array}\right.$ .  Một vectơ chỉ phương của d có tọa độ là:

A. (2; –3);             

B. (3; –1);             

C. (3; 1);               

D. (3; –3).

Câu 25. Cho đường thẳng ∆: x – 3y – 2 = 0. Tọa độ của vectơ nào sau đây không phải là vectơ pháp tuyến của ∆?

A.${\overrightarrow{n}}_1=\left(1;-3\right)$;                

B.${\overrightarrow{n}}_2=\left(-2;6\right)$;               

C.${\overrightarrow{n}}_3=\left(\frac{1}{3};-1\right)$;              

D.${\overrightarrow{n}}_4=\left(3;1\right)$.

Câu 26. Cho tam giác ABC có tọa độ 3 đỉnh A(4; 5), B(–6; –1), C(1; 1). Phương trình đường cao BH của tam giác ABC là:

A. 3x – 4y – 14 = 0;                  

B. 3x + 4y – 22 = 0;                  

C. 3x + 4y + 22 = 0;                 

D. 3x – 4y + 14 = 0.

Câu 27. Cho tam giác ABC có tọa độ đỉnh B(4; –3). Đường trung tuyến AM có phương trình $\left\{\begin{array}{l}x=1+3t\\ y=-2-7t\end{array}\right.$. Đường cao AH có phương trình 2x + 5y + 66 = 0. Khi đó phương trình đường trung trực của cạnh AB có phương trình là:

A. 13x – 3y + 100 = 0;              

B. 3x – 13y – 140 = 0;              

C. 3x – 13y + 140 = 0;              

D. 13x + 3y – 100 = 0.

Câu 28. Cho đường thẳng d₁, d₂ có vectơ pháp tuyến lần lượt là ${\overrightarrow{n}}_1=\left(a;b\right),{\overrightarrow{n}}_2=\left(c;d\right)$. Kết luận nào sau đây đúng?

A. $\cos \left(d_1,d_2\right)=\frac{\left|ab+cd\right|}{\sqrt{a^2+c^2}.\sqrt{b^2+d^2}}$;             

B. $\cos \left(d_1,d_2\right)=\frac{\left|ac+bd\right|}{\sqrt{a^2+c^2}.\sqrt{b^2+d^2}}$;              

C.$\cos \left(d_1,d_2\right)=\frac{\left|ac+bd\right|}{\sqrt{a^2+b^2}.\sqrt{c^2+d^2}}$;              

D.$\cos \left(d_1,d_2\right)=\frac{ac+bd}{\sqrt{a^2+b^2}.\sqrt{c^2+d^2}}$.

Câu 29. Vị trí tương đối của hai đường thẳng$d_1:\frac{x}{2}-\frac{y}{3}=1$ và d₂: 6x – 4y – 8 = 0 là:

A. Song song;                 

B. Trùng nhau;               

C. Cắt nhau nhưng không vuông góc với nhau;                

D. Vuông góc với nhau.

Câu 30. Tâm của đường tròn (C) có phương trình: (x – 2)² + (y + 5)² = 12 là:

A. D(2; 5);            

B. E(5; 2);             

C. F(2; –5);           

D. G(–2; 5).

Câu 31. Đường tròn tâm I(1; 4) và đi qua điểm B(2; 6) có phương trình là:

A. (x + 1)² + (y + 4)² = 5;         

B.${\left(x-1\right)}^2+{\left(y-4\right)}^2=\sqrt{5}$;                 

C.${\left(x+1\right)}^2+{\left(y+4\right)}^2=\sqrt{5}$;                 

D. (x – 1)² + (y – 4)² = 5.

Câu 32. Cho đường tròn (C): (x – 2)² + (y – 2)² = 9. Phương trình tiếp tuyến của (C) đi qua điểm A(5; –1) là:

A. x + y – 4 = 0 hoặc x – y – 2 = 0;              

B. x = 5 hoặc y = –1;                

C. 2x – y – 3 = 0 hoặc 3x + 2y – 2 = 0;                   

D. 3x – 2y – 2 = 0 hoặc 2x + 3y + 5 = 0.

Câu 33. Cho hai điểm F₁, F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0) và một số a < c và a > 0. Tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a được gọi là:

A. Đường hypebol;                   

B. Đường elip;                

C. Đường parabol;          

D. Đường tròn.

Câu 34. Điểm nào là tiêu điểm của parabol y² = 5x?

A. F(5; 0);             

B. $F\left(\frac{5}{2};0\right)$;          

C.$F\left(\pm \frac{5}{4};0\right)$;                  

D.$F\left(\frac{5}{4};0\right)$.

Câu 35. Cho elip (E): 9x² + 36y² – 144 = 0. Tỉ số$\frac{c}{a}$bằng:

A.$\frac{\sqrt{3}}{2}$;                 

B.$\frac{2\sqrt{3}}{3}$;               

C.$\sqrt{3}$;                  

D.$\frac{\sqrt{3}}{3}$.

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1,0 điểm)

Một bàn dài có hai dãy ghế ngồi đối diện nhau, mỗi dãy gồm 4 ghế. Người ta xếp chỗ ngồi cho 4 học sinh trường A và 4 học sinh trường B vào bàn nói trên. Hỏi xác suất xếp các học sinh vào hai dãy ghế sao cho bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau?

Câu 2. (1,0 điểm)

Sản lượng lúa (tạ) của 40 thửa ruộng thí nghiệm (cho giống lúa mới) có cùng diện tích được trình bày trong bảng phân bố tần số sau đây:

Sản lượng	20	21	22	23	24
Tần số	5	8	11	10	6

Hỏi sản lượng lúa trung bình thu được là bao nhiêu tạ? Tìm khoảng tứ phân vị của dãy số liệu trên.

Câu 3. (1,0 điểm)

Trong mặt phẳng Oxy, cho đường tròn (C): x² + y² – 2x + 2y – 2 = 0.

a) Viết phương trình đường thẳng (∆) song song với (d): 4x – 3y + 3 = 0 và tiếp xúc với (C).

b) Viết phương trình đường thẳng (d) qua A(3; 2) và tiếp xúc với (C).

c) Tìm điểm M thuộc (d’): x – 2y – 1 = 0 sao cho từ M vẽ được hai tiếp tuyến đến (C) vuông góc với nhau.

HƯỚNG ĐẪN ĐÁP ÁN ĐỀ SỐ 01

I. TRẮC NGHIỆM (7 ĐIỂM)

BẢNG ĐÁP ÁN

1. C	2. C	3. C	4. A	5. C	6. D	7. B
8. C	9. D	10. A	11. A	12. C	13. A	14. C
15. B	16. A	17. A	18. A	19. D	20. A	21. A
22. B	23. D	24. B	25. D	26. C	27. B	28. C
29. A	30. C	31. D	32. B	33. A	34. D	35. A

HƯỚNG DẪN CHI TIẾT

Câu 1.

Hướng dẫn giải

Đáp án đúng là: C

Theo quy tắc cộng ta có số cách chọn một học sinh làm lớp trưởng là:

31 + 16 = 47 (cách).

Câu 2.

Hướng dẫn giải

Đáp án đúng là: C

Mỗi cách xếp thứ tự vào hàng của 6 học sinh là một hoán vị của 6 học sinh

Vậy số cách sắp xếp là: 6! = 6 . 5. 4 . 3. 2. 1 = 720 cách xếp.

Câu 3.

Hướng dẫn giải

Đáp án đúng là: C

Vì các chữ số khác 0 nên các chữ số có thể tham gia lập số gồm có 1; 2; 3; 4; 5; 6; 7; 8; 9.

Mỗi cách lập số tự nhiên gồm 5 chữ số khác nhau từ 9 chữ số trên là một chỉnh hợp chập 5 của 9.

Do đó, số các số lập được là $A_9^5$.

Câu 4.

Hướng dẫn giải

Đáp án đúng là: A

Ta có:

(a + 2b)⁵

= $C_5^0{a}^5+C_5^1{a}^{5-1}{\left(2b\right)}^1+C_5^2{a}^{5-2}{\left(2b\right)}^2+C_5^3{a}^{5-3}{\left(2b\right)}^3+C_5^4{a}^{5-4}{\left(2b\right)}^4+C_5^5{\left(2b\right)}^5$

= a⁵ + 10a⁴b + 40a³b² + 80a²b³ + 80ab⁴ + 32b⁵.

Câu 5.

Hướng dẫn giải

Đáp án đúng là: C

Ta có:

${\left(1+x\right)}^5=C_5^0{.1}^5+C_5^1{.1}^4.x+C_5^2{.1}^3.x^2+C_5^3{.1}^2.x^3+C_5^4\mathrm{.1.}{x}^4+C_5^5.x^5$

=$1+5x+10x^2+10x^3+5x^4+x^5$.

Tổng các hệ số là: 1 + 5 + 10 + 10 + 5 + 1 = 32.

Câu 6.

Hướng dẫn giải

Đáp án đúng là: D

Vì​​ π = 3,14592653...​​ là một số thập phân vô hạn không tuần hoàn, nên ta chỉ viết được gần đúng của nó.

Câu 7.

Hướng dẫn giải

Đáp án đúng là: B

Quy tròn số 3,1234567 đến hàng phần nghìn ta nhận được số gần đúng là 3,123 (vì 4 < 5).

Câu 8.

Hướng dẫn giải

Đáp án đúng là: C

Sai số tương đối của kết quả các phép đo lần lượt là:

${\delta }_1=\frac{0,01}{15,34}=0,\mathrm{00065189...}$

${\delta }_2=\frac{0,2}{127,4}=0,\mathrm{00156985...}$

${\delta }_3=\frac{0,5}{2135,8}=0,\mathrm{00023410...}$

${\delta }_4=\frac{0,15}{63,47}=0,\mathrm{00236332...}$

Ta thấy ${\delta }_3$ là nhỏ nhất nên phép đo thứ 3 có kết quả chính xác nhất.

Câu 9.

Hướng dẫn giải

Đáp án đúng là: D

Giá trị xuất hiện nhiều nhất trong mẫu số liệu được gọi là mốt.

Câu 10

Hướng dẫn giải

Đáp án đúng là; A

Mẫu số liệu được sắp xếp theo chiều không giảm và có 11 giá trị là số lẻ nên trung vị là số liệu số 6 và bằng 21.

Câu 11.

Hướng dẫn giải:

Đáp án đúng là: A

Sắp thứ tự mẫu số liệu gồm n = 31 số liệu thành một dãy không giảm ta có:

25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35; 35; 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45; 45.

Tứ phân vị thứ hai Q₂ là: 35

Do n là số lẻ nên Q₁ bằng trung vị của nửa dãy phía dưới (không bao gồm Q₂) tức là trung vị của dãy số liệu: 25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35. Vậy Q₁ = 30. Tương tự, Q₃ là trung vị của nửa dãy phía trên (không bao gồm Q₂) tức là trung vị của dãy số liệu: 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45; 45. Vậy Q₃ = 40.

Vậy, Q₃ > Q₁.

Câu 12.

Hướng dẫn giải

Đáp án đúng là: C

Ta có bảng tần số:

Điểm	1	2	3	4	5	6	7	8	9	10
Tần số	3	3	2	5	9	8	4	3	2	1

Khi đó điểm trung bình của lớp 10A là:

$\overline{x}=\frac{1.3+2.3+3.2+4.5+5.9+6.8+7.4+8.3+9.2+10.2}{40}=5,45$.

Câu 13.

Hướng dẫn giải

Đáp án đúng là: A

Trong một mẫu số liệu, khoảng biến thiên là hiệu số giữa giá trị lớn nhất và giá trị nhỏ nhất của mẫu số liệu đó.

Câu 14.

Hướng dẫn giải

Đáp án đúng là: C

Ta có số trung bình cộng:

$\begin{array}{l}\overline{x}=\frac{20.5+21.8+22.11+23.10+24.6}{40}\\ =22,1\end{array}$

Phương sai:

$s^2=\frac{n_1{\left(x_1-\overline{x}\right)}^2+n_2{\left(x_2-\overline{x}\right)}^2+\mathrm{...}+n_n{\left(x_n-\overline{x}\right)}^2}{n}$

$=\frac{5.{\left(20-22,1\right)}^2+8.{\left(21-22,1\right)}^2+11.{\left(22-22,1\right)}^2+\mathrm{......}+6.{\left(24-22,1\right)}^2}{40}$

$=1,54$

Câu 15.

Hướng dẫn giải:

Đáp án đúng là: B

Sắp thứ tự mẫu số liệu gồm n = 31 số liệu thành một dãy không giảm ta có:

25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35; 35; 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45; 45.

Tứ phân vị thứ hai Q₂ là: 35

Q₁ bằng trung vị của nửa dãy phía dưới (không bao gồm Q₂) tức là trung vị của dãy số liệu: 25; 25; 25; 25; 30; 30; 30; 30; 30; 30; 30; 35; 35; 35; 35. Vậy Q₁ = 30.

Q₃ bằng trung vị của nửa dãy phía trên (không bao gồm Q₂) tức là trung vị của dãy số liệu: 35; 35; 35; 35; 35; 40; 40; 40; 40; 40; 40; 45; 45; 45; 45. Vậy Q₃ = 40.

Khoảng tứ phân vị là: Δ_Q = Q₃ – Q₁ = 40 – 30 = 10.

Câu 16.

Hướng dẫn giải:

Đáp án đúng là: A

Gọi S là kí hiệu khi đồng xu xuất hiện mặt sấp, N là kí hiệu khi đồng xu xuất hiện mặt ngửa.

Không gian mẫu là:

Ω = {SSN; SSS; SNN; SNS; NSS; NSN; NNS; NNN} và n(Ω) = 8.

Gọi biến cố A: “ba lần tung kết quả giống nhau”. Các kết quả thuận lợi của A là: SSS, NNN.

Do đó, n(A) = 2

Vậy xác suất để hai lần tung kết quả khác nhau là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{2}{8}=0,25$.

Câu 17.

Hướng dẫn giải

Đáp án đúng là: A

Túi chứa tổng số viên bi là: 2 + 3 = 5 (viên)

Ta có: n(Ω) = $C_5^3=10$

Xét biến cố A: “lấy được ít nhất 1 bi trắng” và biến cố đối$\overline{A}$: “Chỉ lấy được toàn viên bi đen”.

Ta có: n($\overline{A}$$C_3^3=1$

Do đó,$P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{1}{10}=0,1$

Câu 18.

Hướng dẫn giải:

Đáp án đúng là: A

Xác suất của biến cố A, kí hiệu là: P(A).

Câu 19.

Hướng dẫn giải

Đáp án đúng là: D

Ta có G(3; 5).

Suy ra tọa độ của $\overrightarrow{OG}=\left(3;5\right)$.

Vậy ta chọn phương án D.

Câu 20.

Hướng dẫn giải

Đáp án đúng là: D

Trong mặt phẳng tọa độ Oxy, cho hai điểm $M\left(x_M;y_M\right)$ và $N\left(x_N;y_N\right)$.

Ta có $\overrightarrow{MN}=\left(x_N-x_M;y_N-y_M\right)$.

Vậy ta chọn phương án D.

Câu 21.

Hướng dẫn giải

Đáp án đúng là: A

Ta có:

⦁ Hoành độ của $\overrightarrow{BC}$ là: x_C – x_B = 5 – (–1) = 6;

⦁ Tung độ của $\overrightarrow{BC}$ là: y_C – y_B = 2 – 3 = –1.

Suy ra $\overrightarrow{BC}=\left(6;-1\right)$.

Vậy ta chọn phương án A.

Câu 22.

Hướng dẫn giải

Đáp án đúng là: B

⦁$\overrightarrow{a}.\overrightarrow{b}=a_1{b}_1+a_2{b}_2$.

Do đó phương án A sai.

⦁ Ta có $\overrightarrow{a}+\overrightarrow{b}=\left(a_1+b_1;a_2+b_2\right)$$\overrightarrow{x}=\overrightarrow{a}+\overrightarrow{b}$.

Vì vậy phương án B đúng.

⦁ $\overrightarrow{a}-\overrightarrow{b}=\left(a_1-b_1;a_2-b_2\right)$.

Do đó phương án C sai.

⦁ $k\overrightarrow{a}=\left(k{a}_1;k{a}_2\right)\left(k\in ℝ\right)$.

Do đó phương án D sai.

Vậy ta chọn phương án B.

Câu 23.

Hướng dẫn giải

Đáp án đúng là: D

Ta có $\frac{1}{2}\overrightarrow{u}=\left(\frac{1}{2}.3;\frac{1}{2}.\left(-6\right)\right)$.

Suy ra $\frac{1}{2}\overrightarrow{u}=\left(\frac{3}{2};-3\right)$.

Vậy ta chọn phương án D.

Câu 24.

Hướng dẫn giải

Đáp án đúng là: B

Phương trình tham số của d: $\left\{\begin{array}{l}x=2+3t\\ y=-3-t\end{array}\right.$

Suy ra đường thẳng d có một vectơ chỉ phương là $\overrightarrow{u}=\left(3;-1\right)$.

Vậy ta chọn phương án B.

Câu 25.

Hướng dẫn giải

Đáp án đúng là: D

Đường thẳng ∆ có một vectơ pháp tuyến là $\overrightarrow{n}=\left(1;-3\right)$.

Suy ra phương án A đúng.

Vectơ pháp tuyến của ∆ có dạng: $k\overrightarrow{n}=\left(k;-3k\right)$.

⦁ Với k = –2, ta có ${\overrightarrow{n}}_1=-2\overrightarrow{n}=\left(-2;6\right)$.

Suy ra phương án B đúng.

Với $k=\frac{1}{3}$, ta có ${\overrightarrow{n}}_2=\frac{1}{3}\overrightarrow{n}=\left(\frac{1}{3};-1\right)$.

Suy ra phương án C đúng.

Vì vậy phương án D sai.

Vậy ta chọn phương án D.

Câu 26.

Hướng dẫn giải

Đáp án đúng là: C

Ta có $\overrightarrow{AC}=\left(-3;-4\right)$.

Vì BH ⊥ AC nên BH nhận $\overrightarrow{AC}=\left(-3;-4\right)$ làm vectơ pháp tuyến.

Đường cao BH đi qua điểm B(–6; –1) và có vectơ pháp tuyến $\overrightarrow{AC}=\left(-3;-4\right)$.

Suy ra phương trình BH: –3(x + 6) – 4(y + 1) = 0.

⇔ –3x – 4y – 22 = 0.

⇔ 3x + 4y + 22 = 0.

Vậy ta chọn phương án C.

Câu 27.

Hướng dẫn giải

Đáp án đúng là: B

Ta có A ∈ AM.

Suy ra tọa độ A(1 + 3t; –2 – 7t).

Lại có A ∈ AH.

Suy ra 2(1 + 3t) + 5(–2 – 7t) + 66 = 0.

Do đó –29t + 58 = 0.

Vì vậy –29t = –58.

Khi đó t = 2.

Suy ra tọa độ A(7; –16).

Gọi I là trung điểm của cạnh AB.

Suy ra$\left\{\begin{array}{l}{x}_I=\frac{x_A+x_B}{2}=\frac{7+4}{2}=\frac{11}{2}\\ y_I=\frac{y_A+y_B}{2}=\frac{-16-3}{2}=-\frac{19}{2}\end{array}\right.$

Khi đó tọa độ $I\left(\frac{11}{2};-\frac{19}{2}\right)$.

Ta có $\overrightarrow{AB}=\left(-3;13\right)$.

Đường trung trực d của cạnh AB đi qua điểm $I\left(\frac{11}{2};-\frac{19}{2}\right)$ và có vectơ pháp tuyến $\overrightarrow{AB}=\left(-3;13\right)$.

Suy ra phương trình d:$-3\left(x-\frac{11}{2}\right)+13\left(y+\frac{19}{2}\right)=0$.

⇔ 3x – 13y – 140 = 0.

Vậy ta chọn phương án B.

Câu 28.

Hướng dẫn giải

Đáp án đúng là: C

Cho đường thẳng d₁, d₂ có vectơ pháp tuyến lần lượt là ${\overrightarrow{n}}_1=\left(a;b\right),{\overrightarrow{n}}_2=\left(c;d\right)$.

Khi đó ta có $\cos \left(d_1,d_2\right)=\frac{\left|{\overrightarrow{n}}_1.{\overrightarrow{n}}_2\right|}{\left|{\overrightarrow{n}}_1\right|.\left|{\overrightarrow{n}}_2\right|}=\frac{\left|ac+bd\right|}{\sqrt{a^2+b^2}.\sqrt{c^2+d^2}}$.

Vậy ta chọn phương án C.

Câu 29.

Hướng dẫn giải

Đáp án đúng là: A

Ta có $d_1:\frac{x}{2}-\frac{y}{3}=1\iff 3x-2y-6=0$.

Ta có:

⦁ Đường thẳng d₁ có vectơ pháp tuyến ${\overrightarrow{n}}_1=\left(3;-2\right)$.

⦁ Đường thẳng d₂ có vectơ pháp tuyến${\overrightarrow{n}}_2=\left(6;-4\right)$.

Vì $\frac{3}{6}=\frac{-2}{-4}$ nên${\overrightarrow{n}}_1$ cùng phương với ${\overrightarrow{n}}_2$ (1)

Chọn A(2; 0) ∈ d₁.

Thế tọa độ A(2; 0) vào phương trình d₂, ta được: 6.2 – 4.0 – 8 = 4 ≠ 0.

Suy ra A(2; 0) ∉ d₂     (2)

Từ (1), (2), ta suy ra d₁ // d₂.

Vậy ta chọn phương án A.

Câu 30.

Hướng dẫn giải

Đáp án đúng là: C

Phương trình đường tròn (C) có dạng (x – a)² + (y – b)² = R², với tâm I(a; b) và bán kính R.

Khi đó tâm I(2; –5).

Vì vậy I ≡ F.

Do đó ta chọn phương án C.

Câu 31.

Hướng dẫn giải

Đáp án đúng là: D

Ta có$R=IB=\sqrt{{\left(2-1\right)}^2+{\left(6-4\right)}^2}=\sqrt{5}$.

Đường tròn có tâm I(1; 4) và có bán kính $R=\sqrt{5}$ có phương trình là:

(x – 1)² + (y – 4)² = 5.

Vậy ta chọn phương án D.

Câu 32.

Hướng dẫn giải

Đáp án đúng là: B

Đường tròn (C) có tâm I(2; 2), bán kính R = 3.

Gọi d là tiếp tuyến cần tìm có vectơ pháp tuyến $\overrightarrow{n}=\left(A;B\right)$.

Vì d đi qua điểm A(5; –1) nên phương trình d có dạng: A(x – 5) + B(y + 1) = 0.

⇔ Ax + By – 5A + B = 0.

Vì d là tiếp tuyến của (C) nên ta có d(I, d) = R.

$\iff \frac{\left|A.2+B.2-5A+B\right|}{\sqrt{A^2+B^2}}=3$

$\iff \left|-3A+3B\right|=3\sqrt{A^2+B^2}$

⇔ 9A² – 18AB + 9B² = 9(A² + B²)

⇔ AB = 0.

⇔ A = 0 hoặc B = 0.

Với A = 0, ta chọn B = 1.

Suy ra phương trình d: y + 1 = 0 ⇔ y = –1.

Với B = 0, ta chọn A = 1.

Suy ra phương trình d: x – 5 = 0 ⇔ x = 5.

Vậy có 2 tiếp tuyến thỏa mãn yêu cầu bài toán có phương trình là: y = –1 hoặc x = 5.

Do đó ta chọn phương án B.

Câu 33.

Hướng dẫn giải

Đáp án đúng là: A

Cho hai điểm F₁, F₂ cố định có khoảng cách F₁F₂ = 2c (c > 0).

Đường hypebol là tập hợp các điểm M sao cho |MF₁ – MF₂| = 2a, trong đó a > 0 và a < c.

Hai điểm F₁ và F₂ được gọi là hai tiêu điểm của hypebol.

Vậy ta chọn phương án A.

Câu 34.

Hướng dẫn giải

Đáp án đúng là: D

Phương trình chính tắc của parabol (P) có dạng: y = 2px (p > 0).

Ta có 2p = 5. Suy ra $p=\frac{5}{2}$.

Khi đó $\frac{p}{2}=\frac{5}{4}$.

Vậy tiêu điểm của parabol (P) là $F\left(\frac{5}{4};0\right)$.

Do đó ta chọn phương án D.

Câu 35.

Hướng dẫn giải

Đáp án đúng là: A

Ta có 9x² + 36y² – 144 = 0

⇔ 9x² + 36y² = 144

$\iff \frac{x^2}{144.\frac{1}{9}}+\frac{y^2}{144.\frac{1}{36}}=1$$\iff \frac{x^2}{16}+\frac{y^2}{4}=1$.

Ta có $\left\{\begin{array}{l}{a}^2=16\\ b^2=4\end{array}\right.\iff \left\{\begin{array}{l}a=4\\ b=2\end{array}\right.$

Suy ra c² = a² – b² = 16 – 4 = 12.

Khi đó $c=\sqrt{12}=2\sqrt{3}$.

Vì vậy tỉ số $\frac{c}{a}=\frac{2\sqrt{3}}{4}=\frac{\sqrt{3}}{2}$.

Vậy ta chọn phương án A.

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1,0 điểm)

Hướng dẫn giải

Ta có cách xếp 8 bạn học sinh vào hai dãy ghế có 8 ghế là hoán vị của 8 nên $n\left(\Omega \right)=8!=40320$ cách xếp.

Gọi A là biến cố bất cứ hai học sinh nào ngồi đối diện nhau khác trường với nhau.

Ta có sơ đồ sau:

Ở ghế 1: có 8 cách chọn học sinh ngồi vào ghế

Ở ghế 5: có 4 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).

Ở ghế 2: có 6 cách chọn học sinh ngồi vào ghế

Ở ghế 6: có 3 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).

Ở ghế 3: có 4 cách chọn học sinh ngồi vào ghế

Ở ghế 7: có 2 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).

Ở ghế 4: có 2 cách chọn học sinh ngồi vào ghế

Ở ghế 8: có 1 cách chọn học sinh ngồi vào ghế (khác trường với học sinh ghế 1).

Suy ra: n(A) = 8.4.6.3.4.2.2.1 = 9 216 cách xếp sao cho bất cứ hai học sinh nào ngồi cạnh nhau hoặc đối diện nhau khác trường với nhau.

Vì vậy $P\left(A\right)=\frac{9216}{40320}=\frac{8}{35}$.

Câu 2. (1,0 điểm)

Hướng dẫn giải

Sản lượng lúa trung bình là:

$\overline{x}=\frac{20.5+21.8+22.11+23.10+24.6}{40}=22,1$.

Mẫu số liệu có 40 giá trị là số chẵn nên trung vị bằng trung bình cộng của giá trị thứ 20 và 21 nên ta có: $Q_2=\frac{22+22}{2}=22$.

Nửa số liệu bên trái có 20 giá trị là số chẵn nên tứ phân vị thứ nhất bằng trung bình cộng của giá trị thứ 10 và 11 nên ta có: $Q_2=\frac{21+21}{2}=21$.

Nửa số liệu bên phải có 20 giá trị là số chẵn nên tứ phân vị thứ ba bằng trung bình cộng của giá trị thứ 30 và 31 nên ta có: $Q_3=\frac{23+23}{2}=23$.

Vậy khoảng tứ phân vị ${\Delta }_Q=Q_3-Q_1=23-21=2$.

Câu 3. (1,0 điểm)

Hướng dẫn giải

Ta có (C): x² + y² – 2x + 2y – 2 = 0

⇔ (x – 1)² + (y + 1)² = 4

Khi đó tâm của đường tròn (C) là I(1; – 1) và R = 2.

a) Vì đường thẳng (∆) song song với (d) nên (∆) có dạng 4x – 3y + c = 0 .

Ta có đường thẳng (∆) tiếp xúc với (C) nên:

d(I, ∆) = $\frac{\left|4.1-3.\left(-1\right)+c\right|}{\sqrt{4^2+{\left(-3\right)}^2}}=\frac{\left|c+7\right|}{5}=2$

$\iff \left|c+7\right|=10$

$\iff \left[\begin{array}{l}c+7=10\\ c+7=-10\end{array}\right.$

b) Gọi phương trình đường thẳng (d) có dạng y = ax + b (a ≠ 0).

A(3; 2) thuộc (d) nên ta có: 3a + b = 2 ⇔ b = 2 – 3a (1).

Ta có đường thẳng (d) tiếp xúc với (C) nên:

d(I, (d)) = $\frac{\left|a.1-\left(-1\right)+b\right|}{\sqrt{a^2+1^2}}=\frac{\left|a+b+1\right|}{\sqrt{a^2+1}}=2$

$\iff \left|a+b+1\right|=2\sqrt{a^2+1}$

$\iff \left|a+2-3a+1\right|=2\sqrt{a^2+1}$

$\iff \left|3-2a\right|=2\sqrt{a^2+1}$

$\iff 9-12a+4a^2=4\left(a^2+1\right)$

$\iff -12a=-5$

$\iff a=\frac{5}{12}$ (thỏa mãn điều kiện)

$\Rightarrow b=2-3a=2-3.\frac{5}{12}=\frac{3}{4}$

Vậy phương trình đường thẳng (d) cần tìm là: 5x – 12y + 9 = 0.

c) Giả tử từ M ta vẽ được hai tiếp tuyến MA, MB với đường tròn (C) tại A và B.

Xét tứ giác MAIB, có: $\widehat{MAI}=\widehat{MBI}=\widehat{AMB}=90°$ nên MAIB là hình chữ nhật.

Mà IA = IB (= R) nên MAIB là hình vuông.

Do đó IM = $2\sqrt{2}$.

Vì M thuộc (d’): x – 2y – 1 = 0 nên M(1 + 2t; t).

$\Rightarrow \overrightarrow{IM}\left(2t;t+1\right)$ 

$\Rightarrow \left|\overrightarrow{IM}\right|=\sqrt{4t^2+{\left(t+1\right)}^2}=\sqrt{5t^2+2t+1}=2\sqrt{2}$

$\iff 5t^2+2t+1=8$

$\iff 5t^2+2t-7=0$

$\iff \left[\begin{array}{l}t=1\\ t=-\frac{7}{5}\end{array}\right.$

Vậy có hai điểm M thỏa mãn yêu cầu bài toán là: M(2; 2) và $M\left(-\frac{14}{5};-\frac{2}{5}\right)$.

Bộ 20 đề thi học kì 2 Toán lớp 10 Kết nối tri thức có đáp án năm 2024 - Đề 3

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 3)

I. PHẦN TRẮC NGHIỆM (7 điểm)

Câu 1. Giá trị x nào sau đây là nghiệm của phương trình $\sqrt{2x^2+3x-5}=x+1$?

A. x = –3;

B. x = 2;

C. Cả A và B đều đúng;

D. Cả A và B đều sai.

Câu 2. Tập nghiệm của bất phương trình (2x – 5)(x + 2) ≥ x² – 4 là:

A. [–2; 3);

B. (–∞; –2) ∪ (3; +∞).;

C. ℝ;

D. (–∞; –2] ∪ [3; +∞).

Câu 3. Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?

A. 3x² – 12x + 1 ≤ 0;

B. 2x³ + 5 > 0;

C. x² + x – 1 = 0;

D. –x + 7 > 0.

Câu 4. Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0). Khẳng định nào sau đây đúng?

A. Nếu ∆ > 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ;

B. Nếu ∆ < 0 thì f(x) luôn trái dấu với hệ số a, ∀x ∈ ℝ;

C. Nếu ∆ = 0 thì f(x) luôn cùng dấu với hệ số a, ∀x ∈ ℝ \ $\left(-\frac{b}{2a}\right)$;

D. Nếu ∆ < 0 thì f(x) luôn cùng dấu với hệ số b, ∀x ∈ ℝ.

Câu 5. Cho kiểu gen AaBb. Giả sử quá trình giảm phân tạo giao tử bình thường và không xảy ra đột biến. Sơ đồ hình cây biểu thị sự hình thành giao tử được biểu diễn như hình bên.

Từ sơ đồ cây, số loại giao tử của kiểu gen AaBb là:

A. 4;

B. 2;

C. 8;

D. 16.

Câu 6. Trong một hộp chứa 6 quả cầu trắng được đánh số từ 1 đến 6 và ba quả cầu đen được đánh số 7; 8; 9. Có bao nhiêu cách chọn một trong các quả cầu ấy?

A. 27;

B. 9;

C. 6;

D. 3.

Câu 7. Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:

A. 24;

B. 480;

C. 48;

D. 60.

Câu 8. Cho tập hợp X gồm n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Một chỉnh hợp chập k của n phần tử là:

A. Một kết quả bất kì của sự sắp xếp k phần tử bất kì của tập hợp X;

B. Một kết quả của việc lấy k phần tử từ n phần tử của tập X và sắp xếp chúng theo một thứ tự nào đó;

C. Một số được tính bởi công thức: n(n – 1)(n – 2)…(n – k + 1);

D. Một kết quả của việc lấy k phần tử từ n phần tử của tập X.

Câu 9. Giá trị của $A_{12}^4$ bằng:

A. 12.11.10.9.8.7.6.5.4;

B. 4.3.2.1;

C. 12.11.10.9;

D. 8!.

Câu 10. Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là

A. 60;

B. 180;

C. 330;

D. 90.

Câu 11. Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + 2b)⁵ bằng

A. 4;

B. 5;

C. 6;

D. 7.

Câu 12. Số hạng chứa x³y trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là:

A. 3x³y;

B. 5x³y;

C. 10x³y;

D. 4x³y.

Câu 13. Số hạng không chứa x trong khai triển $P\left(x\right)={\left(x^3-\frac{1}{x^2}\right)}^5$ (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:

A. 3;

B. 6;

C. 4;

D. 5.

Câu 14. Tổng $S=C_5^0+3C_5^1+3^2{C}_5^2+3^3{C}_5^3+3^4{C}_5^4+3^5{C}_5^5$ bằng:

A. S = 3⁵;

B. S = 2⁵;

C. S = 3.2⁵;

D. S = 4⁵.

Câu 15. Trong mặt phẳng tọa độ Oxy cho $\overrightarrow{a}=\left(3;4\right)$. Độ dài của vectơ $\overrightarrow{a}$ là:

Câu 16. Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 5) và B(6; 7). Tọa độ C là trung điểm của AB là

A. C = (4; 6);

B. C = (5; 6);

C. C = (4; 5);

D. C = (5; 6);

Câu 17. Trong mặt phẳng tọa độ Oxy, cho $\overrightarrow{OA}=\left(2;10\right)$. Đâu là tọa độ của điểm A?

A. (0; 0);

B. (10; 2);

C. (‒ 10; ‒ 2);

D. (2; 10).

Câu 18. Trong mặt phẳng tọa độ Oxy cho 4 điểm A(1; 2), B(2; 3), C(1; ‒1) và D(4; 5). Khẳng định nào là đúng?

A. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ cùng hướng;

B. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ ngược hướng;

C. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ vuông góc với nhau;

D. $\overrightarrow{AB}$ và $\overrightarrow{CD}$ tạo với nhau một góc 30°.

Câu 19. Phương trình tham số của đường thẳng nào sau đâycó vectơ chỉ phương $\overrightarrow{u}=\left(1;3\right)?$

A. $\left\{\begin{array}{l}x=t+1\\ y=3t+2\end{array}\right.$;

B. $\left\{\begin{array}{l}x=t+1\\ y=2t+3\end{array}\right.$;

C. ;$\left\{\begin{array}{l}x=t+2\\ y=t+3\end{array}\right.$

D. $\left\{\begin{array}{l}x=t+3\\ y=2t+1\end{array}\right.$.

Câu 20. Góc giữa 2 đường thẳng có thể có số đo nào sau đây?

A. 135°;

B. 67°;

C. 91°;

D. 180°.

Câu 21. Phương trình đường thẳng d có vectơ chỉ phương $\overrightarrow{u}=\left(1;3\right)$ và đi qua điểm M(3; 4) là

A. 3x – y – 5 = 0;

B. x + 3y – 15 =0;

C. x + 3y + 15 = 0;

D. 3x – y + 15 = 0.

Câu 22. Đường thẳng d đi qua 2 điểm A(1; 3) và B(2; 5). Viết phương trình đoạn chắn của đường thẳng d.

A. $\frac{x}{-\frac{1}{2}}-\frac{y}{1}=1$;

B. $\frac{x}{-2}+\frac{y}{1}=1$;

C. $\frac{x}{-\frac{1}{2}}+\frac{y}{1}=1$;

D. $\frac{x}{2}+\frac{y}{1}=1$.

Câu 23. Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M(x₀; y₀) nằm trên đường tròn có dạng:

A. (a – x₀)(x – x₀) – (b – y₀)(y – y₀) = 0;

B. (a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0;

C. (a + x₀)(x – x₀) – (b + y₀)(y – y₀) = 0;

D. (a + x₀)(x – x₀) + (b + y₀)(y – y₀) = 0.

Câu 24. Tiếp tuyến của đường tròn có tính chất nào sau đây?

A. Cắt đường tròn tại 2 điểm phân biệt;

B. Tiếp tuyến có vectơ chỉ phương là vectơ nối giữa tâm và tiếp điểm;

C. Tiếp tuyến có vectơ pháp tuyến là vectơ nối giữa tâm và tiếp điểm;

D. Cả A, B, C đều đúng.

Câu 25. Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?

A. x² + y² + 2x – 4y + 9 = 0;

B. x² + y² – 6x + 4y + 13 = 0;

C. 2x² + 2y² – 8x – 4y + 2 = 0;

D. 5x² + 4y² + x – 4y + 1 = 0.

Câu 26. Cho phương trình Hypebol $\frac{x^2}{16}-\frac{y^2}{9}=1$. Độ dài trục thực của Hypebol đó là:

A. 3;

B. 4;

C. 6;

D. 8.

Câu 27. Đường chuẩn của Parabol y² = 14x là:

A. $x+\frac{7}{2}=0;$

B.$x-\frac{7}{2}=0;$

C.$x+7=0;$

D. $x-7=0.$

Câu 28. Viết phương trình chính tắc của Elip có độ dài trục lớn và trục nhỏ lần lượt là 20 và 10.

A. $\frac{x^2}{20}+\frac{y^2}{10}=1$ ;

B. $\frac{x^2}{{20}^2}+\frac{y^2}{{10}^2}=1$;

C. $\frac{x^2}{{10}^2}+\frac{y^2}{5^2}=1$;

D. $\frac{x^2}{20}+\frac{y^2}{10}=0$.

Câu 29. Viết phương trình đường tròn tâm I đi qua 3 điểm A(1; 1), B(2; 3) và C(4; 6).

A. x² + y² – 5x + y + 26 = 0;

B. x² + y² – 4x + 17y + 26 = 0;

C. x² + y² – 45x + 17y + 26 = 0;

D. x² + y² – 5x + 27y + 56 = 0.

Câu 30. Một hoạt động mà ta không thể biết trước được kết quả của nó thì được gọi là:

A. Không gian mẫu;

B. Phép thử;

C. Phép thử ngẫu nhiên;

D. Cả B, C đều đúng.

Câu 31. Biến cố là:

A. Một hoạt động mà ta không thể biết trước được kết quả của nó;

B. Tập con của không gian mẫu;

C. Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên;

D. Một kết quả thuận lợi.

Câu 32. Cho 3 hộp, mỗi hộp đựng 5 cái thẻ được đánh số từ 1 đến 5. Rút ngẫu nhiên từ mỗi hộp một tấm thẻ. Biến cố nào sau đây là biến cố chắc chắn?

A. X: “Tổng các số ghi trên ba tấm thẻ rút ra đều lớn hơn hoặc bằng 3”;

B. Y: “Tổng các số ghi trên ba tấm thẻ rút ra không nhỏ hơn 4”;

C. Z: “Tổng các số ghi trên ba tấm thẻ rút ra bằng 8”;

D. T: “Tổng các số ghi trên ba tấm thẻ luôn lớn hơn 15”.

Câu 33. Xác suất của biến cố H được xác định bởi công thức:

A. P(H) = n(H);

B. $P\left(H\right)=\frac{n\left(\Omega \right)}{n\left(H\right)}$;

C. P(H) = n(H).n(Ω);

D. $P\left(H\right)=\frac{n\left(H\right)}{n\left(\Omega \right)}$.

Câu 34. Có ba chiếc hộp. Mỗi hộp chứa 5 tấm thẻ được đánh số từ 1 đến 5. Lấy ngẫu nhiên từ mỗi hộp một thẻ rồi cộng các số trên 3 tấm thẻ vừa rút ra lại với nhau. Xác suất để kết quả thu được là số chẵn là:

A. $\frac{1}{6}$;

B. $\frac{99}{125}$;

C. $\frac{1}{2}$;

D. $\frac{26}{125}$.

Câu 35. Xét các số tự nhiên gồm 5 chữ số khác nhau được lập từ các số 1; 3; 5; 7; 9. Xác suất để tìm được một số không có dạng $\overline{135xy}$ là:

A. $\frac{5}{6}$;

B. $\frac{1}{60}$;

C. $\frac{59}{60}$;

D. $\frac{1}{6}$.

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1 điểm) Trong mặt phẳng Oxy, cho hai điểm A(3; 1) và B(– 2; 4). Viết phương trình đường tròn (C) có tâm I thuộc trục hoành và đi qua hai điểm A, B.

Câu 2. (1 điểm) Hai hộp chứa các quả cầu. Hộp thứ nhất chứa 3 quả đen và 2 quả trắng, hộp thứ hai chứa 4 quả đen và 6 quả trắng.

a) Lấy ngẫu nhiên từ hộp thứ nhất 1 quả. Tính xác suất để lấy được 1 quả đen.

b) Lấy ngẫu nhiên từ mỗi hộp một quả. Tính xác suất để lấy được 2 quả cùng màu.

Câu 3. (1 điểm) Có 5 bưu thiếp khác nhau và 6 bì thư khác nhau. Cần chọn 3 bưu thiếp bỏ vào 3 bì thư, mỗi bì thư một bưu thiếp và gửi cho 3 người bạn mỗi bạn một bưu thiếp. Hỏi có mấy cách thực hiện?

HƯỚNG DẪN ĐÁP ÁN

I. PHẦN TRẮC NGHIỆM (7 điểm)

BẢNG ĐÁP ÁN

1. B	2. D	3. A	4. C	5. A	6. B	7. A
8. B	9. C	10. A	11. B	12. C	13. C	14. D
15. A	16. A	17. D	18. A	19. A	20. B	21. A
22C	23. B	24. C	25. C	26. D	27. A	28. C
29. C	30. D	31. B	32. A	33. D	34. D	35. C

HƯỚNG DẪN CHI TIẾT

Câu 1.

Hướng dẫn giải

Đáp án đúng là: B

Bình phương hai vế của phương trình đã cho, ta được:

2x² + 3x – 5 = (x + 1)²

⇒ 2x² + 3x – 5 = x² + 2x + 1

⇒ x² + x – 6 = 0

⇒ x = 2 hoặc x = –3.

Với x = 2, ta có $\sqrt{{2.2}^2+3.2-5}=2+1$ (đúng)

Với x = –3, ta có $\sqrt{2{\left(-3\right)}^2+3.\left(-3\right)-5}=-3+1$ (sai)

Vì vậy khi thay lần lượt các giá trị x = 2 và x = –3 vào phương trình đã cho, ta thấy chỉ có x = 2 thỏa mãn.

Vậy nghiệm của phương trình đã cho là x = 2.

Ta chọn phương án B.

Câu 2.

Hướng dẫn giải

Đáp án đúng là: D

Ta có (2x – 5)(x + 2) ≥ x² – 4.

⇔ 2x² – x – 10 ≥ x² – 4.

⇔ x² – x – 6 ≥ 0.

Tam thức bậc hai f(x) = x² – x – 6 có ∆ = (–1)² – 4.1.(–6) = 25 > 0.

Suy ra f(x) có hai nghiệm phân biệt là:

$x_1=\frac{1-\sqrt{25}}{2}=-2;x_2=\frac{1+\sqrt{25}}{2}=3.$

Ta lại có a = 1 > 0.

Vì vậy:

⦁ f(x) dương với mọi x thuộc hai khoảng (–∞; –2) và (3; +∞);

⦁ f(x) âm với mọi x thuộc khoảng (–2; 3);

⦁ f(x) = 0 khi x = –2 hoặc x = 3.

Vậy bất phương trình x² – x – 6 ≥ 0 có tập nghiệm là (–∞; –2] ∪ [3; +∞).

Do đó ta chọn phương án D.

Câu 3.

Hướng dẫn giải

Đáp án đúng là: A

Bất phương trình bậc hai một ẩn x là bất phương trình có một trong các dạng:

ax² + bx + c ≤ 0; ax² + bx + c < 0; ax² + bx + c ≥ 0; ax² + bx + c > 0 với a ≠ 0.

Trong bốn phương án A, B, C, D, ta thấy chỉ có phương án A là có dạng bất phương trình bậc hai một ẩn dạng ax² + bx + c ≤ 0 với a = 3, b = – 12 và c = 1.

Ta chọn phương án A.

Câu 4.

Hướng dẫn giải

Đáp án đúng là: C

Cho tam thức bậc hai f(x) = ax² + bx + c (a ≠ 0), ta có:

⦁ Nếu ∆ < 0 thì f(x) cùng dấu với a với mọi giá trị x.

Do đó phương án B, D đều sai.

⦁ Nếu ∆ = 0 và $x_0=-\frac{b}{2a}$ là nghiệm kép của f(x) thì f(x) cùng dấu với a với mọi x ≠ x₀.

Do đó phương án C đúng.

⦁ Nếu ∆ > 0 và x₁, x₂ là hai nghiệm của f(x) (x₁ < x₂) thì f(x) trái dấu với a với mọi x trong khoảng (x₁; x₂); f(x) cùng dấu với a với mọi x thuộc hai khoảng (–∞; x₁); (x₂; +∞).

Do đó phương án A sai.

Vậy ta chọn phương án C.

Câu 5.

Hướng dẫn giải

Đáp án đúng là: A

Từ sơ đồ cây, ta thấy có 4 kết quả có thể xảy ra.

Do đó số loại giao tử của kiểu gen AaBb là 4.

Vậy ta chọn phương án A.

Câu 6.

Hướng dẫn giải

Đáp án đúng là: B

Việc chọn một trong các quả cầu trong hộp có hai phương án thực hiện:

Phương án 1: Chọn một quả cầu màu trắng, có 6 cách chọn.

Phương án 2: Chọn một quả cầu màu đen, có 3 cách chọn.

Theo quy tắc cộng, ta có tất cả 6 + 3 = 9 cách chọn một quả cầu trong hộp.

Vậy ta chọn phương án B.

Câu 7.

Hướng dẫn giải

Đáp án đúng là: A

Việc chọn một đồ vật duy nhất có ba phương án thực hiện:

Phương án 1: Chọn một cây bút chì, có 8 cách chọn.

Phương án 2: Chọn một cây bút bi, có 6 cách chọn.

Phương án 3: Chọn một cuốn tập, có 10 cách chọn.

Theo quy tắc cộng, ta có tất cả 8 + 6 + 10 = 24 cách chọn một đồ vật duy nhất.

Vậy ta chọn phương án A.

Câu 8.

Hướng dẫn giải

Đáp án đúng là: B

Mỗi cách lấy k phần tử của tập X và sắp xếp chúng theo một thứ tự gọi là một chỉnh hợp chập k của n phần tử đó.

Vậy ta chọn phương án B.

Câu 9.

Hướng dẫn giải

Đáp án đúng là: C

Ta có null.

Do đó ta chọn phương án C.

Câu 10.

Hướng dẫn giải

Đáp án đúng là: A

Công việc chọn học sinh tham gia cuộc thi có 3 công đoạn:

Công đoạn 1: Chọn 3 học sinh giỏi lớp 12.

Mỗi cách chọn 3 học sinh giỏi trong số 4 học sinh giỏi lớp 12 là một tổ hợp chập 3 của 4 phần tử.

Do đó số cách chọn 3 học sinh lớp 12 là: $C_4^3$ (cách).

Công đoạn 2: Chọn 1 học sinh giỏi lớp 11.

Mỗi cách chọn 1 học sinh giỏi trong số 3 học sinh giỏi lớp 11 là một tổ hợp chập 1 của 3 phần tử.

Do đó số cách chọn 1 học sinh lớp 11 là: $C_3^1$ (cách).

Công đoạn 3: Chọn 1 học sinh giỏi lớp 10.

Mỗi cách chọn 1 học sinh giỏi trong số 5 học sinh giỏi lớp 10 là một tổ hợp chập 1 của 5 phần tử.

Do đó số cách chọn 1 học sinh lớp 10 là: $C_5^1$ (cách).

Vậy theo quy tắc nhân, ta có tất cả $C_4^3.C_3^1.C_5^1=60$ cách chọn 5 học sinh giỏi của trường đó.

Ta chọn phương án A.

Câu 11.

Hướng dẫn giải

Đáp án đúng là: B

Ta có tổng số mũ của a, b trong mỗi hạng tử khi khai triển (a + b)ⁿ luôn bằng n.

Vậy tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (a + 2b)⁵ bằng 5.

Câu 12.

Hướng dẫn giải

Đáp án đúng là: C

Ta có:

${\left(xy+\frac{1}{y}\right)}^5$

$=C_5^0{\left(xy\right)}^5{\left(\frac{1}{y}\right)}^0+C_5^1{\left(xy\right)}^4{\left(\frac{1}{y}\right)}^1+C_5^2{\left(xy\right)}^3{\left(\frac{1}{y}\right)}^2$

$+C_5^3{\left(xy\right)}^2{\left(\frac{1}{y}\right)}^3+C_5^4{\left(xy\right)}^1{\left(\frac{1}{y}\right)}^4+C_5^5{\left(xy\right)}^0{\left(\frac{1}{y}\right)}^5$

$=x^5{y}^5+5x^4{y}^4.\frac{1}{y}+10x^3{y}^3.\frac{1}{y^2}+10x^2{y}^2.\frac{1}{y^3}+5xy.\frac{1}{y^4}+\frac{1}{y^5}$

$=x^5{y}^5+5x^4{y}^3+10x^{3}y+10x^2.\frac{1}{y}+5x.\frac{1}{y^3}+\frac{1}{y^5}$

Vậy số hạng chứa x³y trong khai triển ${\left(xy+\frac{1}{y}\right)}^5$ là 10x³y.

Câu 13.

Hướng dẫn giải

Đáp án đúng là: C

Theo nhị thức Newton, ta có:

$P\left(x\right)={\left(x^3-\frac{1}{x^2}\right)}^5$

$={\left(x^3\right)}^5+5.{\left(x^3\right)}^4.\left(-\frac{1}{x^2}\right)+10.{\left(x^3\right)}^3.{\left(-\frac{1}{x^2}\right)}^2$$+10.{\left(x^3\right)}^2.{\left(-\frac{1}{x^2}\right)}^3+5.x^3.{\left(-\frac{1}{x^2}\right)}^4+{\left(-\frac{1}{x^2}\right)}^5$

$=x^{15}-5.x^{12}.\frac{1}{x^2}+10.x^9.\frac{1}{x^4}-10.x^6.\frac{1}{x^6}+5.x^3.\frac{1}{x^8}-\frac{1}{x^{10}}$

$=x^{15}-5.x^{10}+10.x^5-10+5.\frac{1}{x^5}-\frac{1}{x^{10}}$

Ta thấy số hạng không chứa x là số hạng thứ 4 (theo chiều số mũ của x giảm dần).

Vậy ta chọn phương án C.

Câu 14.

Hướng dẫn giải

Đáp án đúng là: D

Theo công thức nhị thức Newton, ta có:

${\left(1+x\right)}^5$

$=C_5^0{.1}^5+C_5^1{.1}^4.x+C_5^2{.1}^3.x^2+C_5^3{.1}^2.x^3+C_5^4\mathrm{.1.}{x}^4+C_5^5.x^5$

$=C_5^0+C_5^1.x+C_5^2.x^2+C_5^3.x^3+C_5^4.x^4+C_5^5.x^5$

Cho x = 3, ta có:

${\left(1+3\right)}^5=C_5^0+C_5^1.3+C_5^2{.3}^2+C_5^3{.3}^3+C_5^4{.3}^4+C_5^5{.3}^5$.

Suy ra $S=C_5^0+3C_5^1+3^2{C}_5^2+3^3{C}_5^3+3^4{C}_5^4+3^5{C}_5^5=4^5$.

Vậy ta chọn phương án D.

Câu 15.

Hướng dẫn giải

Đáp án đúng là: A

Độ dài vectơ $\overrightarrow{a}$ là: $\left(\overrightarrow{a}\right)=\sqrt{3^2+4^2}=5$.

Câu 16.

Hướng dẫn giải

Đáp án đúng là: A

Điểm C là trung điểm của đoạn thẳng AB với A(2; 5) và B(6; 7) nên ta có:

$x_C=\frac{x_A+x_B}{2}=\frac{2+6}{2}=4$

$y_C=\frac{y_A+y_B}{2}=\frac{5+7}{2}=6$

Vậy C(4; 6).

Câu 17.

Hướng dẫn giải

Đáp án đúng là: D

Do $\overrightarrow{OA}=\left(2;10\right)$ nên A có tọa độ là (2; 10).

Câu 18.

Hướng dẫn giải

Đáp án đúng là: A

Ta có: A(1; 2), B(2; 3) nên $\overrightarrow{AB}=\left(2-1;3-2\right)=\left(1;1\right)$;

C(1; ‒1), D(4; 5) nên $\overrightarrow{CD}=\left(4-1;5+1\right)=\left(3;3\right)$.

Ta thấy: $\overrightarrow{CD}=3\overrightarrow{AB}$ nên $\overrightarrow{AB}$ và $\overrightarrow{CD}$cùng hướng.

Câu 19.

Hướng dẫn giải

Đáp án đúng là: A

Đường thẳng có phương trình tham số $\left\{\begin{array}{l}x=t+1\\ y=3t+2\end{array}\right.$$\overrightarrow{u}=\left(1;3\right)$$\left\{\begin{array}{l}x=t+1\\ y=2t+3\end{array}\right.$$\overrightarrow{u}=\left(1;2\right).$$\left\{\begin{array}{l}x=t+2\\ y=t+3\end{array}\right.$ có vectơ chỉ phương là $\overrightarrow{u}=\left(1;1\right).$

Đường thẳng có phương trình tham số $\left\{\begin{array}{l}x=t+3\\ y=2t+1\end{array}\right.$ có vectơ chỉ phương là $\overrightarrow{u}=\left(1;2\right).$<

Vậy ta chọn phương án A.

Câu 20.

Hướng dẫn giải

Đáp án đúng là: B

Góc giữa 2 đường thẳng luôn là một góc nhỏ hơn hoặc bằng 90°.

Do đó chỉ có B là thỏa mãn.

Câu 21.

Hướng dẫn giải

Đáp án đúng là: A

Đường thẳng d có vectơ chỉ phương là $\overrightarrow{u}=\left(1;3\right)$nên có vectơ pháp tuyến là $\overrightarrow{n}=\left(3;-1\right)$.

Đường thẳng d có vectơ pháp tuyến $\overrightarrow{n}=\left(3;-1\right)$ và đi qua điểm M(3; 4) nên có phương trình tổng quát là: 3(x – 3) – 1.(y – 4) = 0 hay 3x – y – 5 = 0.

Vậy ta chọn phương án A.

Câu 22.

Hướng dẫn giải

Đáp án đúng là: C

Đường thẳng d có vectơ chỉ phương là: $\overrightarrow{u}=\overrightarrow{AB}=\left(1;2\right)$

Suy ra đường thẳng d có vectơ pháp tuyến là: $\overrightarrow{n}=\left(2;-1\right)$.

Đường thẳng d có vectơ pháp tuyến $\overrightarrow{n}=\left(2;-1\right)$ và đi qua điểm A(1; 3) nên có phương trình tổng quát là:

2(x – 1) – (y – 3) = 0 hay 2x – y + 1 = 0.

Đường thẳng d cắt 2 trục tọa độ Ox và Oy lần lượt tại M$\left(-\frac{1}{2};0\right)$ và $N\left(0;1\right)$.

Vậy phương trình đoạn chắn của đường thẳng d là: $\frac{x}{-\frac{1}{2}}+\frac{y}{1}=1$.

Câu 23.

Hướng dẫn giải

Đáp án đúng là: B

Phương trình tiếp tuyến của đường tròn tâm I(a; b) tại điểm M($x_0;y_0$) nằm trên đường tròn có dạng: (a – x₀)(x – x₀) + (b – y₀)(y – y₀) = 0.

Vậy ta chọn phương án B.

Câu 24.

Hướng dẫn giải

Đáp án đúng là: C

Tiếp tuyến của đường tròn có vectơ pháp tuyến là vectơ nối giữa tâm và tiếp điểm.

Vậy ta chọn phương án C.

Câu 25.

Hướng dẫn giải

Đáp án đúng là: C

Ta loại phương án D vì không có dạng x² + y² – 2ax – 2by + c = 0.

Xét phương án A: x² + y² + 2x – 4y + 9 = 0 có a = –1, b = 2 và c = 9.

Do đó a² + b² – c = (–1)² + 2² – 9 = –4 < 0 nên loại A.

Xét phương án B: x² + y² – 6x + 4y + 13 = 0 có a = 3; b = –2 và c = 13

Do đó a² + b² – c = 3² + (–2)² – 13 = 0 nên loại B.

Xét phương án C: 2x² + 2y² – 8x – 4y + 2 = 0

$\iff$ x² + y² – 4x – 2y + 1 = 0.

Có a = 2; b = 1 và c = 1.

Do đó a² + b² – c = 2² + 1² – 1 = 4 > 0 nên chọn C.

Vậy ta chọn phương án C.

Câu 26.

Hướng dẫn giải

Đáp án đúng là: D

Từ phương trình Hypebol $\frac{x^2}{16}-\frac{y^2}{9}=1$ ta có a² = 16 và b² = 9

Mà a, b > 0 nên a = 4 và b = 3.

Do đó độ dài trục thực của Hypebol là 2a = 8.

Câu 27.

Hướng dẫn giải

Đáp án đúng là: A

Từ phương trình Parabol y² = 14x ta có 2p = 14 suy ra $\frac{p}{2}=\frac{7}{2}$.

Do đó phương trình đường chuẩn của Parabol là $x+\frac{7}{2}=0.$

Câu 28.

Hướng dẫn giải

Đáp án đúng là: C

Ta có: 2a = 20 và 2b = 10, do đó: a = 10 và b =5

Khi đó ta có phương trình Elip: $\frac{x^2}{{10}^2}+\frac{y^2}{5^2}=1$.

Câu 29.

Hướng dẫn giải

Đáp án đúng là: C

Gọi M, N lần lượt là trung điểm của AB, AC.

Khi đó $M\left(\frac{3}{2};2\right),N\left(\frac{5}{2};\frac{7}{2}\right)$

Đường trung trực d của đoạn thẳng AB là đường thẳng đi qua M và nhận $\overrightarrow{AB}=\left(1;2\right)$ làm vectơ pháp tuyến nên có phương trình:

$x-\frac{3}{2}+2\left(y-2\right)=0\iff 2x+4y-11=0$

Đường trung trực ∆ của đoạn thẳng AC là đường thẳng đi qua N và nhận $\overrightarrow{AC}=\left(3;5\right)$ làm vectơ pháp tuyến nên có phương trình:

$3\left(x-\frac{5}{2}\right)+5\left(y-\frac{7}{2}\right)=0\iff 3x+5y-25=0$

Đường thẳng d cắt đường thẳng ∆ cắt nhau tại điểm $I\left(\frac{45}{2};-\frac{17}{2}\right)$ cách đều ba điểm A, B, C.

Do đó đường tròn đi qua ba điểm A, B, C có tâm $I\left(\frac{45}{2};-\frac{17}{2}\right)$ và bán kính $R^2=I{A}^2={\left(1-\frac{45}{2}\right)}^2+{\left(1+\frac{17}{2}\right)}^2=\frac{1105}{2}$

Ta có ${\left(\frac{45}{2}\right)}^2+{\left(-\frac{17}{2}\right)}^2-\frac{1105}{2}=26$

Khi đó đường tròn (C) có phương trình là:

x² + y² – 45x + 17y + 36 = 0.

Câu 30.

Hướng dẫn giải

Đáp án đúng là: D

⦁ Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu. Do đó phương án A sai.

⦁ Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó. Do đó phương án B, C đúng.

Vậy ta chọn phương án D.

Câu 31.

Hướng dẫn giải

Đáp án đúng là: B

⦁ Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó. Do đó phương án A sai.

⦁ Mỗi tập con của không gian mẫu được gọi là một biến cố. Do đó phương án B đúng.

⦁ Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu. Do đó phương án C sai.

⦁ Một kết quả thuộc biến cố được gọi là kết quả làm cho biến cố xảy ra, hoặc kết quả thuận lợi cho biến cố đó. Do đó phương án D sai.

Vậy ta chọn phương án B.

Câu 32.

Hướng dẫn giải

Đáp án đúng là: A

⦁ Ta thấy mỗi thẻ đều được đánh số từ 1 đến 5, đây là các số đều lớn hơn hoặc bằng 1.

Do đó khi tính tổng các số ghi trên cả ba tấm thẻ, ta sẽ được tổng các số đó đều lớn hơn hoặc bằng 3.

Vì vậy biến cố X là biến cố chắc chắn.

⦁ Ta có thể rút được 3 thẻ đều được ghi số 1.

Khi đó tổng các số ghi trên cả ba tấm thẻ là bằng 3 < 4 và 3 ≠ 8.

Do đó biến cố Y và biến cố Z không phải là biến cố chắc chắn.

⦁ Trong các số từ 1 đến 5, ta thấy số 5 lớn nhất.

Giả sử ba tấm thẻ được rút ra đều được ghi số 5.

Khi đó tổng ba số là 15.

Vì vậy không có 3 thẻ nào có tổng các số ghi trên thẻ cộng lại lớn hơn 15.

Do đó biến cố T là biến cố không thể.

Vậy ta chọn phương án A.

Câu 33.

Hướng dẫn giải

Đáp án đúng là: D

Xác suất của biến cố H là một số, kí hiệu là P(H), được xác định bởi công thức:

$P\left(H\right)=\frac{n\left(H\right)}{n\left(\Omega \right)}$.

Trong đó n(H) và n(Ω) lần lượt kí hiệu số phần tử của tập H và Ω.

Vậy ta chọn phương án D.

Câu 34.

Hướng dẫn giải

Đáp án đúng là: D

⦁ Ta tìm số phần tử của không gian mẫu:

Giai đoạn 1: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ nhất, ta có $C_5^1$ cách chọn.

Giai đoạn 2: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ hai, ta có $C_5^1$ cách chọn.

Giai đoạn 3: Chọn 1 tấm thẻ trong số 5 tấm thẻ ở hộp thứ ba, ta có $C_5^1$ cách chọn.

Theo quy tắc nhân, ta có tất cả $C_5^1.C_5^1.C_5^1=125$ cách chọn.

Do đó n(Ω) = 125.

⦁ Tính số phần tử của biến cố theo yêu cầu bài toán:

Gọi A: “Kết quả thu được là số chẵn”.

Trường hợp 1: 2 thẻ là số lẻ (trong {1; 3; 5}) và 1 thẻ là số chẵn (trong {2; 4}).

Khi đó ta có $C_3^1.C_3^1.C_2^1=18$ cách chọn.

Trường hợp 2: Cả 3 thẻ đều là số chẵn.

Khi đó ta có $C_2^1.C_2^1.C_2^1=8$ cách chọn.

Kết hợp cả hai trường hợp, ta được n(A) = 18 + 8 = 26.

Vậy xác suất của biến cố A là: $P\left(A\right)=\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{26}{125}$.

Ta chọn phương án D.

Câu 35.

Hướng dẫn giải

Đáp án đúng là: C

Số phần tử của không gian mẫu là: n(Ω) = 5! = 120.

Gọi biến cố A: “Số tìm được không có dạng $\overline{135xy}$ ”.

Suy ra biến cố đối của biến cố A là: $\overline{A}$: “Số tìm được có dạng $\overline{135xy}$”.

⦁ x có 2 cách chọn là x = 7 hoặc x = 9.

⦁ y có 1 cách chọn.

Theo quy tắc đếm, ta có $n\left(\overline{A}\right)$ = 1.1.1.2.1 = 2 cách chọn.

Vì vậy xác suất của biến cố $\overline{A}$ là: $P\left(\overline{A}\right)=\frac{n\left(\overline{A}\right)}{n\left(\Omega \right)}=\frac{2}{120}=\frac{1}{60}$.

Ta có $P\left(A\right)+P\left(\overline{A}\right)=1$.

Suy ra $P\left(A\right)=1-P\left(\overline{A}\right)=1-\frac{1}{60}=\frac{59}{60}$.

Vậy ta chọn phương án C.

II. PHẦN TỰ LUẬN (3 điểm)

Câu 1. (1 điểm)

Hướng dẫn giải

Gọi tọa độ điểm I(a; 0).

Khi đó:

$\overrightarrow{AI}\left(a-3;-1\right)\Rightarrow IA=\sqrt{{\left(a-3\right)}^2+1}=\sqrt{a^2-6a+10}$

$\overrightarrow{BI}\left(a+2;-4\right)\Rightarrow IB=\sqrt{{\left(a+2\right)}^2+{\left(-4\right)}^2}=\sqrt{a^2+4a+20}$

Mà IA = IB = R nên $\sqrt{a^2-6a+10}=\sqrt{a^2+4a+20}$

⇒ a² – 6a + 10 = a² + 4a + 20

⇒ – 10a = 10

⇒ a = – 1

Thay vào lại phương trình ta thấy a = -1 thỏa mãn.

Suy ra I(– 1; 0) và $R=IA=\sqrt{{\left(-1\right)}^2-6\left(-1\right)+10}=\sqrt{17}$.

Vì vậy phương trình đường tròn (C) là: (x + 1)² + y² = 17.

Câu 2. (1 điểm)

Hướng dẫn giải

a) Ta có: $n\left(\Omega \right)=C_5^1$

Gọi A là biến cố: “Lấy được một quả màu đen”.

Để lấy được một quả bóng đen từ hộp thứ nhất có: n(A) = $C_3^1$.

Vì vậy xác suất để biến cố A xảy ra là: P(A) = $\frac{n\left(A\right)}{n\left(\Omega \right)}=\frac{C_3^1}{C_5^1}=\frac{3}{5}$.

b) Ta có: $n\left(\Omega \right)=C_5^1{C}_{10}^1$

Gọi B là biến cố: “Lấy được 2 quả cùng màu”.

Các kết quả thuận lợi cho biến cố B được chia làm 2 phương án:

Phương án 1: Hai quả bóng lấy ra đều màu đen có $C_3^1.C_4^1$ cách.

Phương án 2: Hai quả bóng lấy ra đều màu trắng có $C_2^1.C_6^1$ cách.

⇒ n(B) = $C_3^1.C_4^1$.

Vì vậy xác suất để biến cố B xảy ra là: P(B) = $\frac{n\left(B\right)}{n\left(\Omega \right)}=\frac{C_3^1.C_4^1+C_2^1.C_6^1}{C_5^1.C_{10}^1}=\frac{12}{25}$.

Câu 3. (1 điểm)

Hướng dẫn giải

Cách để thực hiện được chia làm 3 công đoạn:

Công đoạn 1: Chọn 3 bưu thiếp có: $C_5^3$ cách.

Công đoạn 2: Ứng 3 bưu thiếp số cách chọn 3 bì thư là: $C_6^3$ cách.

Công đoạn 3: Có 3! Cách để nhét 3 bưu thiếp vào mỗi phong bì tương ứng.

Vậy có: $C_5^3.C_6^3.2!=1200$ cách.

 

Bộ 20 đề thi học kì 2 Toán lớp 10 Kết nối tri thức có đáp án năm 2024 - Đề 4

Phòng Giáo dục và Đào tạo ...

Đề thi Học kì 2 - Kết nối tri thức

Năm học 2023 - 2024

Môn: Toán lớp 10

Thời gian làm bài: 90 phút

(không kể thời gian phát đề)

(Đề số 4)

Phần I: Trắc nghiệm

Câu 1: Đường thẳng d đi qua hai điểm A(8;0), B(0;7) có phương trình là:

Câu 2: Số đo tính theo đơn vị rađian của góc 135^o là:

Câu 3: Tập nghiệm của bất phương trình x² - 3x - 4 < 0

A. (-∞;-1) ∪ (4;+∞) B.(-∞;-1)

C. (4;+∞) D. (-1;4)

Câu 4: Góc giữa hai đường thẳng d: x + y + 2 = 0 và d': y + 1 = 0 có số đo bằng:

A. 90^o B. 60^o

C. 45^o D. 30^o

Câu 5: Đường tròn (C): x² + y² - 4x + 6y - 12 = 0 có tâm I và bán kính R là:

A. I(-2;3), R = 25 B. I(-2;3), R = 5

C. I(2;-3), R = 25 D. I(2;-3), R = 5

Câu 6: Cho đường thẳng Δ: x + 2y + m = 0 và đường tròn (C): x² + y² = 9. Giá trị của m để Δ tiếp xúc với (C) là:

Câu 7: Cho hai điểm M(3;2), N(-1;-4). Đường trung trực của MN có phương trình là:

A. 2x + 3y + 1 = 0 B. 2x + 3y - 1 = 0

C. 2x - 3y + 1 = 0 D. 2x - 3y - 1 = 0

Câu 8: Đường elip 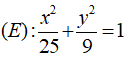 có tâm sai bằng:

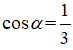
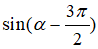
Câu 9: Cho  . Khi đó,  bằng:

Câu 10: Đường elip 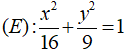 có tiêu cự bằng:

A. √7 B. 2√7

C. 5 D. 10

Câu 11: Cho s⁡inx + cosx = √2. Khi đó sin⁡2 x có giá trị bằng:

A. -1 B. 0

C. 1 D. 2

Câu 12: Tập nghiệm của bất phương trình 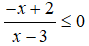 là:

A. (-∞;2] ∪ [3;+∞) B. (-∞;2] ∪ (3;+∞)

C. (-∞;2) ∪ [3;+∞) D. [2;3]

Câu 13: Với mọi số thực α, ta có 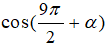 bằng:

A. sin⁡α B. cosα

C. -sin⁡α D. -cosα

Câu 14: Cho 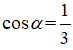 . Khi đó, cos2α nhận giá trị bằng:

Câu 15: Tập nghiệm của bất phương trình |2x-1| < 3x-2 là:

Câu 16: Hàm số 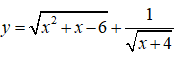 có tập xác định:

A. D = [-4;-3] ∪ [2;+∞) B. D = (-4;+∞)

C. D = (-∞;-3] ∪ [2;+∞) D. D = (-4;-3] ∪ [2;+∞)

Câu 17: Điều tra về số con của 30 gia đình ở khu vực Hà Đông - Hà Nội kết quả thu được như sau:

Giá trị ( số con)	0	1	2	3	4
Tần số	1	7	15	5	2	N = 30

Số trung bình x của mẫu số liệu trên bằng:

A. 1 B. 1,5

C. 2 D. 3

Câu 18: Với a, b là hai số thực tùy ý. Đẳng thức nào sau đây sai?

Câu 19: Giá trị của tham số m để d:x-2y+3=0 và 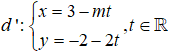 song song với nhau là:

A. m = 1 B. m = -1

C. m = 4 D. m = -4

Câu 20: Cho hypebol 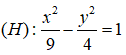 . Diện tích hình chữ nhật cơ sở là:

A. 6 B. 12

C. 18 D. 24

Phần II: Tự luận

Câu 1: Giải các bất phương trình sau:

Câu 2: Cho 

Tính giá trị biểu thức sau:

Câu 3: Trong mặt phẳng với hệ tọa độ Oxy, cho ba điểm A(1;2), B(3;-1), C(-2;1)

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC

b) Viết phương trình đường tròn đường kính AB

Câu 4: Giải phương trình:

Đáp án & Hướng dẫn giải

Phần I: Trắc nghiệm

1	2	3	4	5
A	B	D	C	D
6	7	8	9	10
C	A	C	C	B
11	12	13	14	15
C	B	C	A	D
16	17	18	19	20
D	C	A	C	D

Câu 1: Đáp án: A

Phương trình đoạn chắn đi qua hai điểm A(8;0), B(0;7) là:

Câu 2: Đáp án: B

Số đo tính theo đơn vị rađian của góc 135^o là:

Câu 3: Đáp án: D

x² - 3x - 4 < 0 ⇔ (x + 1)(x - 4) < 0 ⇔ -1 < x < 4

Câu 4: Đáp án: C

Gọi α là góc giữa hai đường thẳng d và d’

Câu 5: Đáp án: D

(C): x² + y² - 4x + 6y - 12 = 0 ⇔ (x - 2)² + (y + 3)² = 25

Vậy đường tròn (C) có I(2;-3), R = 5

Câu 6: Đáp án: C

(C): x² + y² = 9 có I(0;0), R = 3

Để Δ tiếp xúc với đường tròn (C) thì

Câu 7: Đáp án: A

M(3;2), N(-1;-4) 

Gọi I là trung điểm của MN ⇒ I(1;-1)

Đường thẳng trung trực của MN là đường thẳng đi qua I và nhận vecto MN làm vecto pháp tuyến:

MN: -4(x - 1) - 6(y + 1) = 0 ⇔ 2x + 3y + 1 = 0

Câu 8: Đáp án: C

Ta có: 

⇒ a² = 25, b² = 9

Mà a² = b² + c² ⇒ c² = a² - b² = 25 - 9 = 16 ⇒ c = 4

Vậy 

Câu 9: Đáp án: C

Ta có:

Câu 10: Đáp án: B

⇒ a² = 16, b² = 9

Mà c² = a² - b² = 16 - 9 = 7 ⇒ c = √7 ⇒ 2c = 2√7

Câu 11: Đáp án: C

Ta có: s⁡inx + cosx = √2 ⇒ (s⁡inx + cosx)² = 2

⇔ sin²x + 2sin⁡xcos⁡x + cos²⁡ x = 2

⇔ 1 + sin⁡2x = 2

⇔ sin⁡2x = 1

Câu 12: Đáp án: B

Giải bất phương trình 

Ta có bảng xét dấu vế trái của bất phương trình:

Vậy tập nghiệm của bất phương trình là: (-∞;2] ∪ (3;+∞)

Câu 13: Đáp án: C

Ta có:

Câu 14: Đáp án: A

Ta có:

Câu 15: Đáp án: D

Ta có:

Câu 16: Đáp án: D

Hàm số 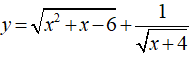 xác định khi và chỉ khi:

Vậy tập xác định của hàm số là: D = (-4;-3] ∪ [2;+∞)

Câu 17: Đáp án: C

Ta có:

Câu 18: Đáp án: A

Ta có: cos2x = cos²x - sin²⁡x

Vậy đáp án A sai

Câu 19: Đáp án: C

Vì d//d'

Câu 20: Đáp án: D

có a² = 9 ⇒ a = 3, b² = 4 ⇒ b = 2

Hình chữ nhật cơ sở của hypebol (H) là hình chữ nhật với độ dài hai cạnh là 6 và 4. Vậy diện tích hình chữ nhật cơ sở là: 6.4 = 24

Phần II: Tự luận

Câu 1:

Giải các bất phương trình sau:

Ta có:

Ta có bảng xét dấu vế trái của bất phương trình:

Vậy tập nghiệm của bất phương trình là:

Ta có:

Vậy tập nghiệm của bất phương trình là:

Câu 2:

Ta có:

Vậy giá trị của P là: 

Câu 3:

a) Viết phương trình tổng quát của AB và tính diện tích tam giác ABC

Phương trình tổng quát của AB là: 3(x - 1) + 2(y - 2) = 0 ⇔ 3x + 2y - 7 = 0

Kẻ CH ⊥ AB, (H ∈ AB)

Diện tích tam giác ABC là:

b) Viết phương trình đường tròn đường kính AB

Gọi I là trung điểm của AB

Đường tròn đường kính AB là đường tròn tâm I bán kính IA:

Câu 4:

Ta thấy:

Áp dụng bất đẳng thức Cô – si ta có:

Cộng vế với vế ta được:

Dấu “=” xảy ra khi và chỉ khi x - 1 = 2 ⇔ x = 3

Vậy x = 3 là nghiệm của phương trình.