Tailieumoi.vn xin giới thiệu Bài tập Toán 5 Chương 3 Bài 105: Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 3 Bài 105: Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật. Mời các bạn đón xem:

Bài tập Toán 5 Bài 105: Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật 

A. Bài tập Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

I. Bài tập trắc nghiệm

Câu 1: Phát biểu nào sau đây là Đúng?

A. Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng một đơn vị đo).

B. Diện tích toàn phần của hình hộp chữ nhật bằng diện tích xung quanh nhân với diện tích hai đáy.

C. Diện tích toàn phần bằng chu vi đáy nhân với chiều cao.

D. Diện tích xung quanh của hình hộp chữ nhật bằng diện tích đáy nhân với chiều cao.

Câu 2: Tính diện tích xung quanh của hình hộp chữ nhật có chiều dài 6dm, chiều rộng 4dm, chiều cao 8dm.

A. $120{\mathrm{dm}}^2$

B. $160{\mathrm{dm}}^2$

C. $130{\mathrm{dm}}^2$

D. $192{\mathrm{dm}}^2$

Câu 3: Một hình hộp chữ nhật có kích thước a, b, c (cùng đơn vị đo) tương ứng với chiều dài, chiều rộng và chiều cao. Công thức tính diện tích toàn phần của hình hộp đó là:

A. $\mathrm{S}=\left(\mathrm{a}+\mathrm{b}\right)\times 2\times \mathrm{c}$

B. $\mathrm{S}=\left(\mathrm{a}\times \mathrm{b}\right)\times 2\times \mathrm{c}$

C. $\mathrm{S}=\left(\mathrm{a}+\mathrm{b}\right)\times 2\times \mathrm{c}+2\times \mathrm{a}\times \mathrm{b}$

D. $\mathrm{S}=2\left(\mathrm{a}+\mathrm{b}\right)\times \mathrm{a}\times \mathrm{b}$

Câu 4: Tính diện toàn phần của một căn phòng hình hộp chữ nhật có chiều dài 4,5m; chiều rộng 2m, và chiều cao 2,5m.

A. $32,5{\mathrm{m}}^2$

B. $50,5{\mathrm{m}}^2$

C. $55{\mathrm{m}}^2$

D. $45,5{\mathrm{m}}^2$

Câu 5: Một viên gạch dạng hình hộp chữ nhật có chiều dài 22cm, chiều rộng 10cm, chiều cao 5,5cm. Diện tích xung quanh và diện tích toàn phần của viên gạch lần lượt là:

A. $69,5{\mathrm{cm}}^2$ và $509,5{\mathrm{cm}}^2$

B. $68,5{\mathrm{cm}}^2$ và $501,5{\mathrm{cm}}^2$

C. $70,5{\mathrm{cm}}^2$ và $505,5{\mathrm{cm}}^2$

D. $63,5{\mathrm{cm}}^2$ và $520,5{\mathrm{cm}}^2$

Câu 6: Một hộp kem hình hộp chữ nhật có diện tích xung quanh $600{\mathrm{cm}}^2$. Biết chiều cao của hộp kem là 12cm. Tính chu vi đáy của hộp kem đó.

A. $50\mathrm{cm}$

B. $30\mathrm{cm}$

C. $38\mathrm{cm}$

D. $60\mathrm{cm}$

Câu 7: Một hộp đựng ti vi 21 inch. Biết chiều cao của chiếc hộp là 25 inch. Chiều rộng là 23 inch. Chiều dài là 23 inch. Tính diện tích xung quanh của chiếc hộp theo đơn vị inch.

A. $2200{\mathrm{inch}}^2$

B. $2300{\mathrm{inch}}^2$

C. $1200{\mathrm{inch}}^2$

D. $1300{\mathrm{inch}}^2$

Câu 8: Một chiếc hộp làm bằng bìa caton có dạng hình hộp chữ nhật, đáy là hình vuông cạnh 15cm. Chiều cao bằng $\frac{2}{3}$ cạnh đáy. Diện tích bìa làm hộp.

A. $165{\mathrm{cm}}^2$

B. $1050{\mathrm{cm}}^2$

C. $1560{\mathrm{cm}}^2$

D. $1650{\mathrm{cm}}^2$

II. Bài tập tự luận

Câu 1: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có:

a) Chiều dài 18dm, chiều rộng 1,5m và chiều cao 16dm.

b) Chiều dài 3,5m, chiều rộng 1,5m và chiều cao 2m.

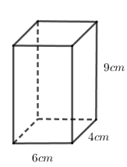
Câu 2: Cho hình vẽ bên, tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật đó.

III. Bài tập vận dụng

Câu 1: Một bể cá không nắp, có chiều dài 3dm, chiều rộng 1,2dm và chiều cao 1,5dm. Tính diện tích toàn phần của bể cá đó.

Câu 2: Một hình hộp chữ nhật có chiều dài gấp ba lần chiều rộng, chiều cao bằng trung bình cộng của ba kích thước. Biết trung bình cộng của chiều dài, chiều rộng và chiều cao là 60. Tính diện tích xung quanh của hình hộp chữ nhật đó. Đơn vị đo bằng cm.

Câu 3: Một khu đất hình chữ nhật có diện tích $2940{\mathrm{m}}^2$ . Người ta xây tường bao quanh để bảo vệ, biết rằng bức tường cao 2m. Tính diện tích tường bao quanh khu đất đó. Biết rằng khu đất có chiều rộng bằng $\frac{3}{5}$ chiều dài.

B. Lý thuyết Diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật

1. Định nghĩa

- Diện tích xung quanh của hình hộp chữ nhật là tổng diện tích bốn mặt bên của hình hộp chữ nhật.

- Diện tích toàn phần của hình hộp chữ nhật là tổng của diện tích xung quanh và diện tích hai đáy.

2. Quy tắc

Giả sử hình hộp chữ nhật có chiều dài là a, chiều rộng là b và chiều cao là h.

- Muốn tính diện tích xung quanh của hình hộp chữ nhật ta lấy chu vi mặt đáy nhân với chiều cao (cùng đơn vị đo).

S_xq = (a + b) × 2 × h

- Muốn tính diện tích toàn phần của hình hộp chữ nhật ta lấy diện tích xung quanh cộng với diện tích hai đáy.

S_tp = S_xq + S_đáy × 2 = (a + b) x 2 x h + 2 x a x b

Lưu ý:

- Chu vi mặt đáy bằng tổng của chiều dài và chiều rộng nhân với 2.

- Diện tích mặt đáy bằng tích của chiều dài và chiều rộng.

3. Một số dạng bài tập

Dạng 1: Tính diện tích xung quanh hoặc diện tích toàn phần của hình hộp chữ nhật

Phương pháp: Áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

Ví dụ: Tính diện tích xung quanh và diện tích toàn phần của hình hộp chữ nhật có chiều dài 8cm, chiều rộng 6cm và chiều cao 4cm.

Bài giải

Chu vi đáy của hình hộp chữ nhật là:

(8 + 6) × 2 = 28 (cm)

Diện tích xung quanh của hình hộp chữ nhật đó là:

28 × 4 = 112 (cm²)

Diện tích một đáy là:

8 × 6 = 48 (cm²)

Diện tích toàn phần của hình hộp chữ nhật đó là:

112 + 48 × 2 = 208(cm²)

Đáp số: Diện tích xung quanh: 112cm²

Diện tích toàn phần: 208cm²

Dạng 2: Biết diện tích xung quanh hoặc diện tích toàn phần, tìm chu vi đáy hoặc chiều cao của hình hộp chữ nhật

Phương pháp:

*) Từ công thức Sxq = (a + b) x 2 x h:

- Tìm chiều cao theo công thức:  h = Sxq : [(a + b) x 2] = S_xq: (a + b) : 2;

- Tìm tổng chu vi đáy theo công thức: (a + b) x 2 = S_xq : h.

*) Nếu biết diện tích toàn phần ta cũng thay vào công thức để tìm các đại lượng chưa biết.

Ví dụ: Cho hình hộp chữ nhật có diện tích xung quanh là 217,5m² và nửa chu vi mặt đáy bằng 14,5m. Tính chiều cao của hình hộp chữ nhật đó.

Bài giải

Chu vi mặt đáy của hình hộp chữ nhật đó là:

14,5 × 2 = 29 (m)

Chiều cao của hình hộp chữ nhật đó là:

217,5 : 29 = 7,5 (m)

Đáp số: 7,5m

Dạng 3: Toán có lời văn (thường là tìm diện tích hộp, căn phòng, sơn tường …)

Phương pháp: Cần xác định xem diện tích cần tìm là diện tích xung quanh hay diện tích toàn phần rồi áp dụng quy tắc tính diện tích xung quanh hoặc diện tích toàn phần.

Ví dụ: Một căn phòng dạng hình hộp chữ nhật có chiều dài 6m, chiều rộng 48dm, chiều cao 4m. Người ta muốn quét vôi các bức tường xung quanh và trần của căn phòng đó. Hỏi diện tích cần quét vôi là bao nhiêu mét vuông, biết tổng diện tích các cửa bằng 12m² (biết rằng chỉ quét vôi bên trong phòng)?

Bài giải

Đổi 48dm = 4,8m

Diện tích xung quanh của căn phòng đó là:

(6 + 4,8) × 2 × 4 = 86,4 (m²)

Diện tích trần của căn phòng đó là:

6 × 4,8 = 28,8 (m²)

Diện tích cần quét vôi là:

86,4 + 28,8 – 12 = 103,2 (m²)

Đáp số: 103,2m²