Tailieumoi.vn xin giới thiệu Bài tập Toán 12 Chương 1 Bài 2: Khối đa diện lồi và khối đa diện đều . Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 12. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 1 Bài 2: Khối đa diện lồi và khối đa diện đều . Mời các bạn đón xem:
Bài tập Toán 12 Chương 1 Bài 2: Khối đa diện lồi và khối đa diện đều
A. Bài tập Khối đa diện lồi và khối đa diện đều
I. Bài tập trắc nghiệm
Câu 1: Khối 20 mặt đều là khối đa diện đều thuộc loại nào?
A. (4; 3)
B. (3; 4)
C. (5; 3)
D. (3; 5)
Khối 20 mặt đều là khối đa diện đều thuộc loại (3; 5)
Câu 2: Khối bát diện đều có bao nhiêu cạnh?
A. 8 cạnh
B. 12 cạnh
C. 24 cạnh
D. 30 cạnh
Khối bát diện đều có 12 cạnh
Câu 3: Khối 12 mặt đều có bao nhiêu cạnh?
A. 12 cạnh
B. 20 cạnh
C. 24 cạnh
D. 30 cạnh
Khối 12 mặt đều có 30 cạnh
Câu 4: Khối 20 mặt đều có bao nhiêu cạnh?
A. 20 cạnh
B. 28 cạnh
C. 30 cạnh
D. 40 cạnh
Khối 20 mặt đều có 30 cạnh
Câu 5: Khối 20 mặt đều có bao nhiêu cạnh?
A. 24 cạnh
B. 28 cạnh
C. 30 cạnh
D. 40 cạnh
Cách 1. Dựa vào lí thuyết (nhận xét c)
Cách 2. Mỗi mặt của nó là tam giác đều nên số cạnh của nó bằng
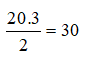
Đáp án là C
Câu 6: Khối 12 mặt đều có bao nhiêu đỉnh ?
A. 10 đỉnh
B. 12 đỉnh
C. 18 đỉnh
D. 20 đỉnh
Cách 1. Dựa vào lí thuyết (nhận xét b)
Cách 2. Khối 12 mặt đều thuộc loại (5 ;3) nên ta có 5.12=3d=2c. Suy ra d=20.
Đáp án là D
Câu 7: Trong các mệnh đề sau, mệnh đề nào sai ?
A. Số mặt của một hình đa diện đều luôn là số chẵn
B. Số đỉnh của một hình đa diện đều luôn là số chẵn
C. Số cạnh của một hình đa diện đều luôn là số chẵn
D. Tồn tại một hình đa diện đều có số cạnh là số lẻ
Cách 1. Dựa vào lí thuyết (nhận xét a, b, c)
Cách 2. Áp dụng công thức pm = 2x , thay m = 4, 8, 12, 20, ta thấy ngay c chẵn. Với hình lập phương ta có 4m = 2c nên c chẵn.
Suy ra D là mệnh đề sai.
Câu 8: Trong các mệnh đề sau, mệnh đề nào sai?
A. Khối lập phương là khối đa diện lồi
B. Khối chóp là khối đa diện lồi
C. Khối lăng trụ là khối đa diện lồi
D. Ghép hai khối đa diện lồi sẽ được một khối đa diện lồi
Hình tạo bởi hai hình chóp có chung một đỉnh duy nhất không phải là khối đa diện lồi. Suy ra D sai.
Câu 9: Trong các mệnh đề sau, mệnh đề nào đúng?
A. Khối đa diện đều loại (p;q) là khối đa diện có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt
B. Khối đa diện đều loại (p;q) là khối đa diện có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều p cạnh
b) Mỗi cạnh của nó là cạnh chung của đúng hai mặt
C. Khối đa diện đều loại (p;q) là khối đa diện có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều p cạnh
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt
D. Khối đa diện đều loại (p;q) là khối đa diện có các tính chất sau:
a) Mỗi mặt của nó là một đa giác đều p cạnh
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt
Dựa vào định nghĩa khối đa diện đều.
Khối đa diện đều loại (p;q) là khối đa diện có các tính chất sau:
* Mỗi mặt của nó là một đa giác đều p cạnh
* Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Câu 10: Khối lập phương là khối đa diện đều thuộc loại nào?
A. (4; 3)
B. (3; 4)
C. (5; 3)
D. (3; 5)
Khối lập phương là khối đa diện đều thuộc loại (4; 3).
II. Bài tập tự luận có lời giải
Câu 1: Khối bát diện là khối đa diện đều thuộc loại nào?
Lời giải:
Khối bát diện là khối đa diện đều thuộc loại (3;4)
Câu 2: Khối 12 mặt đều là khối đa diện đều thuộc loại nào?
Lời giải:
Khối 12 mặt đều là khối đa diện đều thuộc loại (5; 3)
Câu 3: Điền vào chỗ trống cụm từ nào cho dưới đây để được một mệnh đề đúng?
“Tồn tại hình đa diện đều mà các mặt của nó là những….”
Lời giải:
“Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều. Đó chính là khối mười hai mặt đều.
Câu 4: Trong các mệnh đề sau, mệnh đề nào sai?
A. Tồn tại hình đa diện đều mà các mặt của nó là những tam giác đều
B. Tồn tại hình đa diện đều mà các mặt của nó là những hình vuông
C. Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều
D. Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều
Trong các mệnh đề sau, mệnh đề nào sai?
* Tồn tại hình đa diện đều mà các mặt của nó là những tam giác đều. Đó là khối hai mươi mặt đều.
* Tồn tại hình đa diện đều mà các mặt của nó là những hình vuông. Đó là hình lập phương.
* Tồn tại hình đa diện đều mà các mặt của nó là những ngũ giác đều. Đó là khối mười hai mặt đều.
Mệnh đề: Tồn tại hình đa diện đều mà các mặt của nó là những lục giác đều là sai.
Câu 5: Trong các hình đa diện đều sau, hình nào có số đỉnh lớn hơn số mặt?
Lời giải:
Dễ thấy A, B sai. Hình 12 mặt đều thuộc loại (5 ;3) nên 5m = 3d, nên d > m
Câu 6: Trong các hình đa diện đều sau, hình nào có số đỉnh nhỏ hơn số mặt?
Hình tứ diện đều
Hình 12 mặt đều
Hình lập phương
Hình 20 mặt đều
Hình tứ diện đều có 4 đỉnh và 4 mặt
Hình lập phương có 8 đỉnh và 6 mặt
Hình 12 mặt đều có 12 mặt và 20 đỉnh
Hình 20 mặt đều có 20 mặt và 12 đỉnh
Chọn D
Câu 7: Các mặt của khối 12 mặt đều là những đa giác nào?
Lời giải:
Các mặt của khối 12 mặt đều là những ngũ giác đều
Câu 8: Các mặt của khối 20 mặt đều là những đa giác nào?
Lời giải:
Các mặt của khối 20 mặt đều là những tam giác đều
Câu 9: Khối bát diện đều có bao nhiêu đỉnh?
Lời giải:
Khối bát diện đều có 6 đỉnh.
Câu 10: Khối 20 mặt đều có bao nhiêu đỉnh?
Lời giải:
Khối 20 mặt đều thuộc loại (3 ;5), nên ta có 3.20 = 5d, suy ra d = 12
III. Bài tập vận dụng
Bài 1 Có thể chia (H1) thành bao nhiêu khối lập phương bằng (H0) ?
Bài 2 Có thể chia (H2) thành bao nhiêu khối hộp chữ nhật bằng (H1)?
Bài 3 Có thể chia (H) thành bao nhiêu khối hộp chữ nhật bằng (H2) ?
Bài 4 Kim tự tháp Kê-ốp ở Ai Cập (h.1.27) được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự tháp này là một khối chóp tứ giác đều có chiều cao 147 m, cạnh đáy dài 230 m. Hãy tính thể tích của nó.
Bài 5 Tính thể tích khối tứ diện đều cạnh a.
Bài 6 Tính thể tích khối bát diện đều cạnh a.
Bài 7 Cho khối hộp ABCD.A’B’C’D’. Tính tỉ số giữa thể tích của khối hộp đó và thể tích của khối tứ diện ACB’D’.
Bài 8 Cho khối chóp S.ABC. Trên các đoạn thằng SA, SB, SC lần lượt lấy ba điểm A’, B’, C’ khác với S. Chứng minh rằng:
Bài 9 Cho tam giác ABC, vuông cân ở A và AB = a. Trên đường thẳng qua C, vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với BD cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a.
Bài 10 Cho hai đường thẳng chéo nhau d và d’. Đoạn thẳng AB có độ dài bằng a trượt trên d, đoạn thẳng CD có độ dài bằng b trượt trên d’. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi.
B. Lý thuyết Khối đa diện lồi và khối đa diện đều
I. Khối đa diện lồi.
Khối đa diện lồi (H) được gọi là khối đa diện lồi nếu đoạn thẳng nối hai điểm bất kì của (H) luôn thuộc (H). Khi đó đa diện xác định (H) được gọi là đa diện lồi.
Ví dụ 1. Các khối chóp tam giác, tứ giác, các khối lăng trụ tam giác, khối lăng trụ tứ giác… đều là những khối đa diện đều.
- Người ta chứng minh được rằng, một khối đa diện là khối đa diện lồi khi và chỉ khi miềm trong của nó luôn nằm về một phía đối với mỗi mặt phẳng chứa một mặt của nó.
II. Khối đa diện đều.
- Định nghĩa: Khối đa diện đều là khối đa diện lồi có tính chất sau đây:
a) Mỗi mặt của nó là một đa giác đều p cạnh.
b) Mỗi đỉnh của nó là đỉnh chung của đúng q mặt.
Khối đa diện đều như vậy được gọi là khối đa diện đều loại {p; q}.
Từ định nghĩa trên ta thấy các mặt của khối đa diện đều là những đa giác đều bằng nhau.
- Định lí: Chỉ có năm loại khối đa diện đều. Đó là các loại {3; 3}; loại {4; 3}; loại {3; 4}; loại {5; 3} và loại {3; 5}.
Tùy theo số mặt của chúng, năm loại khối đa diện đều kể trên theo thứ tự gọi là các khối tứ diện đều, khối lập phương, khối bát diện đều (hay khối tám mặt đều), khối mười hai mặt đều và khối hai mươi mặt đều.
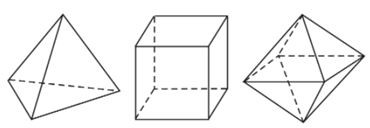
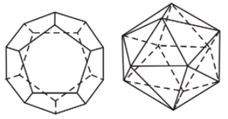
Bảng tóm tắt của năm loại khối đa diện đều.

Ví dụ 2. Chứng minh rằng nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.
Lời giải:
Gọi số cạnh và số mặt của đa diện lần lượt là c và m .
Vì mỗi mặt có ba cạnh và mỗi cạnh là cạnh chung của đúng hai mặt nên ta có số cạnh của đa diện là .
Do đó, 3m chia hết cho 2 mà 3 không chia hết cho 2 nên m phải chia hết cho 2, nghĩa là m là số chẵn.
Vậy nếu khối đa diện có các mặt là những tam giác thì tổng các mặt của nó phải là một số chẵn.