Tailieumoi.vn xin giới thiệu Bài tập Toán 8 Chương 4 Bài 7: Hình chóp đều và hình chóp cụt đều. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 8. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Chương 4 Bài 7: Hình chóp đều và hình chóp cụt đều. Mời các bạn đón xem:
Bài tập Toán 8 Chương 4 Bài 7: Hình chóp đều và hình chóp cụt đều
A. Bài tập Hình chóp đều và hình chóp cụt đều
I. Bài tập trắc nghiệm
Bài 1: Chọn phát biểu sai trong các phát biểu sau?
A. Hình chóp đều là hình chóp có đáy là một đa giác bất kì, các mặt bên là những tam giác bất kì có chung đỉnh.
B. Chân đường cao của hình chóp đều trùng với tâm của đường tròn đi qua các đỉnh của mặt đáy.
C. Đường cao vẽ từ đỉnh của mỗi mặt bên của hình chóp đều được gọi là trung đoạn của hình chóp đó.
D. Trong hình chóp đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy gọi là đường cao.
Áp dụng định nghĩa của hình chóp: Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là những tam giác cân bằng nhau có chung đỉnh.
Phát biểu A sai.
Chọn đáp án A.
Bài 2: Mặt bên của hình chóp cụt đều là hình gì?
A. Hình chữ nhật
B. Hình vuông.
C. Hình thang cân
D. Tứ giác bất kì
Áp dụng định nghĩa của hình thang cân ta có: Mỗi mặt bên của hình chóp cụt đều là một hình thang cân.
Chọn đáp án C.
Bài 3: Hình chóp tứ giác đều có mặt bên là hình gì?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Tam giác vuông cân
Hình chóp tứ giác đều có mặt bên là tam giác cân.
Chọn đáp án A.
Bài 4: Hình chóp lục giác đều có bao nhiêu mặt?
A. 4
B. 5
C. 6
D. 7
Hình chóp lục giác đều gồm có 6 mặt bên và 1 mặt đáy.
Chọn đáp án D.
Bài 5: Hình chóp tam giác đều có đáy là?
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Hình vuông
Hình chóp tam giác đều có đáy là tam giác đều.
Chọn đáp án B
Bài 6: Hình chóp ngũ giác đều có bao nhiêu mặt bên?
A. 5
B. 6
C. 4
D. 7
Hình chóp ngũ giác đều có đáy là ngũ giác đều và có 5 mặt bên.
Chọn đáp án A
Bài 7: Hình chóp tứ giác đều có tất cả bao nhiêu mặt?
A. 3
B. 4
C. 5
D. 6
Hình chóp tứ giác đều có 4 mặt bên và 1 mặt đáy
Vậy có tất cả 5 mặt
Chọn đáp án C
Bài 8: Hình chóp lục giác đều có bao nhiêu cạnh ?
A. 6
B.7
C. 10
D.12
Hình chóp lục giác đều có đáy là lục giác đều có 6 cạnh bằng nhau và có 6 cạnh bên.
Do đó, có tất cả 6 + 6 = 12 cạnh
Chọn đáp án D
Bài 9: Cho hình chóp tứ giác đều. Khi đó:
A. Đáy là hình vuông
B. Có 4 mặt bên
C. Có tất cả 8 cạnh
D. Số mặt của hình chóp là 4.
Chọn khẳng định sai
Hình chóp tứ giác đều có:
+ Đáy là hình vuông.
+ Có 4 mặt bên và 1 mặt đáy. Nên có tất cả 5 mặt.
+ Số cạnh đáy là 4, số cạnh bên là 4 nên có tất cả 8 cạnh
Chọn đáp án D
II. Bài tập tự luận có giải
Bài 1 Tính diện tích xung quanh của hình chóp cụt tứ giác đều có các cạnh đáy bằng 6cm và 8cm, chiều cao của mặt bên bằng 5cm.
Lời giải
Mặt bên hình chóp cụt tứ giác đều là hình thang cân nên diện tích một mặt bên bằng: 
Hình chóp cụt tứ giác đều có 4 mặt bên bằng nhau nên diện tích xung quanh bằng 35.4 = 140 (cm2)
Bài 2: Cắt từ tấm bìa cứng thành các hình như ở hình 118 rồi gấp lại để có những hình chóp đều.
Lời giải
Bài 3 Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
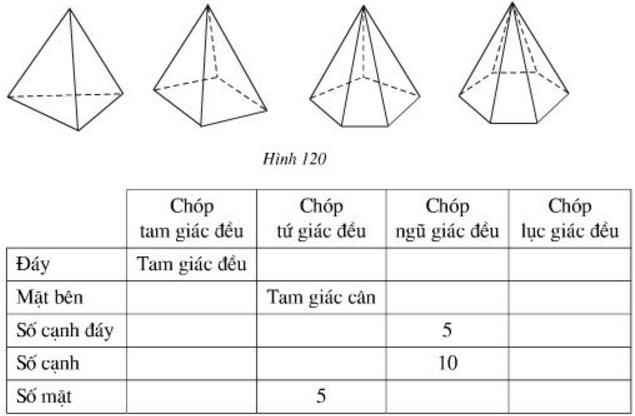
Lời giải:
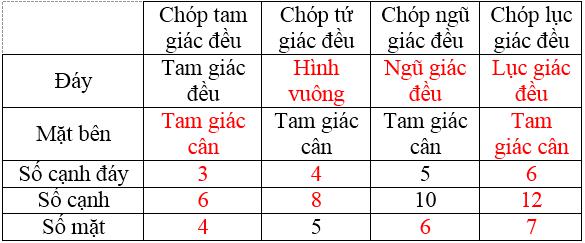
Bài 4 Hãy xét sự đúng sai của các phát biểu sau:
a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
Lời giải:
a) Sai, vì hình thoi không phải là tứ giác đều (các góc không bằng nhau).
b) Sai, vì hình chữ nhật không phải là tứ giác đều (các cạnh không bằng nhau).
Bài 5 Trong các tấm bìa ở hình 121, em gấp lại tấm bìa nào thì có được một hình chóp đều?
Hình 121
Lời giải:
Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.
Bài 6 Thực hành: Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 để có thể ghép được các mặt bên của một hình chóp tứ giác đều (h.122).
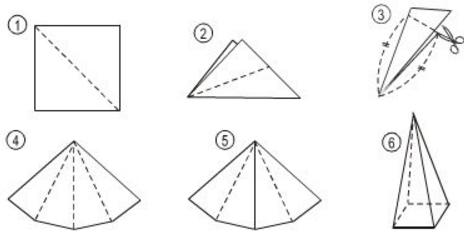
Hình 122
Lời giải:
Các bạn tự thực hành ở nhà để giúp mình dễ tưởng tượng hình chóp đều hơn.
III. Bài tập vận dụng
Bài 1 Quan sát hình 120 và điền cụm từ và số thích hợp vào các ô trống ở bảng sau, biết rằng các hình đã cho là những hình chóp đều.
Bài 2 Hãy xét sự đúng sai của các phát biểu sau:
a) Hình chóp đều có đáy là hình thoi và chân đường cao trùng với giao điểm hai đường chéo của đáy.
b) Hình chóp đều có đáy là hình chữ nhật và chân đường cao trùng với giao điểm hai đường chéo của đáy.
Trong các tấm bìa ở hình 121, em gấp lại tấm bìa nào thì có được một hình chóp đều?
Bài 3 Thực hành: Từ tờ giấy cắt ra một hình vuông rồi thực hiện các thao tác theo thứ tự từ 1 đến 6 để có thể ghép được các mặt bên của một hình chóp tứ giác đều (h.122).
B. Lý thuyết Hình chóp đều và hình chóp cụt đều
1.Hình chóp
|
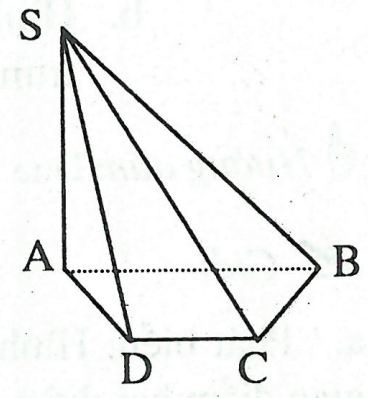
Định nghĩa: Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là các tam giác có chung đỉnh. Hình bên cho ta hình ảnh của hình chóp S.ABCD, và ở đó: 1. Điểm S được gọi là đỉnh của hình chóp. 2. Các đoạn SA, SB, SC, SD được gọi là các cạnh bên của hình chóp. 3. Các tam giác SAB, SBC, SCD, SAD được gọi là các mặt bên của hình chóp. |
4. Mặt ABCD là đáy của hình chóp.
5. Hình chóp này có đáy là tứ giác nên gọi là hình chóp tứ giác.
2. Hình chóp đều
Định nghĩa: Hình chóp đều là hình chóp có đáy là một đa giác đều, các mặt bên là tam giác cân bằng nhau có chung đỉnh.
|
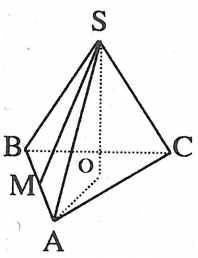
Hình bên cho ta hình ảnh của hình chóp tam giác đều S.ABC, và ở đó: 1. Điểm S được gọi là đỉnh của hình chóp. 2. Các đoạn SA, SB, SC bằng nhau được gọi là các cạnh bên của bên hình chóp. 3. Các tam giác SAB, SBC, SAC là các tam giác cân đỉnh S, chúng được gọi là các mặt bên của hình chóp. 4. ABC là một tam giác đều và nó được gọi là đáy của hình chóp. |
5. Đoạn SM (với M là trung điểm của AB) được gọi là trung đoạn.
6. Đoạn SO (với O là tâm của đáy ABC) được gọi là đường cao.
7. Hình chóp này có đáy là tam giác đều nên gọi là hình chóp tam giác đều.
3. Hình chóp cụt đều
|
Định nghĩa: Cắt một hình chóp đều bằng một mặt phẳng song song với đáy, phần hình chóp nằm giữa mặt phẳng đó và mặt phẳng đáy là một hình chóp cụt đều. Hình bên cho ta hình ảnh của hình chóp cụt đều và ở đó mỗi mặt bên của nó đều là những hình thang cân bằng nhau. |
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
