Tailieumoi.vn xin giới thiệu bộ đề thi học kì 1 môn Toán lớp 10 sách Cánh diều năm 2025 – 2026. Tài liệu gồm 4 đề thi có ma trận chuẩn bám sát chương trình học và đáp án chi tiết, được biên soạn bởi đội ngũ giáo viên THPT dày dặn kinh nghiệm sẽ giúp các em ôn tập kiến thức và rèn luyện kĩ năng nhằm đạt điểm cao trong bài thi học kì 1 Toán 10. Mời các bạn cùng đón xem:
Chỉ từ 150k mua trọn bộ Đề thi học kì 1 Toán 10 Cánh diều bản word có lời giải chi tiết (chỉ 20k cho 1 đề thi bất kì):
B1: Gửi phí vào tài khoản 0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây
Xem thử tài liệu tại đây: Link tài liệu
Đề thi học kì 1 Toán lớp 10 Cánh diều có đáp án - Đề 1
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
Năm học ...............
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 1)
Phần I: Trắc nghiệm (6 điểm).
Câu 1: Cho đồ thị hàm số như hình bên:
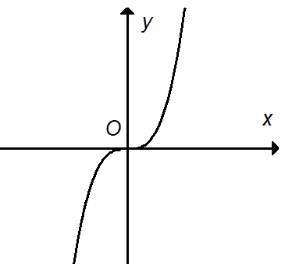
Khẳng định nào sau đây sai?
A. Hàm số đồng biến trên khoảng .
B. Hàm số đồng biến trên khoảng .
C. Hàm số đồng biến trên khoảng .
D. Hàm số đồng biến tại gốc tọa độ O.
Câu 2: Hàm số xác định khi nào?
A. . B. . C. . D. .
Câu 3: Đồ thị hàm số nhận đường thẳng nào dưới đây làm trục đối xứng?
A. B. C. D.
Câu 4: Hàm số đồng biến trên khoảng:
A. B.
C. D.
Câu 5: Cho và một điểm , có bao nhiêu điểm thỏa mãn
A. B. C. D. Vô số.
Câu 6: Cho lục giác đều ABCDEF tâm . Số các vectơ khác vectơ không, cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác là:
A. B. C. D. .
Câu 7: Cho ba điểm phân biệt. Đẳng thức nào sau đây sai?
A. B. C. D.
Câu 8: Cho đoạn thẳng MN lấy điểm sao cho . Điểm được xác định bởi hình vẽ nào sau đây?
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
Câu 9: Cho hai vector thỏa . Tính tích vô hướng .
A. . B. . C. . D. .
Câu 10: Cho hàm số . Tính .
A. B. C. D.
Câu 11: Bảng biến thiên sau là của hàm số nào?
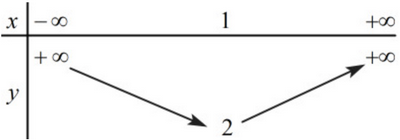
A. B. C. D.
Câu 12: Đường thẳng cắt parabol tại hai điểm có hoành độ lần lượt là
A. . B. . C. . D. .
Câu 13: Một vật được ném lên trên cao và độ cao của nó so với mặt đất được cho bởi công thức , với là thời gian tính bằng giây kể từ lúc bắt đầu ném. Độ cao cực đại mà vật đó có thể đạt được so với mặt đất bằng bao nhiêu mét?
A. B. C. 15 D. 16
Câu 14: Cho . Xác định để với mọi .
A. B. C. D. và .
Câu 15: Trong các tập hợp sau đây, tập nào có chứa phần tử không phải là nghiệm của bất phương trình ?
A. B. C. D.
Câu 16: Giải phương trình sau
A. B. C. D.
Câu 17: Cho hình thoi ABCD tâm , cạnh bằng , và góc bằng . Kết luận nào đúng?
A. B. C. D.
Câu 18: Cho tam giác ABC.Tập hợp các điểm thỏa mãnlà?
A. đường thẳng AB.
B. trung trực đoạn BC.
C. đường tròn tâm A, bán kính BC.
D. đường thẳng qua và song song vơi BC.
Câu 19: Cho tam giác ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM. Trong các mệnh đề sau, mệnh đề nào đúng?
A. B.
C. D.
Câu 20: Cho đoạn thẳng AB và là một điểm nằm trên đoạn AB sao cho . Giá trị của để có đẳng thức là:
A. B. C. D.
Câu 21: Cho hai vectơ và khác . Xác định góc giữa hai vectơ và biết .
A. . B. . C. . D. .
Câu 22: Tìm tất cả các giá trị thực của tham số để hàm số xác định trên .
A. B. C. D.
Câu 23: Parabol đi qua A(0;-1), B(1;-1), C(-1;1) có phương trình là:
A. B. C. D.
Câu 24: Giá trị dương lớn nhất để hàm số xác định là
A. B. C. D.
Câu 25: Cho tam giác ABC nhọn, có H là trực tâm. nội tiếp . Gọi M là trung điểm BC. Khẳng định nào sau đây là đúng
A. cùng hướng. B. cùng hướng.
C. cùng hướng. D. Cả A, B, C đều sai.
Câu 26: Cho hình bình hành ABCD, . Khẳng định nào sau đây đúng?
A. cùng hướng với B. cùng hướng với
C. ngược hướng với D. ngược hướng với
Câu 27: Cho tam giác ABC, có sao cho . Hãy phân tích theo hai vectơ .
A. B.
C. D.
Câu 28: Cho hình bình hành ABCD có , , góc nhọn và diện tích tam giác ABC bằng Khi đó bằng
A. B.
C. D.
Câu 29: Cho tam giác ABC đều, cạnh bằng , điểm thuộc đường tròn ngoại tiếp tam giác ABC và thỏa mãn . Bán kính đường tròn đó là
A. B.
C. D.
Câu 30: Cho hàm số biết hàm số đạt giá trị lớn nhất trên bằng 4 khi và tổng bình phương các nghiệm của phương trình bằng 10. Hàm số đã cho là hàm số nào sau đây?
A. . B. . C. . D. .
Phần II: Tự luận (4 điểm)
Câu 1: Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó là thời gian kể từ khi quả bóng được đá lên; là độ cao của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao theo thời gian và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
Câu 2: Cho hình bình hành ABCD và hai điểm được xác định bởi các hệ thức sau: ,
a) Chứng minh A, E, F thẳng hàng.
b) M là điểm thỏa mãn . Chứng minh là trung điểm CD
Câu 3: Cho hàm số với a, b, c là các hệ số, . Biết rằng đồng biến trên khoảng , hãy tìm giá trị lớn nhất của biểu thức .
Hướng dẫn giải:
I. Phần trắc nghiệm
|
1.D |
2.D |
3.C |
4.D |
5.A |
6.B |
7.D |
8.B |
9.A |
10.C |
|
11.C |
12.D |
13.A |
14.A |
15.D |
16.B |
17.A |
18.C |
19.C |
20.B |
|
21.D |
22.A |
23.B |
24.A |
25.B |
26.B |
27.B |
28.A |
29.C |
30.D |
Câu 1 (NB):
Phương pháp:
Quan sát đồ thị, xác định khoảng đồng biến là khoảng ứng với đồ thị đi lên, khoảng nghịch biến là khoảng ứng với đồ thị đi xuống.
Cách giải:
Dựa vào đồ thị hàm số ta thấy hàm số đồng biến trên khoảng nên các đáp án A, B, C đúng.
Chọn D.
Câu 2 (NB):
Phương pháp:
Ta có: xác định khi và chỉ khi .
Cách giải:
Hàm số xác định khi và chỉ khi .
Chọn D.
Câu 3 (NB):
Phương pháp:
Đồ thị hàm số có trục đối xứng .
Cách giải:
Hàm số có các hệ số a = 3, b = 4, c = – 1.
Vậy đồ thị hàm số có trục đối xứng .
Chọn C.
Câu 4 (NB):
Phương pháp:
Hàm số đồng biến trên khoảng .
Cách giải:
Hàm số đồng biến trên khoảng .
Chọn D.
Câu 5 (NB):
Phương pháp:
Sử dụng định nghĩa hai vecto bằng nhau.
Cách giải:
Mà cùng hướng
Nên có duy nhất một điểm D để
Chọn A.
Câu 6 (NB):
Phương pháp:
ABCDEF là lục giác đều nên DE, AB, CO song song với nhau.
Sử dụng định nghĩa hai vecto cùng phương.
Cách giải:
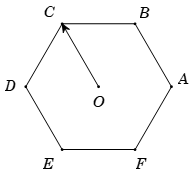
Các vectơ khác vectơ không, cùng phương với có điểm đầu và điểm cuối là các đỉnh của lục giác là: .
Chọn B.
Câu 7 (NB):
Phương pháp:
Quy tắc cộng, trừ vectơ cơ bản.
Cách giải:
là đẳng thức sai.
Chọn D.
Câu 8 (NB):
Phương pháp:
Áp dụng tính chất của phép nhân vecto với một số.
Cách giải:
Ta có: là hai vecto ngược chiều hay nằm giữa và
Trong các đáp án, chỉ có đáp án B đúng.
Chọn B.
Câu 9 (NB):
Phương pháp:
Cách giải:
Ta có: .
Chọn A.
Câu 10 (TH):
Phương pháp:
Tính giá trị hàm số tại 1 điểm.
Cách giải:
Vậy .
Chọn C.
Câu 11 (TH):
Phương pháp:
Dựa vào BBT nhận xét đỉnh của đồ thị hàm số và tọa độ đỉnh của đồ thị hàm số.
Cách giải:
Đồ thị hàm số có bề lõm hướng lên nên a > 0 => Loại đáp án D.
Đồ thị hàm số có đỉnh I(1;2) nên loại A và B.
Chọn C.
Câu 12 (TH):
Phương pháp:
Hoành độ giao điểm của hai đồ thị hàm số là nghiệm của phương trình hoành độ giao điểm của hai đồ thị hàm số.
Cách giải:
Xét phương trình hoành độ giao điểm của và :
Chọn D.
Câu 13 (TH):
Phương pháp:
Hàm số bậc hai với đạt GTLN tại .
Cách giải:
Ta có có đồ thị là parabol có bề lõm hướng xuống, đạt GTLN tại .
Vậy .
Chọn A.
Câu 14 (TH):
Phương pháp:
Xét hai trường hợp: và .
Trong trường hợp , là tam thức bậc hai, tìm để với mọi .
Cách giải:
TH1. . Khi đó: .
Suy ra không thỏa yêu cầu bài toán.
TH2.
(thoả mãn điều kiện).
Chọn A.
Câu 15 (TH):
Phương pháp:
Tìm các nghiệm của biểu thức , lập bảng xét dấu và kết luận.
Áp dụng định nghĩa: Tập hợp là tập hợp con của tập hợp nếu tất cả các phần tử của đều nằm trong .
Cách giải:
Giải:
Bảng xét dấu:

Tập nghiệm của bất phương trình là .
Vì là tập có chứa phần tử không phải là nghiệm của bất phương trình.
Chọn D.
Câu 16 (TH):
Phương pháp:
Giải phương trình
Cách giải:
Vậy phương trình đã cho có nghiệm duy nhất
Chọn B.
Câu 17 (TH):
Phương pháp:
Tam giác ABD là tam giác đều cạnh a.
Tính độ dài OA.
Cách giải:
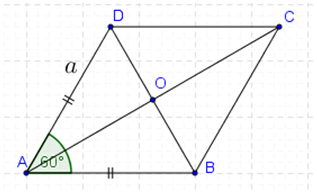
Ta có tam giác ABD là tam giác đều cạnh nên .
Chọn A.
Câu 18 (TH):
Phương pháp:
Tìm các vectơ hiệu , .
Suy ra hai đoạn thẳng bằng nhau và xác định vị trí M.
Cách giải:
Ta có
Mà cố định Tập hợp điểm là đường tròn tâm , bán kính BC.
Chọn C.
Câu 19 (TH):
Phương pháp:
Sử dụng các đẳng thức vectơ liên quan đến trung điểm:
- Nếu I là trung điểm của AB thì .
- Với mọi điểm M, I là trung điểm của AB thì .
Cách giải:
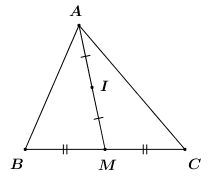
Vì I là trung điểm của AM nên .
Mà M là trung điểm của BC nên .
Do đó hay .
Chọn C.
Câu 20 (TH):
Phương pháp:
Áp dụng định nghĩa tích của một vecto với một số.
Cách giải:

Ta có:
Theo đề bài, ta có:
Mà và cùng hướng nên .
Chọn B.
Câu 21 (TH):
Phương pháp:
Sử dụng công thức .
Cách giải:
Ta có: .
Vậy góc giữa hai vectơ và là .
Chọn D.
Câu 22 (VD):
Phương pháp:
Hàm số xác định
Cách giải:
Hàm số xác định trên
Chú ý khi giải:
Các em có thể làm theo cách 2:
Hàm số xác định trên
Chọn A.
Câu 23 (VD):
Phương pháp:
Thay tọa độ các điểm A, B, C vào hàm số, lập hệ phương trình và giải tìm a, b, c.
Cách giải:
Vì A, B, C thuộc đồ thị hàm số nên ta có hệ phương trình .
Vậy .
Chọn B.
Câu 24 (VD):
Phương pháp:
Hàm số xác định .
Cách giải:
Hàm số xác định khi và chỉ khi .
Giải .
Ta có bảng xét dấu:

Dựa vào bảng xét dấu, ta thấy .
Vậy giá trị dương lớn nhất để hàm số xác định là .
Chọn A.
Câu 25 (VD):
Phương pháp:
- Vẽ hình.
- Từ M là trung điểm BC. Xác định tính đúng sai của A và C.
- Chứng minh Suy ra cùng hướng.
Cách giải:
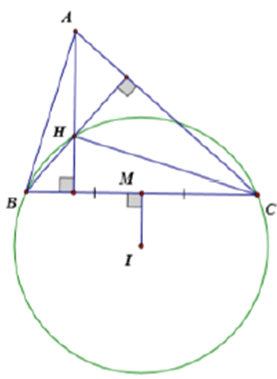
Vì suy ra
Mà H là trực tâm của tam giác ABC nên .
Suy ra
Từ đó, cùng hướng.
Chọn B.
Câu 26 (VD):
Phương pháp:
Cách 1: Gọi , biểu diễn vectơ qua điểm O, và xác định hướng của .
Cách 2: Sử dụng quy tắc hình bình hành, biểu diễn , , thay vào vectơ .
Cách giải:
Cách1:
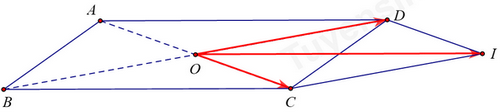
Gọi . Khi đó:
(Với là điểm thỏa mãn tứ giác ODIC là hình bình hành như hình vẽ). Khi đó ta có cùng hướng với .
Cách 2:
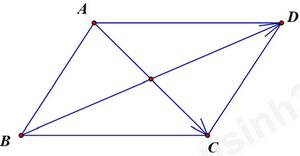
Ta có: .
Vậy cùng hướng với .
Chọn B.
Câu 27 (VD):
Phương pháp:
Sử dụng phương pháp phân tích một vecto theo hai vecto không cùng phương.
Cách giải:
Theo đề bài, ta có hình vẽ:
Mà .
Chọn B.
Câu 28 (VD):
Phương pháp:
Áp dụng công thức diện tích tam giác
Và tính
Cách giải:
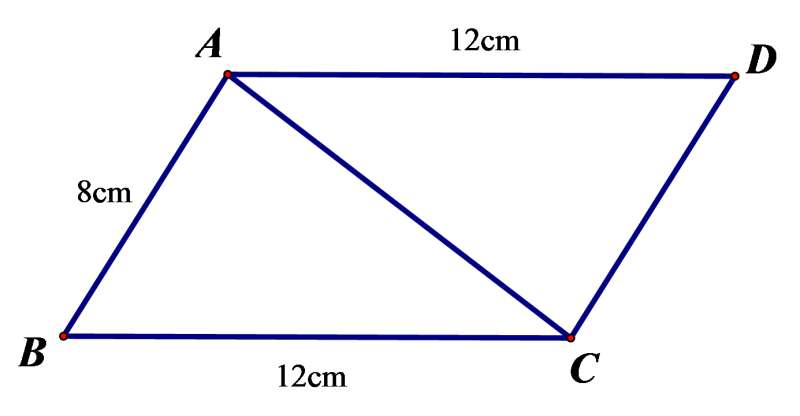
( vì nhọn )
Chọn A.
Câu 29 (VDC):
Phương pháp:
Áp dụng: Trong tam giác đều, tâm đường tròn ngoại tiếp tam giác cũng là trọng tâm của tam giác đó.
Cách giải:
Gọi là trọng tâm tam giác ABC, ta có: ,
và
Vì đều nên cũng là tâm đường tròn ngoại tiếp tam giác ABC.
Ta có:
Mà suy ra .
Suy ra, điểm nằm trên đường tròn tâm bán kính .
Chọn C.
Câu 30 (VDC):
Phương pháp:
Vì hàm số đạt giá trị lớn nhất trên bằng 4 khi nên ta có đỉnh được hệ 2 phương trình 3 ẩn
Sử dụng giả thiết tổng bình phương các nghiệm của phương trình bằng 10 tức .
Áp dụng định lý Vi-et được phương trình thứ 3 ẩn
Ta giải hệ 3 phương trình 3 ẩn được cần tìm.
Cách giải:
Hàm số là hàm số bậc 2 nên có đỉnh
Vì hàm số đạt giá trị lớn nhất trên bằng 4 khi nên đồ thị hàm số có đỉnh và
Xét phương trình: có hai nghiệm
Áp dụng định lý Vi-et ta có:
Theo đề bài ta có:
Chọn D.
Phần II: Tự luận
Câu 1 (VD):
Phương pháp:
Chọn hệ trục toạ độ.
Giả sửa (P) có phương trình
Các điểm A, B, C tương ứng tại các thời điểm t là 0; 1; 2 thuộc (P) nên ta có các phương trình theo ẩn a, b, c.
Giải hệ phương trình ẩn a, b, c ta tìm được Parabol.
Cách giải:
Tại
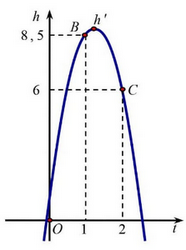
Chọn hệ trục Oth như hình, (P) có phương trình .
Giả sử tại thời điểm t'thì quả bóng đạt độ cao lớn nhất h'.
Theo đề bài ta có:
tại nên
tại nên
tại nên
Thay toạ độ 3 điểm A, B, C vào (P) ta có:
Vậy hàm số bậc hai cần tìm có dạng:
Câu 2 (TH):
Phương pháp:
a) Từ hệ thức đề bài cho, xác định vị trí điểm E, F.
Tách biểu thức rồi biến đổi đưa về dạng . Từ đó suy ra A, E, F thẳng hàng.
b) Chứng minh M là trung điểm AE.
Chứng minh ACED là hình hình hành.
Suy ra M là trung điểm CD.
Cách giải:
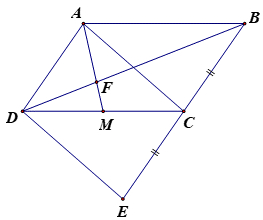
a) Ta có
, suy ra là trung điểm EB.
sao cho .
.
Mặt khác
Vậy thẳng hàng.
b) là trung điểm .
Mặt khác là hình bình hành (vì ) nên cũng là trung điểm của .
Câu 3 (VDC):
Phương pháp:
Từ và đồng biến trên khoảng xác định bất đẳng thức của .
Chia cả tử và mẫu của P cho null đưa về ẩn và tìm GTLN.
Cách giải:
Do nên đồng biến trên .
Từ đây ta có: đồng biến trên .
Ta có , với .
Có , . Dấu bằng xảy ra khi .
Do đó , đạt được khi .
Đề thi học kì 1 Toán lớp 10 Cánh diều có đáp án - Đề 2
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
Năm học ...............
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 2)
MA TRẬN ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 90 phút
|
TT |
Nội dung kiến |
Đơn vị kiến thức |
Mức độ nhận thức |
Tổng |
% |
|||||||||
|
Nhận biết |
Thông hiểu |
Vận dụng |
Vận dụng cao |
Số CH |
Thời |
|||||||||
|
Số |
Thời |
Số |
Thời |
Số |
Thời gian (phút) |
Số |
Thời |
TN |
TL |
|||||
|
1 |
1. Mệnh đề. Tập hợp |
1.1. Mệnh đề |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
7,5 |
9,3 |
|
1.2. Tập hợp. Các phép toán trên tập hợp |
1 |
1,5 |
|
|
1 |
3 |
|
|
2 |
0 |
||||
|
2 |
2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
Bất phương trình, hệ bất phương trình bậc nhất hai ẩn và ứng dụng |
2 |
3 |
1 |
2 |
|
|
|
|
3 |
0 |
5 |
7 |
|
3 |
3. Hàm số bậc |
3.1. Hàm số và đồ thị |
2 |
3 |
1 |
2 |
|
|
|
|
3 |
0 |
46 |
43,3 |
|
3.2. Hàm số bậc hai |
1 |
1 |
|
|
1 |
6 |
|
|
2 |
0 |
||||
|
3.3. Dấu tam thức bậc hai |
|
|
1 |
2 |
|
|
|
|
1 |
0 |
||||
|
3.4. Bất phương trình bậc hai |
1 |
1 |
1 |
2 |
|
|
1 |
15 |
2 |
1 |
||||
|
3.5. Hai phương trình bậc hai |
|
|
1 |
2 |
2 |
12 |
|
|
2 |
1 |
||||
|
4 |
4. Hệ thức lượng trong tam giác |
4.1. Giá trị lượng giác của một góc từ 0° đến 180°. Định lí sin và định lí côsin |
1 |
1,5 |
2 |
4 |
|
|
|
|
3 |
0 |
8,5 |
11,7 |
|
4.1. Giải tam giác. Diện tích tam giác |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
||||
|
5 |
5. Vectơ |
5.1. Khái niệm vectơ |
2 |
2 |
|
|
|
|
|
|
2 |
0 |
23 |
28,7 |
|
5.2. Tổng và hiệu của hai vectơ |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
||||
|
5.3. Tích của vectơ với một số |
1 |
1 |
1 |
2 |
1 |
12 |
|
|
2 |
1 |
||||
|
5.4. Tích vô hướng của 2 vectơ |
1 |
1 |
1 |
2 |
|
|
|
|
2 |
0 |
||||
|
Tổng |
|
15 |
18 |
12 |
24 |
5 |
33 |
1 |
15 |
30 |
3 |
90 |
100 |
|
|
Tỉ lệ (%) |
|
35 |
28 |
17 |
20 |
70 |
30 |
|
100 |
|||||
|
Tỉ lệ chung (%) |
|
63 |
37 |
|
|
|
100 |
|||||||
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 90 phút
|
TT |
Nội dung |
Đơn vị |
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá |
Số câu hỏi theo mức độ nhận thức |
|||
|
Nhận |
Thông |
Vận |
Vận dụng |
||||
|
1 |
1. Mệnh |
1.1. Mệnh đề |
Nhận biết: – Nhận biết được thế nào là mệnh đề toán học, tính đúng/sai của các mệnh đề toán học trong trường hợp đơn giản. |
1 |
1 |
|
|
|
1.2. Tập hợp. Các phép toán trên tập hợp |
Thông hiểu – Thực hiện được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể. |
1 |
|
1 |
|
||
|
2 |
2. Bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
Bất phương trình, hệ bất phương trình bậc nhất hai ẩn và ứng dụng |
Nhận biết: – Nhận biết được bất phương trình và hệ bất phương trình bậc nhất hai ẩn |
2 |
1 |
|
|
|
3 |
3. Hàm số bậc hai và đồ thị |
3.1. Hàm số và đồ thị |
Nhận biết: – Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái niệm hàm số. Thông hiểu: – Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số. – Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. |
2 |
1 |
|
|
|
3.2. Hàm số bậc hai |
Nhận biết: – Nhận biết được các tính chất cơ bản của Parabol như đỉnh, trục đối xứng. Thông hiểu: – Tính được bảng giá trị của hàm số bậc hai. – Vẽ được Parabol (parabol) là đồ thị hàm số bậc hai. – Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị. Vận dụng: – Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn. (ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabol, ...). Vận dụng cao: - Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết các bài toán chứa tham số. |
1 |
|
1 |
|
||
|
|
|
3.3. Dấu tam thức bậc hai |
Thông hiểu: - Giải thích được định lí về dấu của tam thức bậc hai từ việc quan sát đồ thị của hàm số bậc hai. - Giải được bất phương trình bậc hai. Vận dụng: - Vận dụng được bất phương trình bậc hai một ẩn vào giải quyết bài toán thực tiến (ví dụ: xác định chiều cao tối đa để xe có thể qua hầm có hình dạng parabol, ...).
|
|
1 |
|
|
|
|
|
3.4. Bất phương trình bậc hai |
1 |
1 |
|
1 |
|
|
|
|
3.5. Phương trình quy về phương trình bậc hai |
Thông hiểu: - Tìm được điều kiện xác định của phương trình chứa căn thức và giải được một số phương trình chứa căn đơn giản. Vận dụng: - Giải được phương trình chứa căn thức có dạng: ; . |
|
1 |
2 |
|
|
4 |
4. Hệ thức lượng trong tam giác |
4.1. Giá trị lượng giác của một góc từ 0° đến 180° |
Nhận biết: – Nhận biết được giá trị lượng giác của một góc từ 0° đến 180°. – Nhận biết được hệ thức liên hệ giữa giá trị lượng giác của các góc phụ nhau, bù nhau. Thông hiểu: – Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay. |
1 |
1 |
|
|
|
4.2. Định lí côsin và định lí sin |
Thông hiểu: – Tính được giá trị lượng giác (đúng hoặc gần đúng) của một góc từ 0° đến 180° bằng máy tính cầm tay. – Giải thích được các hệ thức lượng cơ bản trong tam giác: định lí côsin, định lí sin, công thức tính diện tích tam giác. |
|
1 |
|
|
||
|
4.3. Giải tam giác và ứng dụng thực tế |
Vận dụng: – Mô tả được cách giải tam giác và vận dụng được vào việc giải một số bài toán có nội dung thực tiễn (ví dụ: xác định khoảng cách giữa hai địa điểm khi gặp vật cản, xác định chiều cao của vật khi không thể đo trực tiếp,...). |
1 |
1 |
|
|
||
|
5 |
5. Vectơ |
5.1. Khái niệm vectơ |
Nhận biết: – Nhận biết được khái niệm vectơ, vectơ bằng nhau, vectơ-không. Thông hiểu: – Mô tả được một số đại lượng trong thực tiễn bằng vectơ. – Thực hiện được các phép toán trên vectơ (tổng và hiệu hai vectơ, tích của một số với vectơ, tích vô hướng của hai vectơ) và mô tả được những tính chất hình học (ba điểm thẳng hàng, trung điểm của đoạn thẳng, trọng tâm của tam giác,...) bằng vectơ. Vận dụng: – Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên quan đến Vật lí và Hoá học (ví dụ: những vấn đề liên quan đến lực, đến chuyển động,...). – Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán liên quan đến thực tiễn (ví dụ: xác định lực tác dụng lên vật,...) Vận dụng cao: - Tìm tập hợp các điểm thỏa mãn một đẳng thức vectơ. |
2 |
|
|
|
|
5.2. Tổng và hiệu của hai vectơ |
1 |
1 |
|
|
|||
|
5.3. Tích của vectơ với một số |
1 |
1 |
1 |
|
|||
|
5.4. Tích vô hướng của 2 vectơ |
1 |
1 |
|
|
|||
|
6.2. Mô tả bằng bảng dữ liệu |
2 |
|
|
|
|||
|
6.3. Các số đặc trưng đo xu thế trung tâm |
1 |
1 |
|
|
|||
|
6.4. Các số đặc trưng đo độ phân tán |
|
1 |
1 |
|
|||
|
Tổng |
|
15 |
12 |
5 |
1 |
||
A. TRẮC NGHIỆM (5,0 điểm)
Câu 1. Trục đối xứng của parabol y = x2 + 3x – 1 là đường thẳng:
A. ;
B. ;
C. ;
D. .
Câu 2. Cho α là góc nhọn. Khẳng định nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
Câu 3. Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?
Câu 4. Cho tam giác ABC vuông tại A, AB = 2, . Độ dài của vectơ gần với giá trị nào nhất sau đây:
A. 2,1;
B. 6,5;
C. 2,5;
D. 6,0.
Câu 5. Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là:
A. ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0;
B. ∀x ∈ ℝ, x3 – 2x + 1 < 0”;
C. ∃x ∈ ℝ, x3 – 2x + 1 ≥ 0”;
D. ∀x ∈ ℝ, x3 – 2x + 1 > 0”.
Câu 6. Cho hai vectơ đều khác vectơ > Tích vô hướng của và được xác định bởi công thức
Câu 7. Cho hình bình hành ABCD, có M là trung điểm của BC, G là trọng tâm của tam giác ABC (tham khảo hình vẽ bên). Khi đó . Vậy k bằng:
A. ;
B. ;
C. ;
D. k = 3.
Câu 8. Cho hai tập hợp A = {– 3; – 1; 1; 2; 4; 5} và B = {– 2; – 1; 0; 2; 3; 5}. Tập hợp A\B:
A. A \ B = {– 3; 1; 4};
B. A \ B = { – 2; 0; 3};
C. A \ B = {– 1; 2; 5};
D.
Câu 9. Tập hợp A = {x ∈ ℝ| – 2 ≤ x < 0} viết lại dưới dạng khác là:
A. A = (– 2; 0];
B. A = [– 2; 0];
C. A = [– 2; 0);
D. A = {– 2; – 1}.
Câu 10. Khẳng định nào sau đây đúng?
A. Đồ thị của một hàm số chẵn nhận trục hoành làm trục đối xứng.
B. Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
C. Đồ thị của một hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.
D. Đồ thị của một số chẵn đi qua gốc tọa độ.
Câu 11. Hai điểm A, B nằm trên đồ thị hàm số y = |x| và đối xứng với nhau qua trục tung. Biết >, diện tích S của tam giác OAB là (biết O là gốc tọa độ, tham khảo đồ thị hàm số y = |x| ở hình vẽ bên).
A. ;
B. ;
C. ;
D. .
Câu 12. Cho Tọa độ của vectơ là:
A. (1; – 1);
B. (– 2; 1);
C. (4; – 2);
D. (– 3; 5).
Câu 13. Cho hình vuông ABCD. Có bao nhiêu vectơ cùng phương với vectơ :
A. 1;
B. 2;
C. 3;
D. 0.
Câu 14. Giá trị nào dưới đây là nghiệm của phương trình ?
A. x = 0;
B. x = – 1;
C. x = 0 và x = – 1;
D. Không tồn tại x là nghiệm của phương trình.
Câu 15. Cho tam giác ABC vuông tại A, AB = 2, AC = 5, .Tính :
A. 7,4;
B. – 7,4;
C. 4,4;
D. – 4,4.
Câu 16. Cho parabol (P):
Hình vẽ trên là đồ thị của hàm số bậc hai nào dưới đây:
A. y = 3x2 – 6x – 1;
B. y = x2 – 2x – 1;
C. y = – x2 + 2x + 1;
D. y = – 3x2 + 6x – 1.
Câu 17. Hàm số nào sau đây là hàm số lẻ?
A. f(x) = x3 + 1;
B. f(x) = 2x4 + 3;
C. f(x) = |x|;
D. f(x) = x3.
Câu 18. Trong các phát biểu sau, phát biểu nào đúng?
A. Tập nghiệm phương trình là tập nghiệm của phương trình f(x) = g(x);
B. Tập nghiệm phương trình là tập nghiệm của phương trình [f(x)]2 = [g(x)]2;
C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Câu 19. Cho tứ giác ABCD. Xác định điểm M thỏa mãn:
A. M là điểm thỏa mãn MA = MG;
B. M là trung điểm của AG;
C. M thuộc đoạn AG thỏa mãn MA = 3 MG;
D. M thuộc trung trực của đoạn thẳng AG.
Câu 20. Cho tứ giác ABC có AB = 5, AC = 4, . Khi đó độ dài BC khoảng:
A. 42,4;
B. 6,5;
C. 3;
D. 3,2.
Câu 21. Gọi S là tập nghiệm của bất phương trình – x2 + 2x – 4 ≤ 0. Khi đó S bằng:
A. ℝ;
B. ℝ\{2; 4};
C. ∅;
D. {2; 4}.
Câu 22. Cho hệ bất phương trình . Điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?
A. M(– 5; 1);
B. N(4; 1);
C. P(0; 1);
D. Q(1; 2).
Câu 23. Với giá trị nào của tham số m thì tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x:
A. m = 2;
B. m = 4;
C. m = 3;
D. m = 6.
Câu 24. Dựa vào đồ thị hàm số bậc hai y = f(x) (như hình vẽ) hãy tìm tập nghiệm của bất phương trình f(x) > 0:
A. [1; 3];
B. (1; 3];
C. (1; 3);
D. {1; 2; 3}.
Câu 25. Nếu hai điểm M và N thỏa mãn: thì độ dài đoạn MN bằng:
A. 8;
B. 4;
C. 2;
D. 64.
B. TỰ LUẬN (3,0 điểm)
Bài 1. (1,0 điểm)
a) Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 5x.
b) Tìm các giá trị của tham số m để phương trình có một nghiệm duy nhất.
Bài 2. (1,0 điểm)
a) Trong mặt phẳng tọa độ Oxy cho hai vectơ và có , và . Tính
b) Cho tam giác ABC , M là trung điểm của cạnh BC điểm N nằm trên cạnh AC sao cho NA = 2NC , D là trung điểm của AN. Chứng minh và
Bài 3. (1,0 điểm) Bác Nam muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 40 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông sao cho độ cao hai thành rãnh bằng nhau. Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2. Bác Nam cần làm rãnh nước có độ cao ít nhất là bao nhiêu xăng – ti – mét để đảm bảo kĩ thuật?
HƯỚNG DẪN ĐÁP ÁN VÀ THANG ĐIỂM
A. TRẮC NGHIỆM (7,0 điểm)
|
Câu 1 |
D |
Câu 6 |
A |
Câu 11 |
B |
Câu 16 |
A |
Câu 21 |
B |
|
Câu 2 |
B |
Câu 7 |
D |
Câu 12 |
B |
Câu 17 |
D |
Câu 22 |
D |
|
Câu 3 |
C |
Câu 8 |
A |
Câu 13 |
C |
Câu 18 |
D |
Câu 23 |
C |
|
Câu 4 |
B |
Câu 9 |
C |
Câu 14 |
B |
Câu 19 |
B |
Câu 24 |
C |
|
Câu 5 |
A |
Câu 10 |
B |
Câu 15 |
B |
Câu 20 |
B |
Câu 25 |
B |
Hướng dẫn đáp án chi tiết
Câu 1. Trục đối xứng của parabol y = x2 + 3x – 1 là đường thẳng:
Đáp án đúng là D
Parabol y = x2 + 3x – 1 có trục đối xứng là đường thẳng .
Câu 2. Cho α là góc nhọn. Khẳng định nào sau đây đúng?
Đáp án đúng là B
Vì α là góc nhọn nên sinα > 0 và cosα > 0
⇒ cotα =
Vậy chọn đáp án B.
Câu 3. Cho hình bình hành ABCD. Khẳng định nào sau đây đúng?
Đáp án đúng là C
Lấy điểm E sao cho ABDE là hình bình hành, khi đó ,
Suy ra AB = ED mà AB = CD nên DE = DC hay D là trung điểm của EC.
Ta có: (quy tắc hình bình hành).
Câu 4. Cho tam giác ABC vuông tại A, AB = 2, . Độ dài của vectơ gần với giá trị nào nhất sau đây:
A. 2,1;
B. 6,5;
C. 2,5;
D. 6,0.
Đáp án đúng là B
Ta có:
⇒
Xét tam giác ABC vuông tại A có:
cosB =
⇔ cos72° =
⇔ BC = .
Vậy độ dài của vectơ gần vớ 6,5.
Câu 5. Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là:
A. ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0;
B. ∀x ∈ ℝ, x3 – 2x + 1 < 0”;
C. ∃x ∈ ℝ, x3 – 2x + 1 ≥ 0”;
D. ∀x ∈ ℝ, x3 – 2x + 1 > 0”.
Đáp án đúng là A
Mệnh đề phủ định của mệnh đề “∃x ∈ ℝ, x3 – 2x + 1 < 0” là ∀x ∈ ℝ, x3 – 2x + 1 ≥ 0.
Câu 6. Cho hai vectơ đều khác vectơ Tích vô hướng của và được xác định bởi công thức
Đáp án đúng là A
Tích vô hướng của và được xác định bởi công thức
Câu 7. Cho hình bình hành ABCD, có M là trung điểm của BC, G là trọng tâm của tam giác ABC (tham khảo hình vẽ bên). Khi đó. Vậy k bằng:
A. ;
B. ;
C. ;
D. k = 3.
Đáp án đúng là D
Vì G là trọng tâm tam giác ABC nên ta có: .
Mặt khác ABCD là hình bình hành, M là trung điểm của BC nên
⇒ hay.
Vậy k = 3.
Câu 8. Cho hai tập hợp A = {– 3; – 1; 1; 2; 4; 5} và B = {– 2; – 1; 0; 2; 3; 5}. Tập hợp A\B:
A. A \ B = {– 3; 1; 4};
B. A \ B = { – 2; 0; 3};
C. A \ B = {– 1; 2; 5};
D. A \ B = {-3;-1; 2; 5}.
Đáp án đúng là A
Ta có tập hợp A \ B là tập hợp các phần tử thuộc tập hợp A nhưng không thuộc tập hợp B nên khi đó ta có: A \ B = {– 3; 1; 4}.
Câu 9. Tập hợp A = {x ∈ ℝ| – 2 ≤ x < 0} viết lại dưới dạng khác là:
A. A = (– 2; 0];
B. A = [– 2; 0];
C. A = [– 2; 0);
D. A = {– 2; – 1}.
Đáp án đúng là C
Ta có: A = {x ∈ ℝ| – 2 ≤ x < 0} = [– 2; 0).
Câu 10. Khẳng định nào sau đây đúng?
A. Đồ thị của một hàm số chẵn nhận trục hoành làm trục đối xứng.
B. Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
C. Đồ thị của một hàm số chẵn nhận gốc tọa độ làm tâm đối xứng.
D. Đồ thị của một số chẵn đi qua gốc tọa độ.
Đáp án đúng là B
Đồ thị của một hàm số chẵn nhận trục tung làm trục đối xứng.
Câu 11. Hai điểm A, B nằm trên đồ thị hàm số y = |x| và đối xứng với nhau qua trục tung. Biết, diện tích S của tam giác OAB là (biết O là gốc tọa độ, tham khảo đồ thị hàm số y = |x| ở hình vẽ bên).
Đáp án đúng là B
Vì A và B đối xứng với nhau qua Oy nên AB ⊥ Oy
Mà Ox ⊥ Oy nên AB // Ox
Kẻ AH vuông góc với Ox và gọi K là trung điểm của AB.
Ta có nên AK = KB = hay OH = . Suy ra xA = .
Mặt khác A thuộc vào đồ thị hàm số nên yA = |xA| = .
⇒ OK =
Diện tích tam giác OAB là: SOAB = (đvdt).
Vậy diện tích tam giác OAB là .
Câu 12. Cho Tọa độ của vectơ là:
A. (1; – 1);
B. (– 2; 1);
C. (4; – 2);
D. (– 3; 5).
Đáp án đúng là B
Ta có:
;
.
Khi đó: .
Câu 13. Cho hình vuông ABCD. Có bao nhiêu vectơ cùng phương với vectơ :
A. 1;
B. 2;
C. 3;
D. 0.
Đáp án đúng là C
Các vectơ cùng phương là các vectơ có giá song song hoặc trùng nhau. Do đó các vectơ cùng phương với vectơ là: , .
Vậy có 3 vec tơ cùng phương với vectơ .
Câu 14. Giá trị nào dưới đây là nghiệm của phương trình ?
A. x = 0;
B. x = – 1;
C. x = 0 và x = – 1;
D. Không tồn tại x là nghiệm của phương trình.
Đáp án đúng là B
Xét phương trình
⇔ = – 1 – x (điều kiện – 1 – x ≥ 0 ⇔ x ≤ – 1)
⇔ 1 – x2 = x2 + 2x + 1
⇔ 2x2 + 2x = 0
⇔ ⇔
Vậy x = – 1 là nghiệm của phương trình đã cho.
Câu 15. Cho tam giác ABC vuông tại A, AB = 2, AC = 5, .Tính :
A. 7,4;
B. – 7,4;
C. 4,4;
D. – 4,4.
Đáp án đúng là B
Câu 16. Cho parabol (P):
Hình vẽ trên là đồ thị của hàm số bậc hai nào dưới đây:
A. y = 3x2 – 6x – 1;
B. y = x2 – 2x – 1;
C. y = – x2 + 2x + 1;
D. y = – 3x2 + 6x – 1.
Đáp án đúng là A
Gọi hàm số cần tìm có dạng y = ax2 + bx + c (a ≠ 0)
Quan sát hình vẽ ta có:
- Đồ thị hàm số cắt trục Oy tại điểm B(0; – 1) nên thay tọa độ điểm B vào hàm số ta được c = – 1.
- Tọa độ điểm đỉnh I(1; – 4)
Khi đó:
Và
Thay b = – 2a vào biểu thức trên ta được: 4a2 + 4a = 16a ⇔ 4a2 – 12a = 0 ⇔ a = 0 (không TM) hoặc a = 3 (TM).
⇒ b = – 2.3 = – 6 .
Vậy hàm số cần tìm là: y = 3x2 – 6x – 1.
Câu 17. Hàm số nào sau đây là hàm số lẻ?
A. f(x) = x3 + 1;
B. f(x) = 2x4 + 3;
C. f(x) = |x|;
D. f(x) = x3.
Đáp án đúng là D
+) Xét hàm số f(x) = x3 + 1
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = (– x)3 + 1 = – x3 + 1.
Do đó f(x) không chẵn cũng không lẻ.
+) Xét hàm số f(x) = 2x4 + 3
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = 2(– x)4 + 3 = 2x4 + 3 = f(x).
Do đó f(x) là hàm chẵn.
+) Xét hàm số f(x) = |x|
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = |– x| = |x| = f(x).
Do đó f(x) là hàm chẵn.
+) Xét hàm số f(x) = x3
Tập xác định: D = ℝ
Lấy – x ∈ D, khi đó f(– x) = (– x)3 = – x3 = – f(x).
Do đó f(x) là hàm lẻ.
Câu 18. Trong các phát biểu sau, phát biểu nào đúng?
A. Tập nghiệm phương trình là tập nghiệm của phương trình f(x) = g(x);
B. Tập nghiệm phương trình là tập nghiệm của phương trình [f(x)]2 = [g(x)]2;
C. Mọi nghiệm của phương trình f(x) = g(x) đều là nghiệm của phương trình ;
D. Tập nghiệm của phương trình là tập hợp các nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Đáp án đúng là D
Xét phương trình
Điều kiện xác định f(x) ≥ 0 hoặc g(x) ≥ 0
Bình phương hai vế của phương trình đã cho ta được: f(x) = g(x)
Vì vậy tập nghiệm của phương trình là tập hợp các nghiệm của phương trình f(x) = g(x) thỏa mãn bất phương trình f(x) ≥ 0 (hoặc g(x) ≥ 0).
Câu 19. Cho tứ giác ABCD. Xác định điểm M thỏa mãn:
A. M là điểm thỏa mãn MA = MG;
B. M là trung điểm của AG;
C. M thuộc đoạn AG thỏa mãn MA = 3 MG;
D. M thuộc trung trực của đoạn thẳng AG.
Đáp án đúng là B
Gọi G là trọng tâm tam giác BCD, khi đó ta có:
Vậy M là trung điểm của GA.
Câu 20. Cho tứ giác ABC có AB = 5, AC = 4, . Khi đó độ dài BC khoảng:
A. 42,4;
B. 6,5;
C. 3;
D. 3,2.
Đáp án đúng là B
Xét tam giác ABC, có:
BC2 = AB2 + AC2 – 2AB.AC.cos
= 42 + 52 – 2.4.5.cos92°
≈ 42,4
⇒ BC = 6,5
Vậy BC = 6,5.
Câu 21. Gọi S là tập nghiệm của bất phương trình – x2 + 2x – 4 ≤ 0. Khi đó S bằng:
A. ℝ;
B. ℝ\{2; 4};
C. ∅;
D. {2; 4}.
Đáp án đúng là B
Xét bất phương trình – x2 + 2x – 4 ≤ 0 có a = – 1 < 0 và ∆’ = (– 1)2 – (– 1)(– 4) = – 3 < 0.
Dựa vào định lí dấu tam thức bậc hai ta có – x2 + 2x – 4 ≤ 0 ∀x
Vậy tập nghiệm của bất phương trình là S = ℝ.
Câu 22. Cho hệ bất phương trình>. Điểm nào thuộc miền nghiệm của hệ bất phương trình đã cho?
A. M(– 5; 1);
B. N(4; 1);
C. P(0; 1);
D. Q(1; 2).
Đáp án đúng là D
Xét hệ bất phương trình
Thay lần lượt tọa độ các điểm M, N, P, Q vào hệ bất phương trình ta có:
Tọa độ điểm M không thỏa mãn BPT (3);
Tọa độ điểm N không thỏa mãn BPT (2);
Tọa độ điểm P không thỏa mãn BPT (3);
Tọa độ điểm Q thỏa mãn tất cả các BPT của hệ nên thuộc vào miền nghiệm.
Vậy chọn D.
Câu 23. Với giá trị nào của tham số m thì tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x:
A. m = 2;
B. m = 4;
C. m = 3;
D. m = 6.
Đáp án đúng là C
Xét tam thức f(x) = – x2 – 3x + m – 5 có a = – 1 và ∆ = (– 3)2 – 4.(– 1).(m – 5) = 9 + 4m – 20 = 4m – 11.
Để tam thức f(x) = – x2 – 3x + m – 5 không dương với mọi x thì ∆ ≤ 0
⇔ 4m – 11 ≤ 0
⇔ m ≤
Vậy m = 2 thỏa mãn điều kiện bài toán.
Câu 24. Dựa vào đồ thị hàm số bậc hai y = f(x) (như hình vẽ) hãy tìm tập nghiệm của bất phương trình f(x) > 0:
A. [1; 3];
B. (1; 3];
C. (1; 3);
D. {1; 2; 3}.
Đáp án đúng là C
Quan sát hình vẽ ta thấy với x ∈ (1; 3) thì đồ thị hàm số nằm phía trên trục hoành.
Hay f(x) > 0 khi x ∈ (1; 3).
Vậy tập nghiệm của bất phương trình f(x) > 0 là S = (1; 3).
Câu 25. Nếu hai điểm M và N thỏa mãn: thì độ dài đoạn MN bằng:
A. 8;
B. 4;
C. 2;
D. 64.
Đáp án đúng là B
Ta có: = MN.NM. = MN2.cos180o = -MN2
Suy ra – MN2 = – 16 ⇔ MN =
Vậy MN = 4.
B. TỰ LUẬN (5,0 điểm)
Bài 1. (2,0 điểm)
a) Lập bảng biến thiên và vẽ đồ thị của hàm số y = x2 – 5x.
b) Tìm các giá trị của tham số m để phương trình có một nghiệm duy nhất.
a) Xét hàm số y = x2 – 5x, có: a = 1, b = – 5, c = 0 và ∆ = (– 5)2 – 4.1.0 = 25
Khi đó, ta có:
- Điểm đỉnh I có xI = ; yI = ;
- a = 1 > 0 .
Do đó ta có bảng biến thiên sau:
Vậy hàm số sẽ đồng biến trên khoảng, hàm số sẽ nghịch biến trên khoảng .
b) Xét hàm số y = x2 – 5x, có: a = 1, b = – 5, c = 0 và ∆ = (– 5)2 – 4.1.0 = 25
Khi đó, ta có:
- Điểm đỉnh I có xI = ; yI = . Do đó I.
- Trục đối xứng của đồ thị là .
- Đồ thị hàm số cắt trục tung tại điểm có tọa độ (0; 0).
- Đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (0; 0) và (5; 0).
- Ta có a = 1 > 0 bề lõm của đồ thị quay lên trên.
b) Xét phương trình >(*)
Điều kiện x + 1 ≥ 0 ⇔ x ≥ – 1
(*) ⇔ x2 – (2m – 1)x – m2 + 5m + = x2 + 2x + 1
⇔ (2m + 1)x + m2 – 5m – = 0
+) TH1: 2m + 1 = 0 ⇔ m = . Khi đó ta có:
⇔ 0.x + 0 = 0 (luôn đúng) với mọi x ≥ – 1
Do đó m = thỏa mãn.
+) TH1: 2m + 1 ≠ 0 ⇔ m ≠ . Khi đó ta có:
(2m + 1)x + m2 – 5m – = 0
⇔ x =
Để phương trình có nghiệm thì
⇔ m2 – 5m – ≥ – 2m – 1
⇔ m2 – 3m – ≥ 0
Xét tam thức bậc hai f(m) = m2 – 3m – , có a = 1 và ∆ = (– 3)2 – 4.1. = 16 > 0 suy ra f(m) có hai nghiệm m1 = và m2 = .
Dựa vào định lí dấu tam thức bậc hai ta có:
f(m) ≥ 0 ⇔ m ≤ hoặc m ≥ .
Suy ra m < hoặc m ≥ .
Vậy với m ≤ hoặc m ≥ thì phương trình có nghiệm.
Bài 2. (1,5 điểm)
a) Trong mặt phẳng tọa độ Oxy cho hai vectơ và có , và . Tính
b) Cho tam giác ABC, M là trung điểm của cạnh BC điểm N nằm trên cạnh AC sao cho NA = 2NC , D là trung điểm của AN. Chứng minh và
Hướng dẫn giải
a) Ta có:
⇔
Vậy .
b)
Ta có hình vẽ sau:
+) Ta có AC = 3DA và và là hai vec tơ ngược hướng nên
Hay .
+) Ta có:
⇔
⇔
⇔
⇔ .
Bài 3. (1,5 điểm) Bác Nam muốn uốn tấm tôn phẳng có dạng hình chữ nhật với bề ngang 42 cm thành một rãnh dẫn nước bằng cách chia tấm tôn đó thành ba phần rồi gấp hai bên lại theo một góc vuông sao cho độ cao hai thành rãnh bằng nhau. Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2. Bác Nam cần làm rãnh nước có độ cao ít nhất là bao nhiêu xăng – ti – mét để đảm bảo kĩ thuật?
Hướng dẫn giải
Chia tấm tôn đó thành ba phần theo các kích thước x (cm), 42 – x (cm) và x (cm).
Khi gấp hai bên lại ta được rãnh dẫn nước có mặt cắt ngang có kích thước là x (cm) và 42 – x (cm).
Diện tích của mặt cắt ngang là x.(42 – x) = – x2 + 42x (cm2).
Để đảm bảo kĩ thuật, diện tích mặt cắt ngang của rãnh dẫn nước phải lớn hơn hoặc bằng 160 cm2 nên ta có:
– x2 + 42x ≥ 160
⇔ – x2 + 42x – 160 ≥ 0
Xét tam thức bậc hai f(x) = – x2 + 42x – 160 có a = – 1, b = 42, c = – 160 và ∆ = 422 – 4.(– 1).(– 160) = 1124 > 0.
Suy ra f(x) có hai nghiệm x1 = và x2 = .
Áp dụng định lí dấu của tam thức bậc hai ta được:
f(x) ≥ 0 khi 2,12 ≤ x ≤ 18,88
Vậy rãnh nước phải có độ cao ít nhất khoảng 2,12 cm.
Đề thi học kì 1 Toán lớp 10 Cánh diều có đáp án - Đề 3
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
Năm học ...............
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 3)
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1: Cho tam giác ABC. Gọi M, N lần lượt là trung điểm của các cạnh AB, AC. Hỏi cặp vectơ nào sau đây cùng hướng?
Câu 2: Trong các câu sau, câu nào không là mệnh đề ?
A. 12 là số nguyên tố;
B. không chia hết cho 2;
C. x2 là số thực không âm;
D. 10 là số nguyên tố.
Câu 3: Cặp số nào sau đây không là nghiệm của bất phương trình ?
Câu 4: Cách viết nào sau đây là đúng?
A. (1; 2] ∈ ℝ;
B. {1; 2} ∈ ℝ;
C. 1 ∈ ℝ;
D. [1; 2] ∈ ℝ.
Câu 5: Cho hình vẽ sau:
Tích vô hướng của hai vectơ nào bằng 0?
Câu 6. Cho hình thoi cạnh a và . Độ dài vectơ là
Câu 7. Tính
A. ;
B. ;
C. ;
D. .
Câu 8: Với α ∈ (120°; 270°) thì giá trị lượng giác nào dưới đây nhận giá trị âm?
A. sinα;
B. cosα;
C. tanα;
D. cotα.
Câu 9. Trong các bất phương trình sau, bất phương trình bậc nhất hai ẩn là
Câu 10. Cho đồ thị hàm số sau:
Đồ thị hàm số trên là của hàm số nào dưới đây?
A. x2 – 4x – 2;
B. – x2 + 4x – 2;
C. – x2 – 4x + 2;
D. x2 – 4x + 2.
Câu 11. Cho tam giác ABC, có G là trọng tâm tam giác, M là điểm bất kì. Biểu thức nào sau đây là đúng?
Câu 12. Cho đồ thị hàm số:
Hàm số đồng biến trên khoảng
A. (– 4; 1);
B. (– 2; 0);
C. (– 4; – 2);
D. (– 4; +∞).
Câu 13. Hàm số f(x) = x2 – 2x + 1 nhận giá trị dương khi
A. x ∈ ℝ;
B. x ∈ ;
C. x > 1;
D. x ≠ 1.
Câu 14. Cặp số (0; 1) là nghiệm của hệ bất phương trình nào sau đây?
Câu 15. Cho hàm số y = f(x) có bảng biến thiên sau:
Tập giá trị của hàm số f(x) là:
A. [– 3; 5];
B. [– 3; +∞);
C. (– ∞; 5];
D. (– ∞; +∞).
Câu 16. Cho các bất phương trình sau:
– 2x + 1 < 0; ; ; y2 + x2 – 2x < 0.
Có bao nhiêu bất phương trình không là bất phương trình bậc hai một ẩn?
A. 0;
B. 1;
C. 2;
D. 3.
Câu 17. Hàm số bậc hai y = 2x2 – x có trục đối xứng là
Câu 18. Tập nghiệm của bất phương trình x2 – 5x + 6 < 0 là
A. S = (2; 3);
B. S = (– ∞; 2);
C. S = (3; +∞);
D. S = (– ∞; 2) ∪ (3; +∞).
Câu 19. Để giải phương trình: cần điều kiện:
A. ;
B. x ≤ – 1 hoặc x ≥ 1;
C. x ≥ 1;
D. x ≤ – 1.
Câu 20. Lớp 10B có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Sử, 6 em không thích môn nào, 6 em thích cả Sử và Toán, 8 em thích cả Văn và Toán, 5 em thích cả ba môn. Số học sinh thích cả Văn và Sử là
A. 5;
B. 10;
C. 12;
D. 15.
Câu 21: Tam giác có và . Bán kính của đường tròn ngoại tiếp tam giác ABC là
A. .
B. .
C. .
D. .
Câu 22. Trong các công thức dưới đây, công thức nào tính diện tích tam giác ABC là đúng?
A. SABC = ;
B. SABC = ;
C. SABC = pR;
D. SABC = a.ha.
Câu 23. Tính giá trị biểu thức: cos20° + cos40° + cos60° + ... + cos160° + cos180°.
A. – 1;
B. 1;
C. 2;
D. 0.
Câu 24: Cho hàm số . Tập xác định D của hàm số là
A. D = [0; +∞) \ {1; 4};
B. D = [0; +∞) \ {4};
C. D = [– 2; +∞) \ {1; 4};
D. D = [– 2; +∞) \ {1}.
Câu 25. Cho tam giác có . Tam giác ABC là
A. tam giác nhọn;
B. tam giác tù;
C. tam giác vuông;
D. tam giác đều.
Câu 26. Cho tam giác ABC có M là trung điểm của AC, N là trung điểm của BC và AB = a. Độ dài vectơ bằng
A. a;
B. ;
C. ;
D. .
Câu 27. Cho 90° < α < 180°. Xác định dấu của biểu thức M = sin(90° – α).cot(180° + α).
A. M ≥ 0;
B. M ≤ 0;
C. M > 0;
D. M < 0.
Câu 28. Cho tam giác ABC đều cạnh bằng a, AH là đường cao. Tính
A. ;
B. ;
C. ;
D. a2.
Câu 29. Cho tứ giác ABCD, có I, J lần lượt là trung điểm của AB và CD. Ta có . Khi đó a – b bằng
A. 0;
B. 1;
C. ;
D. .
Câu 30. Cho phương trình: . Số nghiệm của phương trình là
A. 0;
B. 1;
C. 2;
D. vô số nghiệm.
II. PHẦN TỰ LUẬN (3,0 điểm)
Bài 1. (1 điểm)
Một rạp chiếu phim có sức chứa 1 000 người. Với giá vé là 40 000 đồng, trung bình sẽ có khoảng 300 người đến rạp xem phim mỗi ngày. Để tăng số lượng vé bán ra, rạp chiếu phim đã khảo sát thị trường và thấy rằng giá vé cứ giảm 10 000 đồng thì sẽ có thêm 100 người đến rạp mỗi ngày.
a) Tìm công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé mỗi ngày của rạp chiếu phim khi giá vé là x nghìn đồng.
b) Tìm mức giá vé để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất.
Bài 2. (1,0 điểm)
a) Giải phương trình: .
b) Tìm m để hàm số f(x) = x2 – 2(m + 3)x – 4m + 1 > 0 với mọi số thực x.
Bài 3. (1,0 điểm) Cho tam giác ABC, gọi I và J là hai điểm được xác định bởi.
a) Tính .
b) Chứng minh đường thẳng IJ đi qua trọng tâm G của tam giác ABC.
HƯỚNG DẪN ĐÁP ÁN VÀ THANG ĐIỂM
I. PHẦN TRẮC NGHIỆM (7 ĐIỂM)
Câu 1.
Ta có hình vẽ:
+) Hai vectơ và có cùng giá là đường thẳng AB và cùng chiều hướng xuống dưới nên hai vec tơ này cùng hướng. Do đó A đúng.
+) Hai vectơ và có giá là hai đường thẳng song song (theo tính chất đường trung bình) nhưng khác hướng. Do đó B sai.
+) Hai vectơ và là hai vectơ đối nhau nên không cùng hướng. Do đó C sai.
+) Hai vectơ và có cùng giá là đường thẳng AC nhưng ngược hướng. Do đó D sai.
Câu 2.
Đáp án đúng là: B
Câu “n không chia hết cho 2” là mệnh đề chứa biến tính đúng sai phụ thuộc vào biến n.
Câu 3.
Đáp án đúng là: B
+) Thay x = 0 và y = vào bất phương trình ta được: là mệnh đề sai. Do đó A sai.
+) Thay x = – 1 và y = vào bất phương trình ta được: là mệnh đề đúng. Do đó B đúng.
+) Thay x = 4 và y = vào bất phương trình ta được: là mệnh đề sai. Do đó C sai.
+) Thay x = – 2 và y = vào bất phương trình ta được: là mệnh đề sai. Do đó D sai.
Câu 4.
Đáp án đúng là: C
Ta có: (1; 2], {1; 2}, [1; 2] là các tập hợp nên ta có quan hệ tập con (1; 2] ⊂ ℝ, {1; 2} ⊂ ℝ, [1; 2] ⊂ ℝ. Do đó A, B, D sai.
Còn 1 là một số thực nên 1 là một phần tử của tập hợp ℝ, ta viết: 1 ∈ ℝ. Do đó C đúng.
Câu 5.
Đáp án đúng là: D
Ta có: AB ⊥ BD nên .
Câu 6.
Đáp án đúng là: D
Xét tam giác ABC, có: AB = AD = a nên tam giác ABC cân tại A mà do đó ABC đều.
Vì vậy .
Câu 7.
Đáp án đúng là: D
Ta có: .
Câu 8.
Đáp án đúng là: B
Ta có α ∈ (120°; 270°) nên cosα < 0, còn sinα có thể âm hoặc dương. Do đó cotα, tanα có thể âm hoặc dương.
Vậy với α ∈ (120°; 270°) thì cosα nhận giá trị âm.
Câu 9.
Đáp án đúng là: D
Bất phương trình bậc nhất hai ẩn có dạng ax + by ≥ c (ax + by ≤ c, ax + by > c, ax + by < c ) với a, b, c là các số thực.
Do đó chỉ có bất phương trình là thỏa mãn.
Câu 10.
Đáp án đúng là: D
Gọi hàm số bậc hai cần tìm là y = ax2 + bx + c (a ≠ 0).
Ta có giao điểm của đồ thị hàm số với trục tung là (0; 2) suy ra c = 2.
Đồ thị hàm số có điểm điểm I(2; – 2) nên ta có:
(loại a = 0 vì không thỏa mãn điều kiện).
Vì vậy hàm số cần tìm là y = x2 – 4x + 2.
Câu 11.
Đáp án đúng là: D
Ta có: .
Câu 12.
Đáp án đúng là: C
Hàm số đi lên (đồng biến) trên khoảng (– ∞; – 2) và (0; +∞).
Mà (– 4; – 2) ⊂ (– ∞; – 2) nên hàm số cũng đồng biến (– 4; – 2). Do đó C đúng.
Câu 13.
Đáp án đúng là: D
Ta có: x2 – 2x + 1 = (x – 1)2 ≥ 0 với mọi x nên để f(x) > 0 thì x – 1 ≠ 0 ⇔ x ≠ 1.
Câu 14.
Đáp án đúng là: A
+) Thay x = 0 và y = 1 vào lần lượt các bất phương trình trong hệ ta được:
0 – 2.1 = – 2 < 0
0 + 3.1 = 3 > – 2
Là những mệnh đề đúng nên (0; 1) là nghiệm của hệ bất phương trình
Do đó A đúng.
+) Thay x = 0 và y = 1 vào lần lượt các bất phương trình trong hệ ta được:
0 – 2.1 = – 2 > 0
0 + 3.1 = 3 < – 2
Là những mệnh đề sai nên (0; 1) không là nghiệm của hệ bất phương trình Do đó B sai.
+) Thay x = 0 và y = 1 vào lần lượt các bất phương trình trong hệ ta được:
0 – 2.1 = – 2 ≥ 0 là mệnh đề sai
0 – 3.1 = – 3 ≤ – 2 là mệnh đề đúng
Suy ra (0; 1) không là nghiệm của hệ bất phương trình Do đó C sai.
+) Thay x = 0 và y = 1 vào lần lượt các bất phương trình trong hệ ta được:
0 – 2.1 = – 2 ≤ 0 là mệnh đề đúng
0 – 3.1 = – 3 ≥ – 2 là mệnh đề sai
Suy ra (0; 1) không là nghiệm của hệ bất phương trình Do đó D sai.
Câu 15.
Đáp án đúng là: D
Dựa vào bảng biến thiên ta thấy, hàm số nhận giá trị trên tập (– ∞; +∞).
Câu 16.
Đáp án đúng là: D
– 2x + 1 < 0 không là bất phương trình bậc hai một ẩn vì đây là bất phương trình bậc nhất.
có dạng bất phương trình bậc nhất hai ẩn.
không có dạng của bất phương trình bậc hai một ẩn.
y2 + x2 – 2x < 0 là bất phương trình bậc hai nhưng có hai ẩn x và y.
Câu 17.
Đáp án đúng là: B
Hàm số bậc hai y = 2x2 – x có a = 2, b =
Khi đó trục đối xứng của hàm số đã cho là: .
Câu 18.
Đáp án đúng là: A
Xét tam thức f(x) = x2 – 5x + 6, có a = 1 > 0, ∆ = (– 5)2 – 4.1.6 = 1 > 0 nên f(x) có hai nghiệm phân biệt x1 = 2 và x2 = 3.
Áp dụng định lí về dấu tam thức bậc hai ta được:
f(x) < 0 khi x ∈ (2; 3).
Vậy tập nghiệm của bất phương trình đã cho là S = (2; 3).
Câu 19.
Đáp án đúng là: B
Điều kiện xác định của phương trình là: x2 – 1 ≥ 0 ⇔ x2 ≥ 1 ⇔ |x| ≥ 1
⇔ x ≥ 1 hoặc x ≤ – 1.
Câu 20.
Đáp án đúng là: B
Gọi V là tập hợp số học sinh thích môn Văn;
T là tập hợp số học sinh thích môn Toán;
S là tập hợp số học sinh thích môn Sử;
V ∩ T là tập hợp số học sinh vừa thích Văn vừa thích Toán;
S ∩ T là tập hợp số học sinh vừa thích Sử vừa thích Toán;
V ∩ S là tập hợp số học sinh vừa thích Văn vừa thích Sử;
T ∩ V ∩ S là tập hợp số học sinh vừa thích Văn vừa thích Toán, vừa thích Sử;
T ∪ V ∪ S là tập hợp số học sinh thích ít nhất một trong ba môn Toán, Văn, Sử.
Khi đó: |T ∪ V ∪ S| = 45 – 6 = 39, |V| = 25, |T| = 20, |S| = 18, |V ∩ T| = 8, |S ∩ T| = 6, |T ∩ V ∩ S| = 5.
Ta có: |T ∪ V ∪ S| = |V| + |T| + |S| – |V ∩ T| – |S ∩ T| – |V ∩ S| + |T ∩ V ∩ S|
⇔ 39 = 25 + 20 + 18 – 8 – 6 – |V ∩ S| + 5
⇔ |V ∩ S| = 15
Vậy có 15 học sinh vừa thích Văn vừa thích Sử.
Câu 21.
Đáp án đúng là: B
Xét tam giác ABC:
Áp dụng định lí cosin ta được:
BC2 = AB2 + AC2 – 2.AB.AC.cosA
= 32 + 62 – 2.3.6.cos60°
= 27
⇔ BC = 3
Áp dụng định lí sin ta được:
.
Câu 22.
Đáp án đúng là: B
Các công thức tính diện tích tam giác là:
SABC = . Do đó A sai.
SABC = . Do đó B đúng.
SABC = pr. Do đó C sai.
SABC = a.ha = b.hb = c.hc. Do đó D sai.
Câu 23.
Đáp án đúng là: A
cos20° + cos40° + cos60° + ... + cos160° + cos180°
= (cos20° + cos160°) + (cos40° + cos140°) + ... + (cos80° + cos100°) + cos180°
= (cos20° – cos20°) + (cos40° – cos40°) + ... + (cos80° – cos80°) + cos180°
= 0 + 0 + ... + 0 + (– 1)
= – 1.
Câu 24.
Đáp án đúng là: B
Điều kiện xác định của hàm số:
Vậy tập xác định của hàm số là: D = [0; +∞) \ {4}.
Câu 25.
Đáp án đúng là: A
Ta có AB < BC < AC nên .
Áp dụng hệ quả của định lí cosin ta được:
< 90°.
Suy ra góc lớn nhất của tam giác ABC là góc nhọn nên hai góc còn lại cũng nhọn. Vì vậy tam giác ABC nhọn.
Câu 26.
Đáp án đúng là: C
Vì (N là trung điểm của BC)
Xét tam giác ABC, có:
M là trung điểm của AC
N là trung điểm của BC
Suy ra MN là đường trung bình của tam giác ABC
Vì vậy .
Câu 27.
Đáp án đúng là: C
Ta có: M = sin(90° – α).cot(180° + α)
= cosα . (– cotα)
= cosα .
=
Vì 90° < α < 180° nên sinα > 0
Mà cos2α ≥ 0 với mọi 90° < α < 180°
Do đó hay M ≤ 0.
Câu 28.
Đáp án đúng là: A
Xét tam giác đều ABC, có: AB = a, AH =
Ta lại có AH là đường cao nên cũng là đường phân giác của
Câu 29.
Đáp án đúng là: A
Ta có:
⇒ a = và b =
⇒ a – b = = 0.
Câu 30.
Đáp án đúng là: A
Bình phương hai vế của phương trình trên, ta được:
x2 – 5x + 1 = x – 7
⇔ x2 – 6x + 8 = 0
⇔
Thay x = 4 và x = 2 vào phương trình đã cho, ta thấy cả hai giá trị đều không thỏa mãn.
Vậy phương trình vô nghiệm.
II. PHẦN TỰ LUẬN (3,0 điểm)
Bài 1. (1 điểm)
Hướng dẫn giải
a) Ta có x là giá vé nên x > 0.
Số tiền giảm giá so với giá vé cũ là: 40 – x (nghìn đồng).
Số người đến rạp tăng lên: [(40 – x) : 10] . 100 = 400 – 10x (người).
Tổng số người đến rạp sau giảm giá là: 300 + 400 – 10x = 700 – 10x (người).
Doanh thu từ tiền bán vé sau giảm giá là: (700 – 10x).x = – 10x2 + 700x (nghìn đồng).
Khi đó công thức của hàm số R(x) mô tả doanh thu từ tiền bán vé là:
R(x) = – 10x2 + 700x.
b) Xét hàm số bậc hai R(x) = – 10x2 + 700x, có:
Tọa độ điểm đỉnh là: xI = , yI = .
Ta có: a = – 10 < 0 nên ta có bảng biến thiên:
Suy ra hàm số đạt giá trị lớn nhất là 12 250 tại x = 35.
Vậy để doanh thu từ tiền bán vé mỗi ngày của rạp là lớn nhất thì rạp cần bán vé với giá 35 nghìn đồng.
Bài 2. (1,0 điểm)
Hướng dẫn giải
a) (*)
Điều kiện – x + 9 ≥ 0 ⇔ x ≤ 9
Bình phương hai vế của phương trình (*) ta được:
9(x2 – 2x – 3) = x2 – 18x + 81
⇔ 9x2 – 18x – 27 = x2 – 18x + 81
⇔ 8x2 = 108
⇔ x2 = >
⇔ x = .
Vậy phương trình có nghiệm x = .
b) Xét hàm số f(x) = x2 – 2(m + 3)x – 4m + 1 có a = 1 > 0, ∆’ = (m + 3)2 – (– 4m + 1).1 = m2 + 6m + 9 + 4m – 1 = m2 + 10m + 8.
Để hàm số f(x) = x2 – 2(m + 3)x – 4m + 1 > 0 với mọi số thực x thì .
Vậy .
Bài 3. (1,0 điểm)
Hướng dẫn giải
a) Ta có:
b)
Ta có:
.
Vậy I, J, G thẳng hàng hay IJ đi qua G.
Đề thi học kì 1 Toán lớp 10 Cánh diều có đáp án - Đề 4
Phòng Giáo dục và Đào tạo .....
Đề thi Học kì 1 - Cánh diều
Năm học ...............
Môn: Toán 10
Thời gian làm bài: 90 phút
(Đề số 4)
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
Câu 1: Trong các câu sau, có bao nhiêu câu là không phải là mệnh đề?
a) Huế là một thành phố của Việt Nam.
b) Sông Hương chảy ngang qua thành phố Huế.
c) Hãy trả lời câu hỏi này!
d)
e)
f) Bạn có mang theo máy tính không?
g)
A. 1. B. 2. C. 3. D. 4.
Câu 2: Cho parabol có đồ thị như hình sau
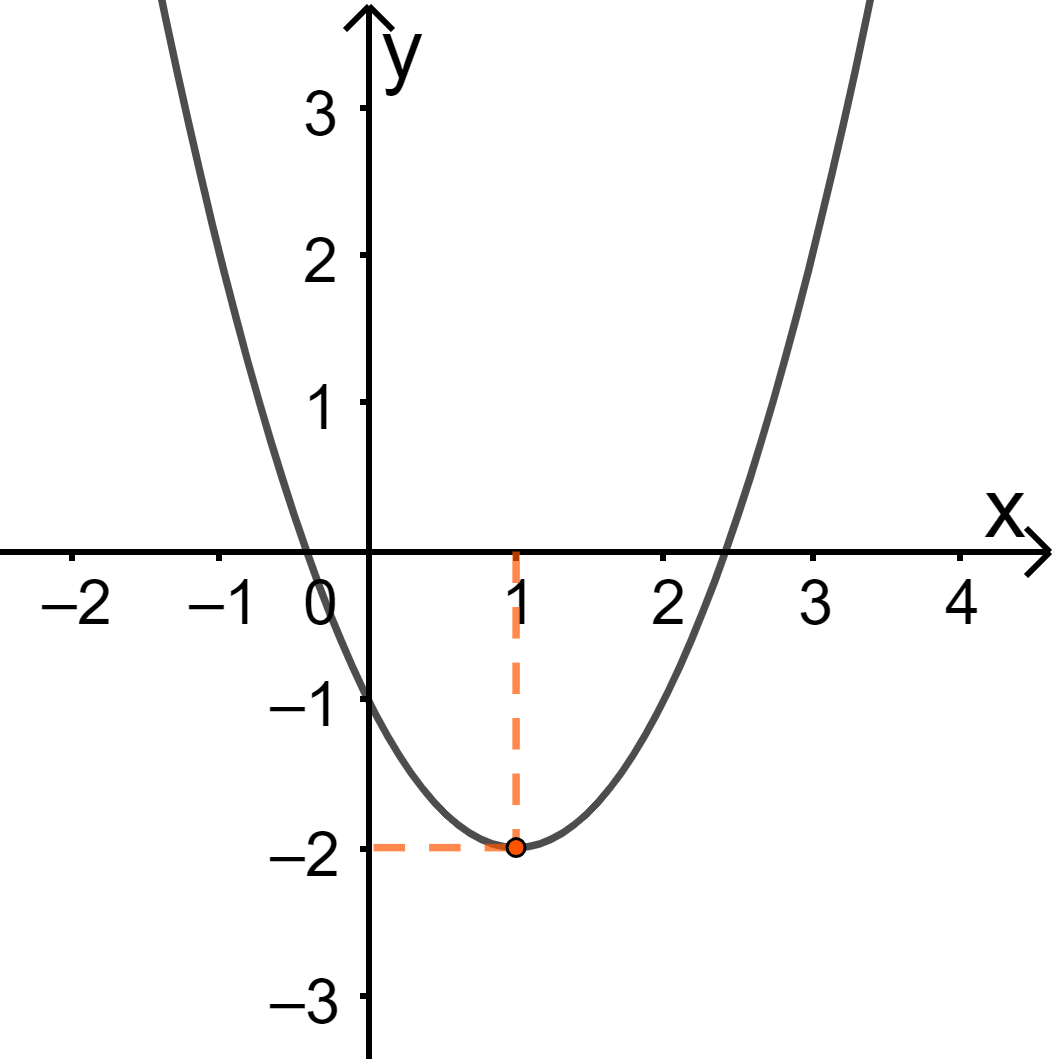
Phương trình của parabol này là
A. . B. . C. . D. .
Câu 3: Cho hình bình hành có là giao điểm của hai đường chéo. Đẳng thức nào sau đây sai?
A. B.
C. D.
Câu 4: Lớp 10E có học sinh giỏi Toán, học sinh giỏi Lý, học sinh giỏi Hóa, học sinh giỏi cả Toán và Lý, học sinh giỏi cả Toán và Hóa, học sinh giỏi cả Lý và Hóa, học sinh giỏi cả môn Toán, Lý, Hóa. Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) của lớp 10E là
A. B. C. D.
Câu 5: Miền nghiệm của bất phương trình: là nửa mặt phẳng chứa điểm:
A. B. C. D.
Câu 6: Phần không tô đậm trong hình vẽ dưới đây (không chứa biên), biểu diễn tập nghiệm của hệ bất phương trình nào trong các hệ bất phương trình sau?
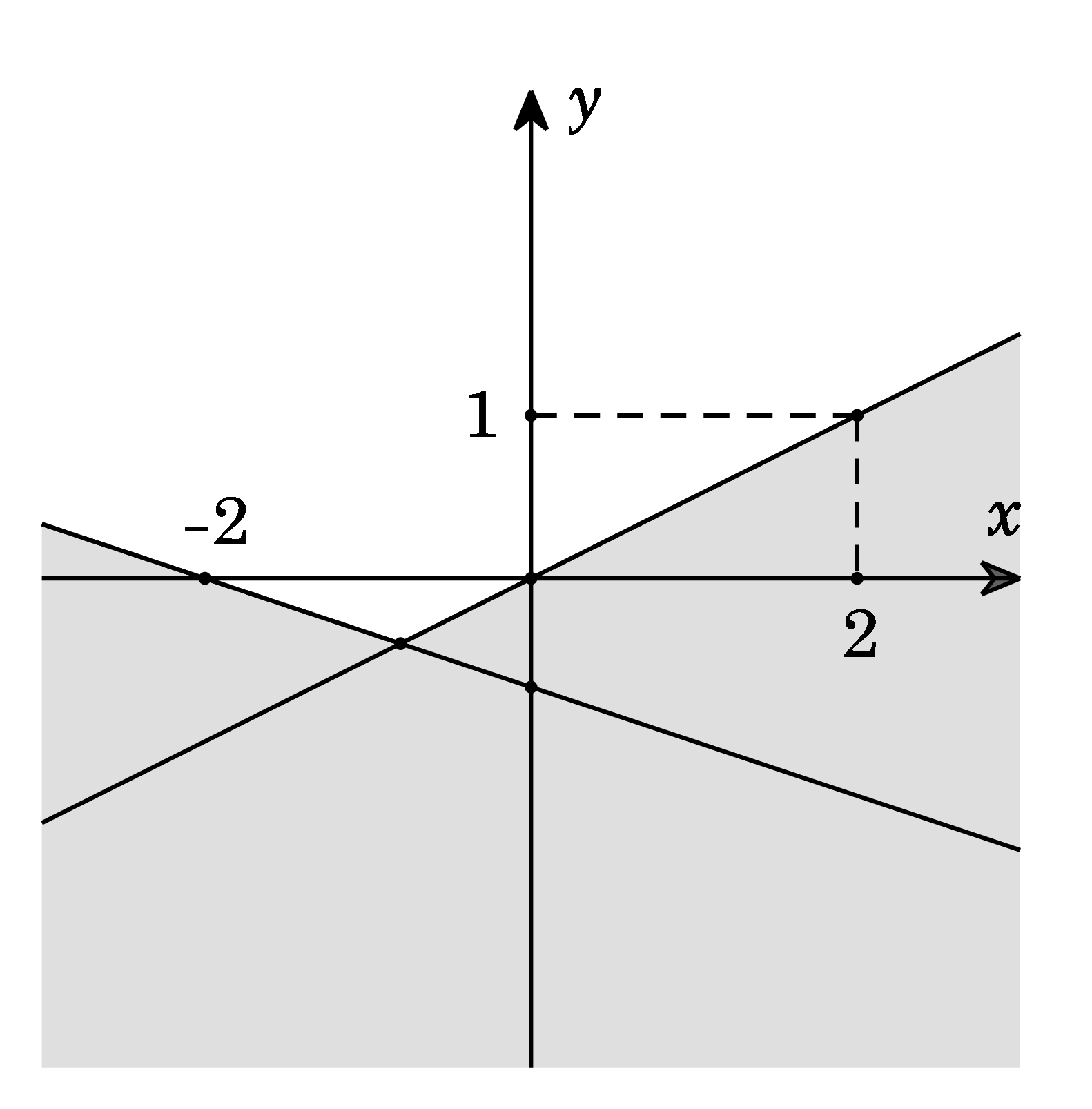
A. B. C. D.
Câu 7: Tam giác có và . Tính bán kính của đường tròn ngoại tiếp tam giác .
A. . B. . C. . D. .
Câu 8: Bảng biến thiên của hàm số là:
A.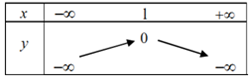 B.
B. 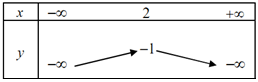
C. 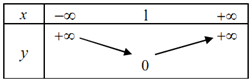 D.
D. 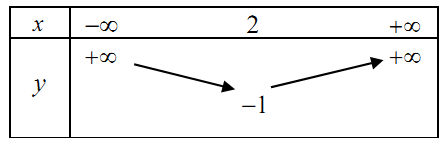
Câu 9: Tính giá trị biểu thức .
A. B. C. D.
Câu 10: Cho hình vuông cạnh . Tính
A. B. C. D.
Câu 11: Tìm tập xác định của hàm số
A. B. C. D.
Câu 12: Cho hàm số . Điểm nào sau đây thuộc đồ thị hàm số:
A. . B. . C. . D. .
Câu 13: Gọi là trọng tâm của . Đặt . Xác định giá trị của để .
A. B. C. D.
Câu 14: Tam giác có . Tính diện tích tam giác .
A. . B. . C. . D. .
Câu 15: Hàm số , đồng biến trong khoảng nào sau đậy?
A. B. C. D.
Câu 16: Cho tam giác đều có cạnh bằng Tính tích vô hướng
A. B. C. D.
Câu 17: Cho tập hợp là ước chung của . Hãy liệt kê các phần tử của tập hợp .
A. B.
C. D.
Câu 18: Cho hai tập hợp Mệnh đề nào sau đây đúng?
A. B. C. D.
Câu 19: Điểm thuộc miền nghiệm của hệ bất phương trìnhnào sau đây?
A. B.
C. D.
Câu 20: Giá trị nhỏ nhất của biểu thức trên miền xác định bởi hệ là
A. B. C. D.
Câu 21: Hàm số bậc hai nào sau đây có đồ thị là parabol có hoành độ đỉnh là và đi qua ?
A. . B. .
C. . D. .
Câu 22: Cho biết Giá trị của bằng bao nhiêu?
A. B. C. D.
Câu 23: Cho tam giác ABC. Trên cạnh BC lấy điểm sao cho . Khi đó, vectơ bằng
A. B. C. D.
Câu 24: Cho hai vecto bất kỳ; . Khẳng định nào sau đây không đúng?
A. B. C. D.
Câu 25: Tam giác vuông tại có cm, cm. Tính bán kính của đường tròn nội tiếp tam giác đã cho.
A. cm. B. cm. C. cm. D. cm.
Phần 2: Tự luận (5 điểm)
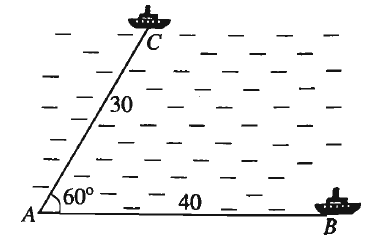
Câu 1: Hai chiếc tàu thủy cùng xuất phát từ một vị trí , đi thẳng theo hai hướng tạo với nhau góc . Tàu chạy với tốc độ hải lí một giờ. Tàu chạy với tốc độ hải lí một giờ. Sau hai giờ, hai tàu cách nhau bao nhiêu hải lí (làm tròn đến số thập phân)?
Câu 2: Cho tam giác ABC. Tìm tập hợp các điểm M thỏa mãn
a)
b)
c)
Câu 3: Tìm parabol (P) biết (P) có đỉnh và giao với Oy tại điểm có tung độ bằng -1. Vẽ đồ thị hàm số tìm được.
----- HẾT -----
HƯỚNG DẪN GIẢI CHI TIẾT
Phần 1: Trắc nghiệm (25 câu – 5 điểm)
| Câu 1-B | Câu 2-C | Câu 3-C | Câu 4-B | Câu 5-C |
| Câu 6-C | Câu 7-C | Câu 8-B | Câu 9-B | Câu 10-D |
| Câu 11-A | Câu 12-A | Câu 13-A | Câu 14-B | Câu 15-C |
| Câu 16-C | Câu 17-C | Câu 18-A | Câu 19-C | Câu 20-C |
| Câu 21-D | Câu 22-D | Câu 23-A | Câu 24-D | Câu 25-A |
Phần 2: Tự luận (5 điểm)
Câu 1 (VD):
Sau giờ tàu đi được hải lí, tàu đi được hải lí. Vậy tam giác có và
Áp dụng định lí côsin vào tam giác ta có
Vậy (hải lí).
Sau giờ, hai tàu cách nhau khoảng 36 hải lí.
Câu 2 (VD):
a) Gọi I là trung điểm ta có:
Vậy tập hợp điểm là đường tròn tâm , bán kính .
b) Gọi là điểm thoả mān:
L là điểm thoả mān:
Ta có:
Tập hợp điểm là đường trung trực của đoạn thẳng .
c) Với I là trung điểm của . Gọi là điểm thoả mān:
Ta có:
const
Vậy tập hợp điểm là đường tròn tâm bán kính .
Câu 3 (VD):
Parabol (P) giao với Oy tại điểm có tọa độ , do đó
(P) có hoành độ đỉnh
Điểm thuộc (P) nên hay
Từ đó ta có hệ phương trình
Vậy parabol cần tìm là
* Vẽ parabol
Đỉnh
Trục đối xứng
Giao với Oy tại A(0;-1), lấy điểm B(2;-1) đối xứng với A qua trục đối xứng
Lấy điểm C(-1;2) và D(3;2) thuộc đồ thị.