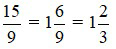Với giải bài tập Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương chi tiết bám sát nội dung sgk Toán 6 Tập 2 Kết nối tri thức với cuộc sống giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập môn Toán 6. Mời các bạn đón xem:
Giải bài tập Toán lớp 6 Bài 24: So sánh phân số. Hỗn số dương
Video giải Toán 6 Bài 24: So sánh phân số. Hỗn số dương - Kết nối tri thức
Mở đầu
Bài toán mở đầu trang 9 Toán lớp 6 Tập 2: Sau bài học này sẽ giúp chúng ta so sánh hai phân số trên.
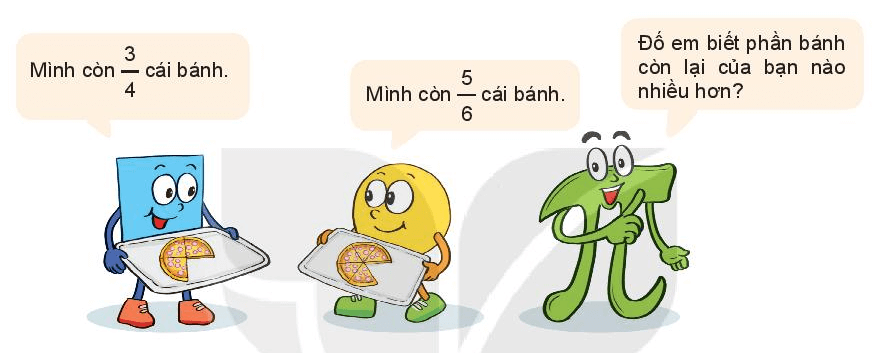
Lời giải:
Trong tình huống trên ta cần so sánh hai phân số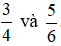 
Sau bài học này sẽ giúp chúng ta so sánh hai phân số trên.
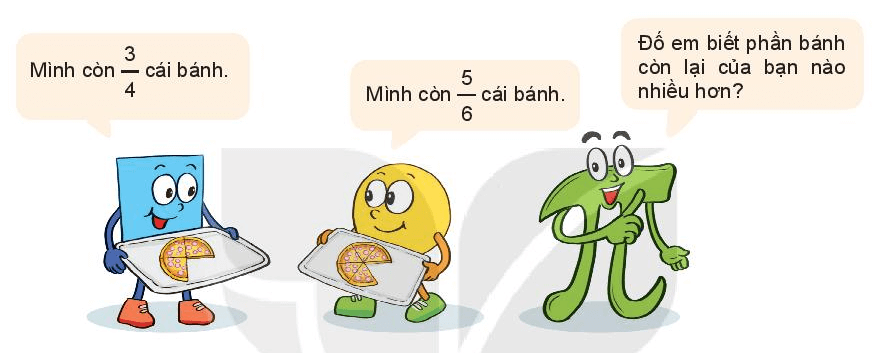
Trả lời câu hỏi giữa bài
Hoạt động 1 trang 9 Toán lớp 6 Tập 2: Em thực hiện các yêu cầu sau để quy đồng mẫu hai phân số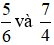 
Lời giải:
+) Phân tích các số 6 và 4 ra thừa số nguyên tố, ta được:
6 = 2. 3; 4 = 22
+) Ta thấy thừa số chung là 2; thừa số riêng là 3
+) Số mũ lớn nhất của 2 là 2, số mũ lớn nhất của 3 là 1
Khi đó BCNN(6; 4) = 23.3=12
Ta chọn mẫu chung của hai phân số là 12.
Hoạt động 2 trang 9 Toán lớp 6 Tập 2: Tương tự HĐ1, em hãy quy đồng mẫu hai phân số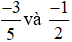 
Lời giải:
+) Phân tích các số 5 và 2 ra thừa số nguyên tố, ta được:
5 = 5 ; 2 = 2
+) Ta thấy không có thừa số chung; thừa số riêng là 2 và 5
+) Số mũ lớn nhất của 2 là 1, số mũ lớn nhất của 5 là 1
Khi đó BCNN(5, 2) = 2. 5 = 10
Ta chọn mẫu chung của hai phân số là 10.
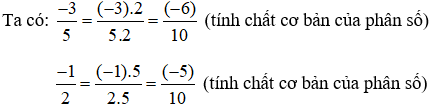
Luyện Tập 1 trang 10 Toán lớp 6 Tập 2: Quy đồng mẫu các phân số: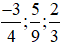 
Lời giải:
+) Ta có: 4 = 22 ; 9 = 32 ; 3 = 3. Do đó BCNN(4; 9; 3) = 22.32 =4.9 =36
+) Tìm thừa số phụ: 36: 4 = 9; 36: 9 = 4 và 36: 3 = 12
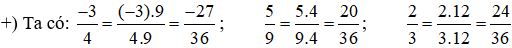
Lời giải:
+) Quy tắc so sánh hai phân số có cùng mẫu (tử và mẫu đều dương) thì phân số nào có tử lớn hơn thì phân số đó lớn hơn.
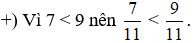
Luyện Tập 2 trang 10 Toán lớp 6 Tập 2: Tìm dấu thích hợp (>, <) thay cho dấu "?".
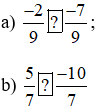, <) thay cho dấu "?"." />
Lời giải:
a) Hai phân số đã cho có chung mẫu nên ta chỉ cần so sánh tử số với nhau:
Vì 2 < 7 nên -2 > - 7
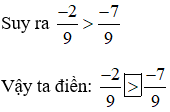, <) thay cho dấu "?"." />
b) Hai phân số này có chung mẫu nên để so sánh thì ta chỉ cần so sánh tử số với nhau:
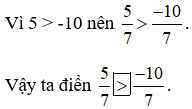, <) thay cho dấu "?"." />
Hoạt động 4 trang 10 Toán lớp 6 Tập 2: Tình huống mở đầu:
Đề giải quyết tình huống mở đầu, ta cần so sánh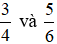 
. Em hãy thực hiện các yêu cầu sau:
Lời giải:
Ta có: 4 = 22; 6 = 2. 3
Do đó BCNN(4; 6) =22.3=4.3=12
+) Thừa số phụ: 12: 4 = 3; 12: 6 = 2
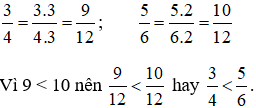
Vậy phần bánh còn lại của Tròn nhiều hơn phần bánh còn lại của Vuông.
Luyện Tập 3 trang 11 Toán lớp 6 Tập 2: So sánh các phân số sau:
Lời giải:
a) Ta có: 10 = 2. 5; 15 = 3. 5
Khi đó BCNN(10; 15) = 2. 3. 5 = 30
Thừa số phụ: 30: 10 = 3; 30: 15 = 2
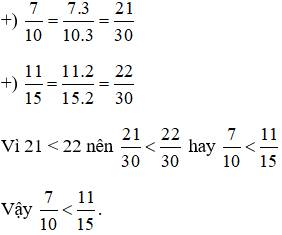
b) Ta có nên BCNN(8; 24) = 24
Thừa số phụ: 24: 8 = 3; 24: 24 = 1
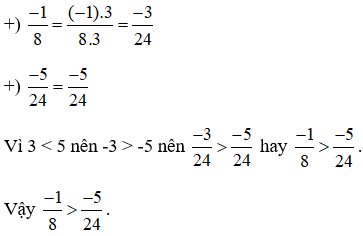
Thử thách nhỏ trang 11 Toán lớp 6 Tập 2: Không quy đồng mẫu số, em hãy so sánh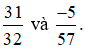 
Lời giải:
Hoạt động 5 trang 11 Toán lớp 6 Tập 2: Viết phân số biểu thị phần bánh của mỗi bạn.
Lời giải:
Chia đều ba cái bánh cho hai bạn thì mỗi bạn được số phần bánh là:
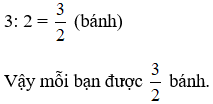
Lời giải:
Em đồng ý với Tròn vì có ba cái bánh, mỗi bạn được 1 cái bánh thì còn 1 cái bánh, chia đều cho 2 bạn thì mỗi bạn được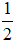 
cái bánh nữa.
Vậy Tròn nói mỗi bạn được 1 cái bánh và 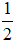cái bánh là đúng.
Câu hỏi trang 12 Toán lớp 6 Tập 2: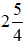 
có là một hỗn số không? Vì sao?
Lời giải:
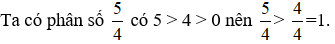
Vậy 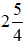không là một hỗn số vì phần phân số lớn hơn 1.
Bài tập
Bài 6.8 trang 12 Toán lớp 6 Tập 2: Quy đồng mẫu các phân số sau:
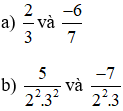
Lời giải:
a)
Tìm mẫu chung: BCNN(3, 7) = 3. 7 = 21
Tìm thừa số phụ: 21: 3 = 7; 21: 7 = 3
Ta có:
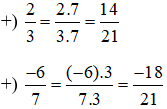
b)
Tìm mẫu chung: BCNN(22.32; 22.3) =22.32 = 4. 9 = 36
Tìm thừa số phụ: 36: (22.32) = 36: 36 = 1; 36: 22.3 = 36: 12 = 3
Ta có:
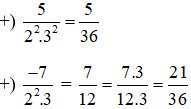
Bài 6.9 trang 12 Toán lớp 6 Tập 2: So sánh các phân số sau:
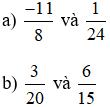
Lời giải:
a)
Cách 1: Vì nên BCNN(8; 24) = 24. Suy ra MTC = 24.
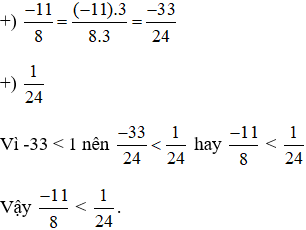
Cách 2:
b) Ta có 20 =22.5 ; 15=3.5
Ta chọn mẫu chung là BCNN(20; 15) =22.3.5=60
Tìm thừa số phụ: 60: 20 = 3; 60: 15 = 4
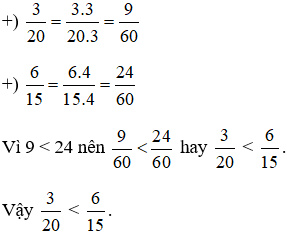
Lời giải:
Vì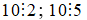 
nên BCNN(5; 10; 2) = 10
Suy ra MTC = 10.
Tìm thừa số phụ 10: 5 = 2; 10: 2 = 5
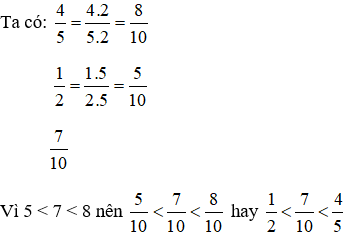
do đó môn bóng bàn là môn thể thao được học sinh lớp 6A yêu thích nhất.
Vậy môn bóng bàn là môn thể thao được học sinh lớp 6A yêu thích nhất.
Bài 6.11 trang 12 Toán lớp 6 Tập 2:
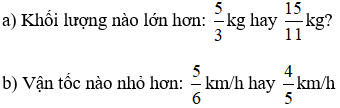
Lời giải:
a)
Tìm mẫu chung: BCNN(3; 11) = 33
Tìm thừa số phụ: 33: 3 = 11; 33: 11 = 3
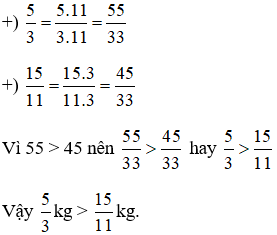
b)
Tìm mẫu chung: BCNN(6; 5) = 30
Tìm thừa số phụ: 30: 6 = 5; 30: 5 = 6
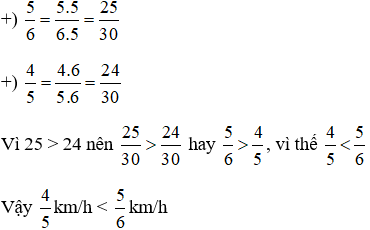
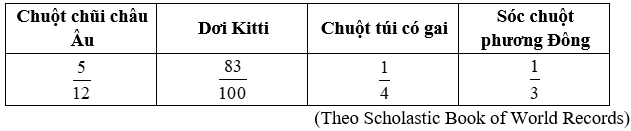
Hãy sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé.
Lời giải:
Ta có: 12 = 22.3; 100 = 22.52 ; 4 = 22; 3 = 3
Tìm mẫu chung: BCNN(12, 100, 4, 3) =52.22.3=300
Tìm thừa số phụ: 300: 12 = 25; 300: 100 = 3; 300: 4 = 75; 300: 3 = 100
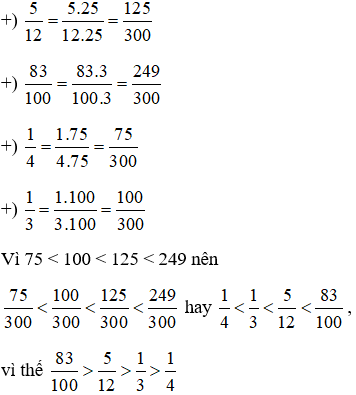
Do đó sắp xếp các động vật trên theo thứ tự chiều dài từ lớn đến bé: Dơi Kitti; Chuột chũi châu Âu, Sóc chuột phương Đông, Chuột túi có gai.
Lời giải:
Bài giảng Toán 6 Bài 24: So sánh phân số. Hỗn số dương - Kết nối tri thức
Xem thêm các bài giải SGK Toán lớp 6 Kết nối tri thức hay, chi tiết khác:
Bài 23: Mở rộng phân số. Phân số bằng nhau
Bài 25: Phép cộng và phép trừ phân số
Bài 26: Phép nhân và phép chia phân số
Lý thuyết So sánh phân số. Hỗn số dương
1. Quy đồng mẫu nhiều phân số
Để quy đồng hai hay nhiều phân số ta làm như sau:
Bước 1: Tìm một bội chung (thường là BCNN) của các mẫu để làm mẫu chung.
Bước 2: Tìm thừa số phụ của mỗi mẫu bằng cách chia mẫu chung cho từng mẫu.
Bước 3: Nhân tử và mẫu của mỗi phân số với thừa số phụ tương ứng.
Ví dụ 1: Để quy đồng ba phân số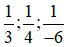 
ta làm như sau:
+ Đưa về các phân số có mẫu dương: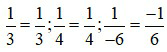 
.
+ Tìm mẫu chung: BCNN (3; 4; 6) = 12
+ Thừa số phụ:
12 : 3 = 4
12 : 4 = 3
12 : 6 = 2
Ta có:
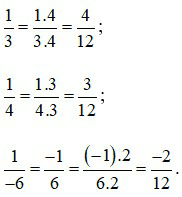
2. So sánh hai phân số
a) So sánh hai phân số cùng mẫu
– Trong hai phân số cùng một mẫu dương, phân số nào có tử lớn hơn thì phân số đó lớn hơn.
Ví dụ 2: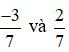 
là hai phân số có cùng mẫu số dương.
Vì –3 < 2 nên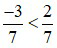 
.
b) So sánh hai phân số không cùng mẫu
– Muốn so sánh hai phân số không cùng mẫu, ta viết chúng dưới dạng hai phân số có cùng một mẫu dương rồi so sánh các tử số với nhau: phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
Ví dụ 3: So sánh hai phân số sau: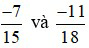 
.
BCNN (15; 18) = 90
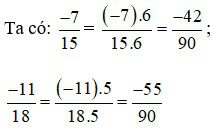
Vì –42 > –55 nên 
do đó,
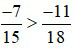
3. Hỗn số dương
– Khái niệm hỗn số dương: Với a, b, c là những số nguyên dương, ta gọi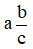 
là một hỗn số dương với a là phần nguyên và 
là phần phân số.
Ví dụ 4:
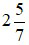là một hỗn số dương với phần nguyên là 2 và phần phân số là 
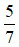. Khi đó ta đọc 
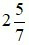là hai năm phần bảy.
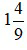là một hỗn số dương với phần nguyên là 1 và phần phân số là 
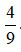. Khi đó ta đọc
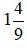là một bốn phần chín.
– Muốn đổi từ hỗn số sang phân số ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số.
Bước 2: Phần tử số mới sẽ bằng phần mẫu số nhân với phần nguyên và cộng với phần tử số ban đầu.
Ví dụ 5: Đổi hỗn số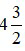 
sang phân số:
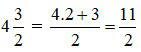
– Muốn đổi từ phân số sang hỗn số (điều kiện tử số của phân số phải lớn hơn mẫu số) ta làm như sau:
Bước 1: Giữ nguyên phần mẫu số và mẫu số này sẽ là mẫu số trong phần hỗn số mới.
Bước 2: Lấy phần tử số chia cho mẫu số, phần thương sẽ là phần nguyên trong hỗn số mới và phần dư là tử số mới của hỗn số.
Ví dụ 6: Đổi phân số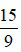 
sang hỗn số
Ta có 15 chia 9 được thương là 1 và dư 6 do đó:
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
