Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Tuyển tập đề thi học sinh giỏi toán lớp 8, tài liệu bao gồm 47 trang, tuyển chọn Đề thi học sinh giỏi toán lớp 8 (có đáp án và lời giải chi tiết – nếu có), giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.
Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:
ĐỀ THI SỐ 1
Câu 1: (4,0 điểm)
Phân tích các đa thức sau thành nhân tử :
Câu 2: (5,0 điểm)
Cho biểu thức :
Câu 3: (5,0 điểm)
a) Tìm x,y,z thỏa mãn phương trình sau :
9x2 + y2 + 2z2 – 18x + 4z - 6y + 20 = 0.
b) Cho và . Chứng minh rằng : .
Câu 4: (6,0 điểm)
Cho hình bình hành ABCD có đường chéo AC lớn hơn đường chéo BD. Gọi E, F lần lượt là hình chiếu của B và D xuống đường thẳng AC. Gọi H và K lần lượt là hình chiếu của C xuống đường thẳng AB và AD.
ĐỀ SỐ 2
Câu1.
a) Phân tích các đa thức sau ra thừa số:
b) Giải phương trình:
c) Cho . Chứng minh rằng:
Câu2. Cho biểu thức:
a. Rút gọn biểu thức A.
b. Tính giá trị của A , Biết |x| =.
c. Tìm giá trị của x để A < 0.
d. Tìm các giá trị nguyên của x để A có giá trị nguyên.
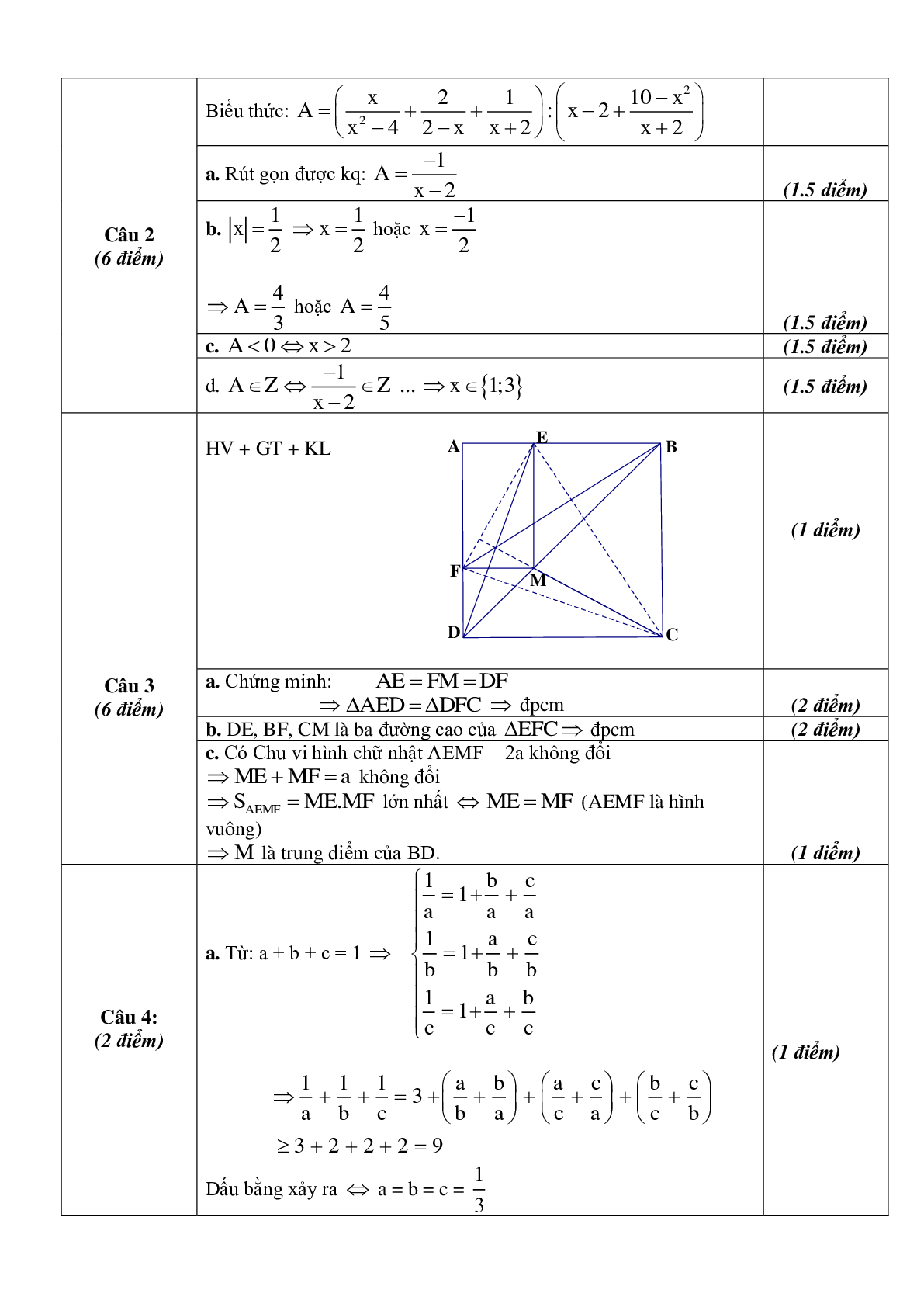
Câu 3. Cho hình vuông ABCD, M là một điểm tuỳ ý trên đường chéo BD. Kẻ MEAB, MFAD.
a. Chứng minh: DE=CF
b. Chứng minh ba đường thẳng: DE, BF, CM đồng quy.
c. Xác định vị trí của điểm M để diện tích tứ giác AEMF lớn nhất.
Câu 4.
a. Cho 3 số dương a, b, c có tổng bằng 1. Chứng minh rằng:
b. Cho a, b dương và
a2000 + b2000 = a2001 + b2001 = a2002 + b2002
Tinh: a2011 + b2011