Tailieumoi.vn xin giới thiệu đến các quý thầy cô, các em học sinh đang trong quá trình ôn tập tài liệu Bất biến trong các bài toán tổ hợp - Toán 11, tài liệu bao gồm 13 trang, đầy đủ lý thuyết, phương pháp giải chi tiết và bài tập có đáp án, giúp các em học sinh có thêm tài liệu tham khảo trong quá trình ôn tập, củng cố kiến thức và chuẩn bị cho bài thi môn Toán sắp tới. Chúc các em học sinh ôn tập thật hiệu quả và đạt được kết quả như mong đợi.

Mời các quý thầy cô và các em học sinh cùng tham khảo và tải về chi tiết tài liệu dưới đây:

BẤT BIẾN TRONG CÁC BÀI TOÁN TỔ HỢP 

Chúng ta có thể bắt đầu bằng bài toán dân gian sau:

Một người nông dân trồng được một cây khế thần có 99 quả chưa chín màu xanh và 100 quả đã chín màu vàng. Một con Quạ đến ăn mỗi ngày hai quả khế và nói với người nông dân: “ Ăn một quả trả một cục vàng, may túi ba gang mang đi mà đựng”. Quạ đến ăn hai quả khế bất kì và không phân biệt quả xanh hay quả vàng. Nếu Quạ ăn một quả xanh và một quả vàng thì cây khế lại sinh một quả xanh. Nếu Quạ ăn hai quả vàng hoặc hai quả xanh thì cây khế đều sinh ra một quả vàng. Hỏi có thể xảy ra trường hợp quả khế còn lại trên cây là quả màu vàng không?

Giải.

Ta kí hiệu:

Quả khế xanh là X; quả khế vàng là V; Quạ ăn quả là +; cây khế sinh ra quả là =. Khi đó, bài toán được rút gọn như sau

          X + X = V

          V + V = V

          V + X = X

          X + V = X

Ta thấy số lượng quả xanh hoặc không đổi hoặc giảm đi 2 sau mỗi lần Quạ ăn.

Vì trên cây số quả màu xanh là lẻ và số quả màu vàng là chẵn nên quả cuối cùng trên cây là quả xanh.

Câu hỏi được đặt ra là tính bất biến trong bài toán là gì?

Đó chính là số quả xanh dù quạ có ăn như thế nào đi nữa thì nó hoặc không thay đổi hoặc nếu nó thay đổi thì thay đổi một cách cố định là giảm đi hai quả.

Bài 1.   

Trên bảng, người ta viết các số tự nhiên lẻ liên tiếp từ 1 đến 2013, sau đó thực hiện trò chơi như sau: mỗi lần xóa hai số bất kì và viết vào bảng một số mới bằng tổng hai số đã xóa. Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại một số. Hỏi số cuối cùng còn lại trên bảng là bao nhiêu?

Giải.

Vì mỗi lần chơi ta thay hai số bằng tổng của chúng nên tổng các số trên bảng không thay đổi trong mọi thời điểm.

Tổng các số lúc đầu là

\(1 + 3 + 5 + ... + 2013 = 1014049\) nên ta được số cuối cùng là 1014049.

Ta nhận thấy bất biến của bài toán trên là tổng các số trên bảng không đổi trong mọi thời điểm.

Bài 2.   

Trên bảng, người ta viết các số tự nhiên liên tiếp từ 1 đến 2012, sau đó thực hiện trò chơi như sau: mỗi lần xóa hai số bất kì và viết vào bảng một số mới bằng hoặc hiệu hai số đã xóa (lấy số lớn trừ số nhỏ). Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại một số. Hỏi số cuối cùng còn lại trên bảng có thể là số 1 không?

Giải.

Cách 1.

Vì mỗi lần chơi số các số lẻ là không đổi hoặc giảm đi 2.

          lẻ      \( \pm \) lẻ     \( \to \) chẵn

          chẵn \( \pm \) chẵn \( \to \) chẵn

          lẻ      \( \pm \) chẵn \( \to \) lẻ

          chẵn \( \pm \) lẻ      \( \to \) lẻ

Lúc đầu có 1006 số lẻ nên số còn lại cuối cùng trên bảng phải là số lẻ. Do đó số còn lại không thể là số 2.

Bất biến của bài toán là số lượng số lẻ giảm đi 2 hoặc không đổi sau mỗi lần chơi.

Cách 2.

Xoá hai số \(a,b\) và thay bằng hiệu \(a - b\) thì tổng các số trên bảng giảm đi một đại lượng là \(a + b - (a - b) = 2b\) là một số chẵn.

Tổng các số lúc đầu là một số chẵn \(\left( {1 + 2 + ... + 2012 = 2025078} \right)\)nên suy ra số còn lại cuối cùng trên bảng cũng là một số chẵn.

Bất biến của bài toán là tổng các số trên bảng luôn giảm đi một đại lượng chẵn.

Bài 3.   

Trên bảng, người ta viết 1000 chữ số 1 và 20 chữ số 3, sau đó thực hiện trò chơi như sau: mỗi lần xóa hai số bất kì và viết vào bảng một số mới bằng tích hai số đã xóa. Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại một số. Hỏi số cuối cùng còn lại trên bảng có thể là bao nhiêu?

Giải.

Vì mỗi lần thực hiện trò chơi, ta thay 2 số bằng tích của chúng nên tích các số trên bảng không đổi trong mọi thời điểm. Tích các số lúc đầu là \({1^{1000}} \times {3^{20}} = 59049\) nên số còn lại trên bảng là \(59049\).

Bất biến của bài toán là tích các số trên bảng không thay đổi trong mọi thời điểm.

Bài 4.   

Trên bảng, người ta viết các số tự nhiên liên tiếp từ 1 đến 100, sau đó thực hiện trò chơi như sau: mỗi lần xóa hai số bất kì và viết vào bảng một số mới bằng tổng lập phương của hai số đã xóa. Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại một số. Hỏi số cuối cùng còn lại trên bảng có thể là số \({20132013^{2012}}\)không? Tại sao?

Giải.

Cách 1.

Tương tự như bài 2.

Bất biến là số lượng số lẻ hoặc giảm đi 2 hoặc không đổi sau mỗi lần thực hiện.

Cách 2.

Nếu thay hai số \(a,b\) bằng \({a^3} + {b^3}\) thì tổng các số trên bảng tăng một đại lượng

\({a^3} + {b^3} - (a + b) = ({a^3} - a) + ({b^3} - b) = (a - 1)a(a + 1) + (b - 1)b(b + 1)\) là một số chia hết cho 3, nên tổng các số trên bảng luôn kém nhau bội số của 3,

Tổng các số lúc đầu là 5050 chia 3 dư 1 nên số còn lại cuối cùng trên bảng phải là số chia 3 dư 1.

Như vậy số còn lại cuối cùng trên bảng không thể là số \({20132013^{2012}}\).

Bất biến của bài toán là tổng các số trên bảng tại mỗi thời điểm hơn kém nhau bội số của 3.

Bài 5.   

Cho số tự nhiên có 8 chữ số 12456789. Từ số này người ta đổi vị trí các chữ số của nó. Hỏi có thể tạo được một số mới là số chính phương hay không?

Giải.

Khi ta thay đổi vị trí các chữ số của nó thì tổng các chữ số là không đổi.

\(1 + 2 + ... + 9 = 42\) là một số chia hết cho 3 nhưng không chia hết cho 9.

Suy ra số được tạo thành chia hết cho 3 nhưng không chia hết cho 9 nên không thể là số chính phương.

Bất biến của bài toán là tổng các chữ số tạo thành luôn không đổi.

Bài 6.   

Trên bảng, người ta viết 20 dấu cộng và 27 dấu trừ tại các vị trí bất kì, sau đó thực hiện trò chơi như sau: mỗi lần xóa hai dấu bất kì và viết vào bảng một dấu cộng nếu xóa hai dấu giống nhau và dấu trừ nếu xóa hai dấu khác nhau. Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại một dấu. Hỏi dấu cuối cùng còn lại trên bảng có thể là dấu gì?

Giải.

Cách 1.

Như bài 2.

Bất biến là số dấu trừ hoặc không đổi hoặc giảm đi 2 sau mỗi lần thực hiện.

Cách 2.

Ta thay mỗi dấu cộng bằng số 1, dấu trừ bằng số \( - \)1, thao tác thực hiện xoá 2 số và viết lại 1 số thì số viết lại là tích của chúng.

          \(\begin{array}{l}1\,\,\,\,\,\,\,\, \times \,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\,1\\ - 1\,\,\,\, \times \,\,\, - \,1\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\,1\\ - 1\,\,\,\, \times \,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\, = \,\,\,\, - 1\\1\,\,\,\,\,\,\,\, \times \,\,\, - \,1\,\,\,\,\,\,\,\,\, = \,\,\,\, - 1\end{array}\)

Giả thiết cho tích các số trên bảng bằng \( - \)1 nên số cuối cùng còn lại trên bảng là số \( - \)1, nghĩa là trên bảng còn lại dấu trừ.

Bất biến là tính  không đổi của tích các số trên bảng.

Cách 3.

 Thay dấu + bằng số 0, dấu \( - \) bằng số 1. Thao tác thực hiện là tổng của 2 số xoá đi, nếu tổng là số chẵn thì ta viết lại số 0, tổng là số lẻ thì ta viết lại số 1.

\(\begin{array}{l}0\,\,\,\,\,\,\, + \,\,\,\,\,\,0\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,\,0\\1\,\,\,\,\,\,\,\, + \,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,0\\0\,\,\,\,\,\,\, + \,\,\,\,\,\,\,1\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,1\\1\,\,\,\,\,\,\,\, + \,\,\,\,\,\,0\,\,\,\,\,\,\,\,\, = \,\,\,\,\,\,\,1\end{array}\)

Như vậy tổng các số trên bảng là 1 số lẻ (bằng 27) thì số cuối cùng trên bảng là 1 số lẻ. Vậy trên bảng còn lại dấu trừ.

Bất biến là tính không đổi của tổng các số chẵn.

Bài 7.   

Trên bảng, người ta viết 3 số nguyên, sau đó thực hiện trò chơi như sau: mỗi lần xóa một số bất kì và viết vào bảng tổng của hai số còn lại trừ đi 1. Cứ tiếp tục trò chơi cho đến khi trên bảng còn lại ba số 17; 1967; 1983. Hỏi ba số đầu tiên trên bảng có thể là ba số 2, 2, 2 không?

Giải.

Giả sử ba số đầu tiên viết trên bảng là 2, 2, 2.

Sau bước đầu tiên ta nhận được ba số là 2, 2, 3, trong đó có 2 số chẵn và 1 số lẻ.

Từ bước thứ hai trở đi, lúc nào kết quả cũng luôn có hai số chẵn và một số lẻ. (Những số chẵn bằng tổng của 1 số chẵn và 1 số lẻ trừ đi 1; số lẻ là tổng của hai số chẵn trừ đi 1).

Nhưng trong kết quả đều là 3 số lẻ nên 3 số đầu tiên không thể là 2, 2, 2.

Bất biến là tính chẵn, lẻ của ba số không thay đổi.

Bài 8.   

Trên bảng cho 3 số 2, 2, 2. Ta xoá đi một trong 3 số và thay vào đó tổng của hai số còn lại trừ đi 1. Hỏi sau 1 số lần thực hiện ta có thể thu được các số 11; 1; 2011 được hay không?

Bài 9.   

Có 2005 đồng xu, mỗi đồng xu có hai mặt, một mặt màu xanh và một mặt màu đỏ. Xếp các đồng xu trên bảng sao cho các mặt màu xanh ngửa lên. Thực hiện trò chơi như sau: Mỗi lần thực hiện, cho phép đổi bốn mặt của bốn đồng xu tùy ý. Hỏi có thể nhận được kết quả mà tất cả các đồng xu đều có mặt đỏ ngửa lên trên hay không?

Giải.

Thay mỗi đồng xu mặt màu xanh ngửa lên trên bởi số \(\left( { - 1} \right)\). Thay mỗi đồng xu mặt màu đỏ ngửa lên trên bởi số \(\left( { + 1} \right)\). Khi đó, mỗi cách thực hiện theo đề bài có thể mô tả dưới dạng khác như sau

Bốn số bất kì được xoá đi và thay mỗi số bằng số đối của nó. Ban đầu có 2005 số \(\left( { - 1} \right)\) tương ứng với 2005 đồng xu mặt màu xanh ngửa lên trên. Ta thấy rằng nếu thay 4 số \(a,\,\,b,\,\,c,\,\,d\) bởi 4 số \( - a,\, - \,b,\, - \,c,\, - \,d\) thì tích các số mới thay vào là \(\left( { - a} \right)\left( { - \,b} \right)\left( {\, - \,c} \right)\left( { - \,d} \right) = abcd\) bằng tích các số ban đầu.

Như vậy, tại mọi thời điểm thì tích của các số không đổi. Ban đầu có 2005 số \(\left( { - 1} \right)\) nên tích của chúng là \(\left( { - 1} \right)\).

Suy ra tại mọi thời điểm thì tích số luôn là \(\left( { - 1} \right)\). Vậy không nhận được kết quả mà tất cả các đồng xu đều có mặt đỏ ngửa lên trên.

Bất biến là tích số không đổi trong mọi thời điểm.

Bài 10.                  

Ngoài biển Đông, trên một hòn đảo giống con tắc kè sinh sống có ba loại màu: màu xám có 133 con, màu nâu có 155 con, màu đỏ có 177 con. Nếu hai con tắc kè khác màu gặp nhau thì chúng đồng thời đổi sang màu thứ ba. Trong trường hợp hai con tắc kè cùng màu gặp nhau thì chúng giữ nguyên không đổi màu. Hỏi có thể  ra tình trạng là trên đảo tất cả con tắc kè trở thành cùng một màu được không?

Nhận xét.

·      Giả sử con tắc kè đỏ và con tắc kè nâu gặp nhau thì chúng đổi màu xám. Khi đó, ta có 135 con tắc kè xám, 154 con tắc kè nâu, 176 con tắc kè đỏ. Số dư của 135; 154; 176 cho 3 lần lượt là 0; 1; 2.

·      Giả sử con tắc kè đỏ và con tắc kè xám gặp nhau thì chúng đổi màu nâu. Khi đó, ta có 132 con tắc kè xám, 157 con tắc kè nâu, 176 con tắc kè đỏ. Số dư của 132; 157; 176 cho 3 lần lượt là 0; 1; 2.

·      Giả sử con tắc kè xám và con tắc kè nâu gặp nhau thì chúng đổi màu đỏ. Khi đó, ta có 132 con tắc kè xám, 154 con tắc kè nâu, 179 con tắc kè đỏ. Số dư của 132; 154; 179 cho 3 lần lượt là 0; 1; 2.

Bất biến là dù thay đổi màu như thế nào thì số dư của các số lượng tắc kè chia cho 3 đều có đầy đủ 0; 1; 2.

Nếu tất cả tắc kè có cùng một màu thì số dư của số lượng tắc kè là 0; 0; 0 và điều này là vô lí.

Như vậy không thể xảy ra tình trạng trên đảo mà tất cả tắc kè đều đổi thành một màu.

Giải.

Mỗi trạng thái trên đảo gồm a con tắc kè xanh, b con tắc kè đỏ và c con tắc kè nâu với \(a + b + c = 465\).

Phép biến đổi màu sẽ chuyển từ trạng thái \(\left( {a;b;c} \right)\) sang một trong ba trạng thái \(\left( {a - 1;b - 1;c + 2} \right)\)hoặc \(\left( {a - 1;b + 2;c - 1} \right)\)hoặc \(\left( {a + 2;b - 1;c - 1} \right)\).

Ta thấy \(\left( {a - 1} \right) - \left( {b - 1} \right) \equiv \left( {a - 1} \right) - \left( {b + 2} \right) \equiv \left( {a + 2} \right) - \left( {b - 1} \right) \equiv a - b\,\,\,\left( {\bmod \,3} \right)\).

Bất biến \(X\) là sai khác giữa tắc kè xám và số tắc kè đỏ theo modulo 3. Lúc đầu \(X \equiv 2\,\,(\bmod \,3)\) và khi tất cả các tắc kè cùng màu thì \(X \equiv 0\,\,(\bmod \,3)\). Vì vậy, không thể xảy ra các con tắc kè có cùng màu.

Bài 11.                  

Có 1981 tách trà đặt trên 1 bàn. Lúc đầu tất cả các tách đều được đặt ngửa lên. Giả sử mỗi lần, người ta làm cho 200 tách trong chúng lật ngược lại. Hỏi sau một số lần như vậy, có thể làm cho tất cả các tách đều úp xuống được không?

Bất biến là số tách đang úp luôn thay đổi 1 lượng chẵn.

Bài 12.                  

Trong dãy 1, 9, 9, 8,…mỗi chữ số bắt đầu từ chữ số thứ năm bằng chữ số hàng đơn vị của tổng 4 chữ số liền trước nó. Hỏi trong dãy này có gặp các bộ 1234 và 5687 không?

Bất biến là sau 4 số lẻ có 1 số chẵn và sau số chẵn đó là 4 số lẻ.

Bài 13.                  

Cho n là 1 số nguyên dương lẻ. Người ta viết các số 1, 2, 3,…,2n trên bảng. Sau đó, người ta lấy hai số bất kì a, b thuộc dãy trên, xóa chúng đi và viết vào đó

 |a – b|. Chứng minh sau một số lần thực hiện như vậy thì số còn lại trên bảng cuối cùng là số lẻ.

Bất biến là tính chẵn lẻ của tổng các số trên bảng.

Bài 14.                  

Hai người chơi cờ, mỗi ván người thắng được hai điểm, người thua được 0 điểm. Nếu trận hòa thì mỗi người được một điểm. Hỏi sau một số ván cờ có thể xảy ra trường hợp một người được 9 điểm, người kia được 10 điểm không?

Tính chẵn, lẻ của tổng điểm hai người chơi.

Bài 15.                  

Một tờ giấy được xé thành 5 mảnh, một số trong số 5 mảnh nhỏ này được xé thành 5 mảnh nhỏ nữa và một số trong các mảnh nhỏ này được xé thành 5 mảnh… Vậy nếu cứ tiếp tục xé như vậy thì có khi nào ta được 2002 mảnh giấy hay không? Được 2005 mảnh giấy hay không?

Bất biến là số mảnh giấy sau mỗi lần xé có dạng 4k + 1.

Bài 16.                  

Có 3 đống sỏi gồm những viên sỏi nhỏ có số lượng tương ứng là 19; 8; 9 viên sỏi. Ta được phép chọn 2 đống sỏi và chuyển 1 viên sỏi của những đống sỏi đã chọn sang đống sỏi thứ ba. Sau 1 số lần làm như vậy thì có khả năng tạo ra các đống sỏi đều có 12 viên sỏi hay không?

Bất biến theo modulo 3.

Bài 17.                  

Một bàn cờ vua 8 x 8. Chứng minh rằng nếu xuất phát từ 1 ô góc, con mã có thể đi qua tất cả các ô của bàn cờ, mỗi ô một lần và kết thúc ở ô góc đối diện với ô góc nó xuất phát.

Giải.

Mỗi lần đi, con mã sẽ chuyển sang 1 ô khác màu với ô mà nó đang đứng.

Vì thế nếu lúc đầu con mã đứng ở ô màu trắng thì sau 1 số lẻ nước đi, con mã sẽ chuyển sang ô màu đen và sau 1 số chẵn nước đi, con mã sẽ chuyển sang ô màu trắng. Và đây chính là bất biến của bài toán.

Nếu đi qua tất cả các ô của bàn cờ, mỗi lần 1 ô thì con mã phải đi hết 63 bước. Do đó ô mà nó kết thúc phải khác màu với ô ban đầu nó xuất phát. Và đó không thể là góc đối diện.

Bài 18.                  

Trên một bảng ô vuông có 8 x 8 ô vuông bao gồm 32 ô trắng và 32 ô đen. Nếu một người chơi có thể thay tất cả ô trắng thành ô đen và ô đen thành ô trắng cùng một lúc trong một hàng hay cột bất kì, thì có thể thực hiện được hữu hạn bước thay đổi như vậy để trên bảng chỉ còn đúng một ô đen hay không?

Giải.

Nếu có đúng k ô đen trong 1 hàng hoặc 1 cột trước khi thực hiện trò chơi, thì sau khi chơi 1 lần, số ô đen trong hàng đó hoặc cột đó sẽ là \(8 - k\). Do đó sự thay đổi số ô đen là \(\left( {8 - k} \right) - k = 8 - 2k\)và là một số chẵn. Do bắt đầu có 32 ô đen nên không thể chỉ còn lại 1 ô đen trên bảng tại 1 bước biến đổi nào đó.

Bài 19.                  

Tại mỗi ô vuông trong bảng 8 x 8 được viết một số nguyên. Ta có thể chọn bất kì bảng nhỏ 3 x 3 hoặc 4 x 4 và tăng tất cả số trong bảng nhỏ lên 1. Với cách làm như vậy liệu có thể nhận được những số chia hết cho 3 trong tất cả ô vuông của bảng \(8 \times 8\)  sau một số hữu hạn lần thực hiện không?

Giải.

Mỗi hình vuông cỡ \(4 \times 4\)chứa 12 ô gạch chéo, còn mỗi hình vuông cỡ \(3 \times 3\)chứa 6 hoặc 9 ô gạch chéo. Như vậy sau một thao tác tổng các số trong các ô gạch chéo chia cho 3 có số dư không đổi. Vì thế ngay từ đầu tính được tổng không chia hết cho 3 thì trong các ô gạch chéo luôn luôn chứa những ô mà trong đó có chứa các số không phải là bội của 3. Vì vậy, không thể có nhận được kết quả như trên.

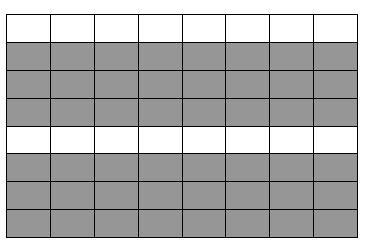
Bài 20.                  

Một nhóm học sinh được xếp thành 9 hàng, mỗi hàng có 9 người. Thực hiện trò chơi như sau: sau hiệu lệnh của người chỉ huy, mỗi người phải rời khỏi vị trí của mình và chuyển sang vị trí của người gần mình nhất nhưng không được chuyển sang vị trí của những người cùng hàng hoặc cùng cột với mình, hai người có thể cùng chuyển tới một vị trí. Chứng tỏ rằng sau hiệu lệnh của người chỉ huy có ít nhất 9 chỗ trống.

Giải.

Ta xem như mỗi học sinh đứng trong 1 ô của bảng ô vuông \(9 \times 9\). Tô màu như hình vẽ.

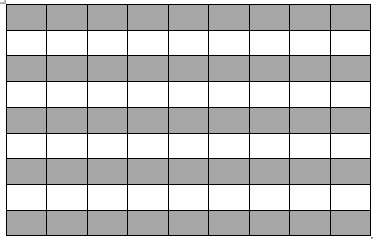
Sau hiệu lệnh của người chỉ huy, mỗi học sinh đều chuyển sang ô khác màu với ô học sinh đó đang đứng. Có tất cả 45 ô đen và 36 ô trắng nên sau hiệu lệnh của người chỉ huy có ít nhất 9 ô trống.

Bài 21.                  

Một hình tròn được chia thành 2014 hình quạt. Trong mỗi hình quạt có 1 viên bi. Thực hiện trò chơi sau: mỗi lần cho phép lấy ra 2 viên bi trong hai hình quạt nào đó và chuyển sang các ô bên cạnh nhưng theo hai chiều ngược nhau. Hỏi sau 1 số lần có thể chuyển hết các viên bi vào 1 hình quạt được không?

Giải.

Cách 1.

Ta tô màu xen kẽ các ô của hình quạt, như vậy có 1007 ô được tô màu và 1007 ô không được tô màu.

Ta có nhận xét:

Nếu di chuyển 1 bi ở ô màu và 1 bi ở ô trắng thì tổng số bi ở 1007 ô màu không đổi.

Nếu di chuyển bi ở 2 ô màu, mỗi ô 1 bi thì tổng số bi ở các ô màu sẽ giảm đi 2 (ô trắng tăng 2).

 Nếu di chuyển bi ở 2 ô trắng, mỗi ô 1 bi thì tổng số bi ở các ô màu sẽ tăng lên 2 (ô trắng giảm đi 2).

Như vậy, tổng số bi ở các ô màu hoặc không đổi hoặc tăng 2 hoặc giảm 2 tức là không thay đổi tính chẵn, lẻ. Ban đầu có 1007 ô màu nên sau hữu hạn lần di chuyển bi theo quy luật thì tổng số bi ơ 1007 ô màu luôn khác 0 và khác 2014. Do đó không thể di chuyển tất cả các viên bi về cùng 1 ô.

Cách 2.

Tô màu các hình quạt bởi 2 màu đen, trắng sao cho 2 hình quạt kề nhau thì khác  màu. Gọi S(n) và T(n) tương ứng là số viên bi trong các hình quạt màu đen và số viên bi trong các hình quạt màu trắng sau bước di chuyển thứ n.

Ta thấy tổng số viên bi trong các ô trắng hoặc đen tăng 2, giảm 2 hoặc không đổi. Khi đó S(n) và T(n) bất biến theo mod 2.

Do \(S\left( 0 \right) = T\left( 0 \right) = 1007\)nên S(n) và T(n) lẻ với mọi n. Do đó không thể có trạng thái mà tất cả các viên bi ở trong cùng 1 hình quạt.

Cách 3.

Đánh số các hình quạt từ 1 đến 2014. Đặt S bằng tổng số bi trong các ô chẵn trừ đi tổng số bi trong các ô lẻ. Ban đầu S = 0

Khi di chuyển 1 viên bi từ ô chẵn sang ô lẻ, S sẽ giảm đi 2, còn khi chuyển từ ô lẻ sang ô chẵn thì S sẽ tăng lên 2. Do đó sau mỗi lần chuyển chỗ 2 viên bi, S sẽ không đổi, hoặc giảm 4, hoặc tăng 4.

Như vậy, S luôn chia hết cho 4. Do đó không thể dồn tất cả các viên bi về 1 ô được.

Bài 22.                  

1 dãy gồm 9 ô vuông được đánh số thứ tự từ 1 đến 9, trong mỗi ô có 1 viên bi.

Thực hiện trò chơi như sau: mỗi lần lấy hai viên bi ở 2 ô vuông khác nhau rồi chuyển mỗi viên sang ô kề với ô chứa nó nhưng theo 2 chiều ngược nhau. Hỏi sau 1 số hữu hạn bước ta có thể nhận được kết quả là:

a)    Cả 9 viên bi đều nằm trong cùng 1 ô được không?

b)    Không có viên bi nào ở các ô mang số thứ tự lẻ hay không?

c)    Có 5 viên bi ở ô số 9 không?

Giải.

Mỗi viên bi ở ô nào thì ta gắn cho nó số thứ tự ở ô đó.

Gọi S(n) là tổng các số được gắn trên các viên bi sau bước chuyển thứ n.

Ta có S(n) là đại lượng bất biến.

Vậy S(n) = S(0) = 45

a)    S(n) = 45 nên nếu tất cả các viên bi đều nằm trong cùng 1 ô thì đó là ô số 5.

b)    Vì S(n) là số lẻ nên phải có ít nhất 1 viên bi mang số lẻ.

c)    Nếu có 5 viên bi ở ô số 9 thì 4 viên bi khác ở các ô còn lại nên S(n) > 45. Do đó không thể có trường hợp 5 viên bi ở ô số 9.

Bài 23.                  

Một dãy có 19 phòng. Ban đầu mỗi phòng có 1 người. Sau đó cứ mỗi ngày có 2 người nào đó cùng chuyển sang 2 phòng bên cạnh nhưng theo 2 chiều ngược nhau. Hỏi sau 1 số ngày có hay không trường hợp mà

a)    Không có ai ở phòng có số thứ tự chẵn.

b)    Có 10 người ở phòng cuối.

Bài 24.                  

Cho một bảng hình vuông có cạnh 10cm được chia thành 100 ô vuông nhỏ với cạnh 1 cm. Người ta đặt lên đó 25 hình chữ nhật như nhau có chiều cao 4cm và chiều rộng 1cm, mỗi hình chữ nhật được chia thành 4 ô vuông có cạnh 1cm. Hỏi có sắp những hình chữ nhật trên bảng hình vuông sao cho chúng phủ toàn bộ bảng hình vuông hay không? ( không chấp nhận hình chữ nhật nào lồi ra khỏi cạnh của hình vuông).

Bài 25.                  

Chứng minh rằng bảng hình vuông 10 x 10 không thể lát bằng các miếng như hình vẽ sau:

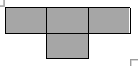
Bài 26.                  

Một cái sân hình chữ nhật được lát bằng các viên gạch hình chữ nhật kích thước 2 x 2 hoặc 1 x 4. Sau đó người ta bị mất 1 viên 2 x 2 và bổ sung thêm 1 viên 1 x 4. Hỏi có thể lát lại sân hay không?

Bài 27.                  

Một con rôbôt nhảy trong mặt phẳng tọa độ theo quy tắc sau: Xuất phát từ điểm (x, y), con rôbôt nhảy đến điểm (x’,y’) xác định như sau:

\(x' = \frac{{x + y}}{2};y' = \frac{{2xy}}{{x + y}}\) . Chứng minh rằng nếu ban đầu con rôbôt đứng ở điểm (2009;2010) thì không bao giờ con rôbôt nhảy vào được trong đường tròn (C) có tâm là gốc toạ độ O và bán kính R = 2840.

Bài 28.                  

Trên bảng cho đa thức \(f(x) = {x^2} + 4x + 3\). Thực hiện trò chơi sau, nếu trên bảng đã có đa thức \(P\left( x \right)\) thì được phép viết thêm lên bảng một trong hai đa thức sau

\(Q\left( x \right) = {x^2}f\left( {\frac{1}{x} + 1} \right),\,\,\,\,R\left( x \right) = {\left( {x - 1} \right)^2}f\left( {\frac{1}{{x - 1}}} \right)\)

Hỏi sau 1 số bước ta có thể viết được đa thức

\(g\left( x \right) = {x^2} + 10x + 9\)

hay không?

Bài 29.                  

Ở 6 đỉnh của 1 lục giác lồi có ghi 6 số chẵn liên tiếp theo chiều kim đồng hồ. Thực hiện trò chơi như sau, mỗi lần lấy ra 1 cạnh nào đó và cộng 2 số trên cạnh đó với cùng 1 số nguyên. Hỏi sau 1 số bước có thể nhận được kết quả là cả 6 số tại các đỉnh của lục giác đều bằng nhau được hay không?

Giải.

Giả sử 6 đỉnh của lục giác là A, B, C, D, E, F và các số viết tại các đỉnh đó ban đầu là a, a + 2, a + 4, a + 6, a + 8, a + 10.

Gọi S(n) là hiệu giữa tổng các số ở các đỉnh B, D, F và tổng các số ở các đỉnh A, C, E. Khi đó, S(n) là một đại lượng bất biến và S(n)  = S(0) = 6.

Mà theo đề bài, cả 6 số tại các đỉnh của lục giác đều bằng nhau, có nghĩa S(n) = 0 và điều này không thể xảy ra.

Bài 30.                  

Trên bảng ghi các số từ 1 đến 2005. Thực hiện trò chơi như sau, mỗi lần thay đồng thời tất cả các số có ở trên bảng bởi tổng các chữ số của nó. Hỏi nếu sau 1 số lần ta nhận được 2005 số mà mỗi số chỉ gồm 1 chữ số thì có bao nhiêu số 1.

Bài 31.                  

Mỗi số trong dãy \({2^1};{2^2};2{ & ^3};...;{2^{2005}}\) đều được thay bởi tổng các chữ số của nó. Tiếp tục làm như vậy với các số nhận được cho tới khi tất cả các số trong dãy đều có 1 chữ số. Chứng minh rằng trong dãy này số các số 2 nhiều hơn số các số 1.

Bài 32.                  

Hình vuông \(8 \times 8\) bỏ đi hai ô ở góc đối nhau. Có thể phủ phần còn lại bởi 31 quân đômino \(1 \times 2\) không?

Bất biến là hiệu số giữa số ô trắng và số ô đen trên bảng.

Bài 33.                  

   Một quân cờ được gọi là “quân lạc đà” có nghĩa là di chuyển sang ô kề và sau đó di chuyển ba ô theo hướng vuông góc với hướng vừa di chuyển. Quân mã di chuyển theo hướng (1; 2), quân lạc đà di chuyển theo hướng (1; 3). Hỏi liệu quân lạc đà có thể di chuyển từ 1 ô sang ô kề nó không trong bàn cờ \(10 \times 10\)?

Tô màu như bàn cờ. Bất biến là quân lạc đà luôn di chuyển trong các ô cùng màu và hai ô kề nhau là 2 ô khác màu.

Bài 34.                  

Một bảng hình chữ nhật có thể phủ kín không đè lên nhau bởi các hình \(1 \times 4\) và \(2 \times 2\). Khi bỏ các hình này ra ngoài, chúng ta làm mất một hình \(2 \times 2\) và thay vào đó một hình \(1 \times 4\). Liệu có thể dùng các hình lúc này phủ kín hình chữ nhật được không?

Bài 35.                  

Xung quanh một đường tròn ta viết 50 số theo thứ tự 1, 0, 1, 0, 0,…0. Cho phép tăng hai số viết liền nhau lên 1 đơn vị. Có thể nhận được dãy tất cả các số bằng nhau sau một số hữu hạn lần hay không?

Bài 36.                  

Xét một đa giác đều 12 đỉnh \({A_1},{A_2},...,{A_{12}}\). Tại đỉnh \({A_1}\) ta viết số \(\left( { - 1} \right)\), tại các đỉnh khác ta viết số \(\left( { + 1} \right)\). Mỗi phép biến đổi ta đổi dấu k đỉnh liền kề của đa giác. Hỏi có thể thu được trạng thái là đỉnh \({A_2}\) viết số \(\left( { - 1} \right)\) và các đỉnh còn lại viết số \(\left( { + 1} \right)\) sau một số hữu hạn phép biến đổi hay không?

a)    k = 6.

b)    k = 4.

c)    k = 3.

Bài 37.                  

 Mỗi số trong các số \({a_1},{a_2},...,{a_n}\) nhận một trong hai giá trị là 1 hoặc – 1. Biết rằng     

\(S = {a_1}{a_2}{a_3}{a_4} + {a_2}{a_3}{a_4}{a_5} + ... + {a_n}{a_1}{a_2}{a_3} = 0\). Chứng minh n chia hết cho 4.

Bất biến là S không thay đổi số dư khi chia cho 4 nếu ta đổi dấu của 4 số hạng liên tiếp.

Bài 38.                  

(VMO 2006) Xét bảng ô vuông \(m \times n\) (\(m,n\) là các số nguyên dương lớn hơn 3). Thực hiện trò chơi sau: mỗi lần đặt 4 viên bi vào 4 ô của bảng (mỗi ô 1 viên) mà 4 ô đó thành 1 trong các hình dưới đây:

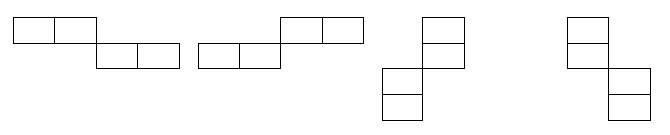
Hỏi sau 1 số lần ta có thể nhận được bảng mà số bi trong các ô bằng nhau được không nếu:

a)    \(m = 2004;n = 2006\)

b)    \(m = 2005;n = 2006\)

Bài 39.                  

Các số tự nhiên 0, 1, 2, 3,… được viết trong các ô của một bảng ô vuông kích thước \(2003 \times 2003\) theo vòng xoáy trôn ốc (xoay ngược kim đồng hồ) sao cho số 0 nằm ở ô trung tâm (tâm của bảng). Các dòng và cột của bảng được đánh số tăng dần từ dưới lên trên và từ trái sang phải ( bắt đầu từ số 1).

a)    Số 2004 nằm ở dòng nào, cột nào? Vì sao?

b)    Thực hiện phép toán sau: lần đầu tiên, ta thay số 0 ở ô trung tâm bởi số 1998; mỗi lần tiếp theo, cho phép lấy ra 12 số trong 12 ô liên tiếp trong cùng 1 hàng hoặc trong cùng 1 cột hoặc trong cùng 1 hình chữ nhật \(3 \times 4\) rồi tăng mỗi số đó lên 1 đơn vị. Hỏi sau một số lần như vậy ta có thể làm cho tất cả các số trong bảng đều là bội của 2004 hay không? Tại sao?

Bài 40.                  

Xác định các số nguyên dương m, n sao cho bảng \(m \times n\) có thể lát được bởi các quân hình chữ L dưới đây

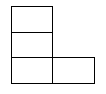
Bài 41.                  

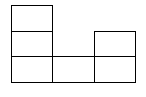
(IMO 2004) Ta định nghĩa viên gạch hình móc câu là hình gồm 6 ô vuông đơn vị như hình vẽ dưới đây hoặc hình nhận được do lật hình đó ( sang trái, sang phải, lên trên, xuống dưới) hoặc hình đó nhận được do xoay hình đó đi 1 góc.

Hãy xác định tất cả hình chữ nhật \(m \times n\), trong đó m, n là các số nguyên dương sao cho có thể lát hình chữ nhật đó bằng các viên gạch hình móc câu.

Bài 42.                  

(Corolado MO 1997) Mỗi ô của bảng \(1997 \times 1997\)điền các số (+1) hoặc \(\left( { - 1} \right)\). Mỗi hàng ta tính tích \({R_i}\) các số trong hàng đó. Mỗi cột ta tính tích \({C_i}\) các số trong cột đó. Chứng minh rằng \(\sum\limits_{i = 1}^{1997} {\left( {{R_i} + {C_i}} \right)} \) luôn khác không.

Bài 43.                  

(Hungary MO 1989) Mỗi đỉnh của 1 hình vuông đặt 1 viên sỏi. Thực hiện thay đổi số sỏi theo quy luật sau: ta có thể lấy đi 1 số sỏi ở 1 đỉnh và thêm vào một trong hai đỉnh kề bên một số sỏi gấp đôi. Hỏi có thể nhận được 1989; 1988; 1990; 1989 viên sỏi tại các đỉnh liên tiếp của hình vuông được hay không?

Bài 44.                  

(VMO 1992) Cho bảng hình chữ nhật \(1991 \times 1992\) với 1991 hàng và 1992 cột. Kí hiệu ô vuông nằm ở giao của hàng thứ m (kể từ trên xuống) và cột thứ n ( kể từ trái sang phải) là \(\left( {m,\,n} \right)\). Tô màu các ô vuông của bảng theo cách sau: lần thứ nhất tô 3 ô \(\left( {r,\,\,\,s} \right);\left( {r + 1,\,\,\,s + 1} \right);\left( {r + 2,\,\,\,s + 2} \right)\) với \(r;s\) là hai số tự nhiên cho trước thoả mãn \(1 \le r \le 1989;\,\,1 \le s \le 1991\), từ lần thứ hai mỗi lần tô đúng 3 ô chưa có màu nằm cạnh nhau hoặc trong cùng 1 hàng hoặc trong cùng 1 cột. Hỏi bằng cách đó có thể tô màu được tất cả các ô vuông của bảng đã cho hay không?

Bài 45.                  

(VMO 1993) Cho đa giác lồi \({A_1}{A_2}...{A_{1993}}\) mà tại mỗi đỉnh đã ghi 1 dấu cộng \(\left(  +  \right)\)  hoặc một dấu trừ \(\left(  -  \right)\) sao cho trong 1993 dấu đó có cả dấu \(\left(  +  \right)\) và \(\left(  -  \right)\).

Thực hiện quy tắc thay dấu như sau: mỗi lần, thay dấu đồng thời tại tất cả các đỉnh \({A_i}\left( {i = 1,2,...,1993} \right)\) của đa giác theo quy tắc:

·      Nếu dấu tại \({A_i}\) và \({A_{i + 1}}\)  là như nhau thì dấu tại \({A_i}\) được thay bởi dấu \(\left(  +  \right)\).

·      Nếu dấu tại \({A_i}\) và \({A_{i + 1}}\)  là khác nhau thì dấu tại \({A_i}\) được thay bởi dấu \(\left(  -  \right)\). Quy ước coi \({A_{1994}}\) là \({A_1}\).

Chứng minh rằng tồn tại số nguyên \(k \ge 2\) sao cho khi thực hiện liên tục k lần phép thay dấu nói trên, ta được đa giác \({A_1}{A_2}...{A_{1993}}\) mà dấu tại mỗi đỉnh \({A_i}\,\left( {i = 1,2,...,1993} \right)\)trùng với dấu tại chính đỉnh đó sau lần thay dấu thứ nhất.

Bài 46.                  

(Rusian MO 1995). Cho ba đống sỏi khác nhau. Sisyphus thực hiện di chuyển một viên sỏi từ một trong ba đống sỏi sang một trong hai đống sỏi còn lại. Mỗi lần chuyển sỏi, Sisyphus nhận được từ Zeus một số tiền bằng hiệu số giữa số sỏi của đống sỏi lấy đi và đống sỏi nhận thêm trước khi di chuyển. Nếu số chênh lệch này âm thì Sisyphus cũng phải trả cho Zeus số tiền chênh lệch đó. Sau một số bước thực hiện thì số sỏi mỗi đống sẽ trở về như ban đầu. Hỏi khi đó số tiền tối đa mà Sisyphus nhận được là bao nhiêu?

Bài 47.                  

(Bungary MO 1997) Ba đống sỏi có 51, 49 và 5 viên. Ta thực hiện một trong hai nước đi như sau. Một nước là dồn hai đống tuỳ ý thành một đống. Nước khác là chọn đống có số chẵn viên sỏi để chia thành hai đống bằng nhau. Hỏi có thể thực hiện một dãy các nước đi như thế để chia ba đống sỏi thành 105 đống mà mỗi đống chỉ có một viên sỏi hay không?

Bài 48.                  

(Tạp chí Kvant) Cho dãy số \(1,\,\,0,\,\,1,\,\,0,\,\,1,...\) Từ số hạng thứ  7 mỗi số bằng chữ số tận cùng của tổng 6 số hạng trước đó. Chứng minh rằng dãy số không chứa 6 số hạng liên tiếp \(0,\,\,\,1,\,\,0,\,\,1,\,\,0,\,\,\,1\).

Bài 49.                  

(VMO 1991) Có 1991 học sinh đứng thành vòng tròn và quay mặt vào giữa để chơi trò chơi đếm số như sau: Mỗi lần đếm 1 số theo chiều kim đồng hồ bắt đầu từ học sinh A nào đó. Các số đếm được là 1; 2; 3 và cứ lặp lại theo thứ tự như thế. Nếu học sinh nào đếm số 2 hoặc 3 phải rời vị trí. Học sinh nào còn lại cuối cùng sẽ được thưởng. Hỏi học sinh được thưởng đứng ở vị trí bao nhiêu cách học sinh A đếm số 1 đầu tiên?

Bài 50.                  

(VMO 1994) Tại đỉnh \({A_0}\) của một đa giác lồi \({A_0}{A_1}{A_2}...{A_n}\,\,(n \ge 3)\) ta đặt n viên bi. Thực hiện việc chuyển các viên bi theo cách sau: mỗi lần lấy một viên bi ở \({A_i}\)rồi đặt nó vào một đỉnh kề \({A_i}\) và đồng thời lấy một viên bi ở \({A_j}\) với \(i,j \in \left\{ {0;1;...;n} \right\}\)

(có thể \(i = j\)). Hãy tìm tất cả các giá trị của n sao cho sau một số hữu hạn lần hữu hạn việc chuyển bi nói trên một cách thích hợp thì ở mỗi đỉnh \({A_1},{A_2},...,{A_n}\) đều có một viên bi.