Trong không gian Oxyz, cho bốn đường thẳng: , , , . Số đường thẳng trong không gian cắt cả bốn đường thẳng trên là
D. Vô số.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Đường thẳng đi qua điểm và có một véctơ chỉ phương là .
Đường thẳng đi qua điểm và có một véctơ chỉ phương là .
Do và nên hai đường thẳng và song song với nhau.
Ta có .
Gọi là mặt phẳng chứa và khi đó có một véctơ pháp tuyến là .
Phương trình mặt phẳng là .
Gọi thì .
Gọi thì .
Do không cùng phương với nên đường thẳng AB cắt hai đường thẳng và .
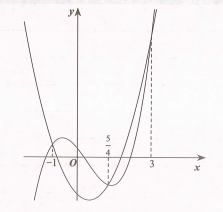
Có bao nhiêu số nguyên M thuộc khoảng để hàm số đồng biến trên ?
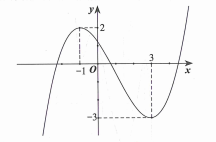
![Cho hàm số f(x) liên tục trên đoạn [-1;4] và có đồ thị trên đoạn [-1;4] như hình vẽ bên. Tích phân từ -1 đến 4 của f(x)dx bằng (ảnh 1)](https://video.vietjack.com/upload2/quiz_source1/2022/05/333-1653482408.png)
Cho hình chóp A.ABC có đáy ABCD là hình vuông cạnh a, tâm O. Cạnh bên SA=2a và vuông góc với mặt đáy (ABCD). Gọi H và K lần lượt là trung điểm của cạnh BC và CD. Tính khoảng cách giữa hai đường thẳng HK và SD.
Trên mặt phẳng Oxy ta xét một hình chữ nhật ABCD với các điểm , , , . Một con châu chấu nhảy trong hình chữ nhật đó tính cả trên cạnh hình chữ nhật sao cho chân nó luôn đáp xuống mặt phẳng tại các điểm có tọa độ nguyên (tức là điểm có cả hoành độ và tung độ đều nguyên). Tính xác suất để nó đáp xuống các điểm mà .
Gọi I là giao điểm hai tiệm cận của đồ thị hàm số . Khi đó, điểm I nằm trên đường thẳng có phương trình:
Cho hàm số f(x) có đạo hàm, liên tục trên đoạn [0;1] và thỏa mãn các điều kiện và . Tính tích phân bằng
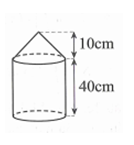
Một cái cột có hình dạng như hình bên (gồm một khối nón và một khối trụ khép lại). Chiều cao đo được ghi trên hình, chu vi đáy là 20cm. Thể tích của cột bằng