Trong các dãy số (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn? un = 2n^2 – 1...

Question

Trong các dãy số (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn? un = 2n2 - 1

VietJack · Accepted Answer

un = 2n2 – 1 + Với n ∈ N* ta có: n ≥ 1 và n2 ≥ 1 ⇒ un = 2n2 – 1 ≥ 2.12 – 1 = 1. ⇒ un ≥ 1 ⇒ dãy (un) bị chặn dưới ∀n ∈ N*. + (un) không bị chặn trên vì không có số M nào thỏa mãn: un = 2n2 – 1 ≤ M ∀n ∈N*. Vậy dãy số (un) bị chặn dưới và không bị chặn trên nên không bị chặn. Cách xét tính bị chặn của dãy số: 1) Nếu số hạng tổng quát cho dưới dạng 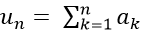thì: Thu gọn un, dựa vào biểu thức thu gọn để chặn un. Ta cũng có thể chặn tổng 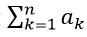bằng một tổng mà ta có thể biết được chặn trên, chặn dưới của nó. 2) Nếu dãy số (un) cho bởi một hệ thức truy hồi thì: Dự đoán chặn trên, chặn dưới rồi chứng minh bằng phương pháp chứng minh quy nạp. Ta cũng có thể xét tính đơn điệu (nếu có) sau đó giải bất phương trình un+1 − un dựa vào đó chặn (un). 3) Nếu số hạng tổng quát cho bởi công thức thì ta dựa vào phương pháp đánh giá (chú ý n ∈ N*) Bài tập liên quan: Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau: a) Dãy nghịch đảo của các số tự nhiên lẻ; b) Dãy các số tự nhiên chia cho 3 dư 1. Cách giải: a)Năm số hạng đầu: Số hạng tổng quát của dãy số: b)Năm số hạng đầu: 1;4;7;10;13 Số hạng tổng quát của dãy số: 3n + 1(n ∈ N) Tham khảo thêm một số tài liệu liên quan: Phương pháp giải và bài tập về Cách tìm số hạng tổng quát của dãy số Phương pháp giải và bài tập về Cách xét tính đơn điệu, tính bị chặn của dãy số

Câu hỏi:

Trong các dãy số (un) sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn? $u_{n} = 2 n^{2} - 1$

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Cho dãy số $(u_{n})$ , biết $u_{1} = - 1$ , $u_{n + 1} = u_{n} + 3 v ớ i n \geq 1$ .

a. Viết năm số hạng đầu của dãy số;

b. Chứng minh bằng phương pháp quy nạp: $u_{n} = 3 n - 4$

Câu 2:

Trong các dãy số $(u_{n})$ sau, dãy nào bị chặn dưới, bị chặn trên và bị chặn? $u_{n} = \sin n + \cos n .$

Câu 3:

Dãy số $(u_{n})$ cho bởi $u_{1} = 3$ , $u_{n + 1} = \sqrt{1 + {u_{n}}^{2}}, n > 1$
a. Viết năm số hạng đầu của dãy số.
b. Dự đoán công thức số hạng tổng quát un và chứng minh công thức đó bằng phương pháp quy nạp.

Câu 4:

Xét tính tăng, giảm của các dãy số $(u_{n})$ , biết: $u_{n} = \frac{2 n + 1}{5 n + 2}$

Câu 5:

Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức: $u_{n} = {(1 + \frac{1}{n})}^{n}$

Câu 6:

Xét tính tăng, giảm của các dãy số $(u_{n})$ , biết: $u_{n} = {(- 1)}^{n} . (2^{n} + 1)$

Câu 7:

Viết năm số hạng đầu của dãy số có số hạng tổng quát un cho bởi công thức: $u_{n} = \frac{2^{n} - 1}{2^{n} + 1}$

Câu 8:

Xét tính tăng, giảm của các dãy số $(u_{n})$ , biết: $u_{n} = \frac{n - 1}{n + 1}$

Câu 9:

Cho các dãy số $(u_{n})$ và $(v_{n})$ với $u_{n} = 1 + 1 / n; v_{n} = 5 n - 1$ .
a) Tính $u_{n + 1}, v_{n + 1}$ .
b) Chứng minh $u_{n + 1} < u_{n}$ và $v_{n + 1} > v_{n}$ , với mọi $n \in N^{*}$ .

Câu 10:

Viết năm số hạng đầu của dãy số có số hạng tổng quát $u_{n}$ cho bởi công thức: $u_{n} = \frac{n}{n^{2} - 1}$

Câu 11:

Xét tính tăng, giảm của các dãy số $(u_{n})$ , biết: $u_{n} = \frac{1}{n} - 2$

Câu 12:

Cho hàm số $f (n) = \frac{1}{2 n - 1}$ , n ∈ N*. Tính $f (1), f (2), f (3), f (4), f (5)$ .

Câu 13:

Viết mười số hạng đầu của dãy Phi-bô-na-xi.

Câu 14:

Viết năm số hạng đầu và số hạng tổng quát của các dãy số sau:
a) Dãy nghịch đảo của các số tự nhiên lẻ;
b) Dãy các số tự nhiên chia cho 3 dư 1.

Đề thi liên quan

Câu hỏi mới nhất