Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
A.44.000 đ.
B.41.000 đ.
C.43.000 đ.
D.42.000 đ.
Giải bởi Vietjack
Đáp án D.
Gọi \(x\) (nghìn đồng) \(\left( {30 < x < 50} \right)\) là giá bán bưởi mới để cửa hàng thu được lợi nhuận lớn nhất.
Suy ra giá bán ra đã giảm là \(50 - x\) đồng.
Số lượng bưởi bán ra đã tăng thêm là \(\frac{{50\left( {50 - x} \right)}}{5} = 500 - 10x.\)
Tổng số bưởi bán được là \(40 + 500 - 10x = 540 - 10x.\)
Doanh thu của cửa hàng là \(\left( {540 - 10x} \right)x.\)
Số tiền vốn ban đầu để mua bưởi là \(\left( {540 - 10x} \right)30.\)
Vậy lợi nhuận của cửa hàng là \(\left( {540 - 10x} \right)x - \left( {540 - 10x} \right)30 = - 10{x^2} + 840x - 16200.\)
Ta có: \(f\left( x \right) = - 10{x^2} + 840x - 16200 = - 10{\left( {x - 42} \right)^2} + 1440 \le 1440.\)
Suy ra \(\max f\left( x \right) = 1440\) khi \(x = 42.\)
Vậy giá bán mỗi quả là 42.000 đồng thì cửa hàng thu được lợi nhuận lớn nhất.
Phương pháp giải:
Bước 1: Gọi giá bán bưởi để có lợi nhuận cao nhất là \(x\) (nghìn đồng)
giá bán ra đã giảm = giá bán ban đầu – \(x\)
Bước 2:
+) Tìm số lượng quả bán được tăng thêm
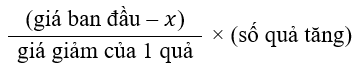
+) Tính tổng số quả bán được
= Số quả ban đầu bán được + Số quả tăng thêm
Bước 3: Tính doanh thu của cửa hàng
= Tổng số quả bán được × giá tiền lợi nhuận cao nhất
Bước 4: Tính lợi nhuận
= Doanh thu – Tổng số quả bán được × giá nhập
Ta có hàm bậc hai:
Ta quy về bài toán tìm giá trị lớn nhất, nhỏ nhất của hàm số bậc hai. Ta có thể tìm giá trị lớn nhất, nhỏ nhất dựa vào hằng đẳng thức hoặc có thể sử dụng phương pháp sau:
Xét hàm số bậc hai: . Biệt thức .
- Khi a > 0, hàm số bậc hai đạt giá trị nhỏ nhất bằng tại và hàm số có tập giá trị là .
- Khi a < 0, hàm số bậc hai đạt giá trị lớn nhất bằng tại và hàm số có tập giá trị là .
Xem thêm một số kiến thức liên quan:
Sách bài tập Toán 12 Bài 2 (Kết nối tri thức): Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Lý thuyết Giá trị lớn nhất và giá trị nhỏ nhất của hàm số (Kết nối tri thức) | Lý thuyết Toán 12
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA \bot \left( {ABCD} \right),SA = a\sqrt 3 .\) Gọi \(M\) là điểm trên đoạn \(SD\) sao cho \(MD = 2MS.\) Khoảng cách giữa hai đường thẳng \(AB\) và \(CM\) bằng
Cho hình chóp tam giác \(S.ABC,\) gọi \(M,N\) lần lượt là trung điểm của \(SB\) và \(SC.\) Tỉ số thể tích của khối chóp \(S.AMN\) và \(S.ABC\) là
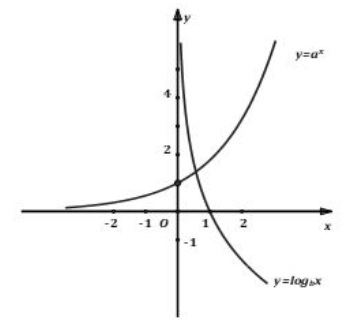
Cho đồ thị hai hàm số \(y = {a^x}\) và \(y = {\log _b}x\) như hình vẽ. Khẳng định nào sau đây đúng?
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ.
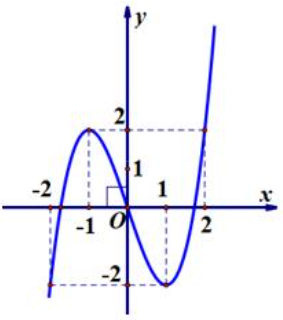
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt {4 + 2f\left( {\cos x} \right)} } \right) = m\) có nghiệm \(x \in \left[ {0;\frac{\pi }{2}} \right).\)
Có bao nhiêu giá trị nguyên dương của \(m\) để hàm số \(y = \frac{{x - 8}}{{x - m}}\) đồng biến trên từng khoảng xác định của nó?
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(3a.\) Tính thể tích \(V\) của hình chóp đã cho.
Tổng các nghiệm của phương trình \(\log _2^2\left( {3x} \right) + {\log _3}\left( {9x} \right) - 7 = 0\) bằng
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông đỉnh \(B,AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
Biết rằng phương trình \({\log _3}\left( {{x^2} - 2020x} \right) = 2021\) có 2 nghiệm \({x_1},{x_2}.\) Tính tổng \({x_1} + {x_2}.\)
Cho hàm số \(y = {x^3} - 3{x^2} + mx - 1\) với \(m\) là tham số thực. Tìm tất cả các giá trị của tham số \(m\) để hàm số đạt cực trị tại hai điểm \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 6.\)
Hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 3,BC = 4,SC = 5.\) Tam giác \(SAC\) nhọn và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right).\) Các mặt \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) tạo với nhau một góc \(\alpha \) và \(\cos \alpha = \frac{3}{{\sqrt {29} }}.\) Tính thể tích khối chóp \(S.ABCD\)
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
