Số mặt phẳng đối xứng của hình lập phương là:
A. 6.
B. 9.
C. 7.
D. 8.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B.
Có 9 mặt đối xứng của khối lập phương.
Trong đó có 3 mặt phẳng đi qua trung điểm 4 cạnh song song với nhau chia khối lập phương thành 2 khối hộp chữ nhật.
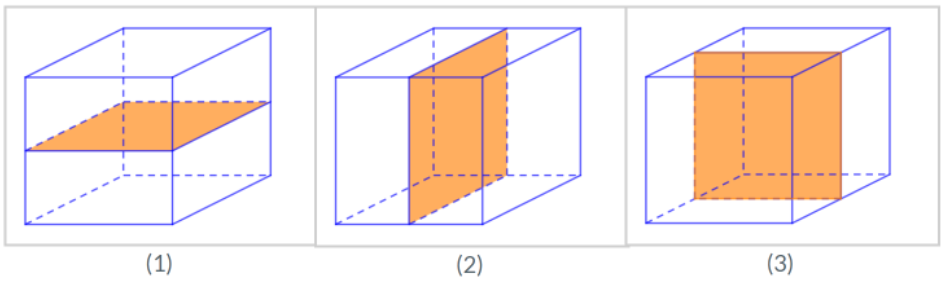
Sáu mặt còn lại chia khối lập phương thành 2 khối lăng trụ tam giác bằng nhau.
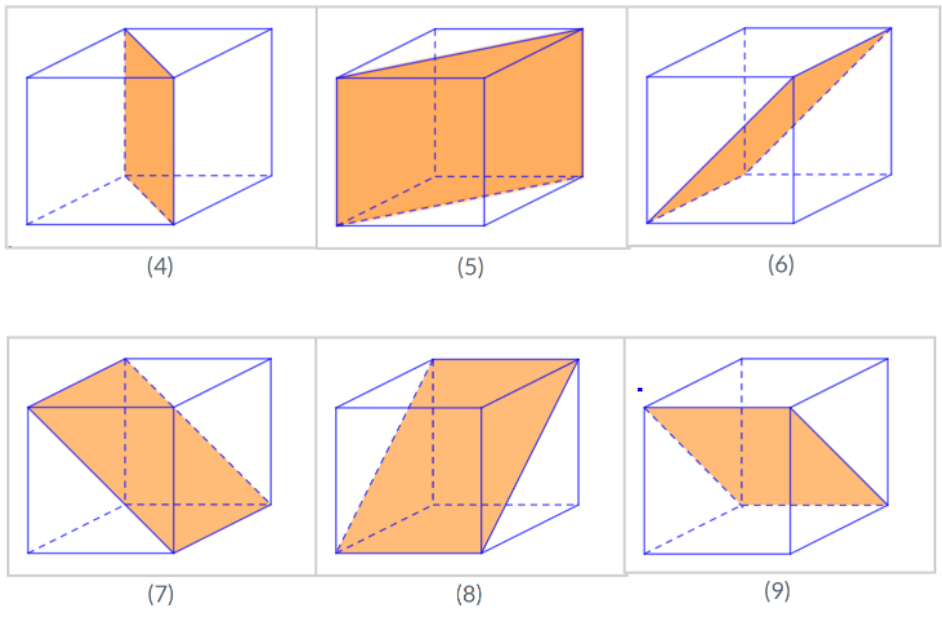
Phương pháp giải
1. Mặt Phẳng Chia Thành Khối Hộp Chữ Nhật
Có 3 mặt phẳng chia khối lập phương thành hai khối hộp chữ nhật:
Mặt phẳng qua trung điểm của cạnh đối diện và song song với cạnh còn lại
Ví dụ: Mặt phẳng ABDC, AEHG, FCEG
Các mặt phẳng này được xác định bằng việc đi qua trung điểm của các cạnh song song và đối diện, chia hình lập phương thành hai phần đối xứng qua trục chính của nó.
2. Mặt Phẳng Chia Thành Khối Lăng Trụ Tam Giác
Có 6 mặt phẳng chia khối lập phương thành hai khối lăng trụ tam giác:
Mặt phẳng đi qua trung điểm của các cạnh đối diện và phân chia khối lập phương thành hai phần đều nhau
Ví dụ: Mặt phẳng ABFE, DCGH, ADHE, BCGF
Những mặt phẳng này cắt qua các đỉnh và đường chéo của hình lập phương, phân chia mỗi nửa thành hình lăng trụ tam giác.
Xem thêm một số kiến thức liên quan:
107 câu Trắc nghiệm phép dời hình và phép đồng dạng trong các đề thi thử Toán
Chuyên đề Phép dời hình và phép đồng dạng trong mặt phẳng hay, chọn lọc
Một cửa hàng bán bưởi Đoan Hùng của Phú Thọ với giá bán mỗi quả là 50.000 đồng. Với giá này thì cửa hàng chỉ bán được khoảng 40 quả bưởi. Cửa hàng này dự định giảm giá bán, ước tính nếu cửa hàng cứ giảm mỗi quả 5000 đồng thì số bưởi bán được tăng thêm 50 quả. Xác định giá bán để cửa hàng đó thu được lợi nhuận lớn nhất, biết rằng giá nhập về ban đầu mỗi quả là 30.000 đồng.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,SA \bot \left( {ABCD} \right),SA = a\sqrt 3 .\) Gọi \(M\) là điểm trên đoạn \(SD\) sao cho \(MD = 2MS.\) Khoảng cách giữa hai đường thẳng \(AB\) và \(CM\) bằng
Cho hình chóp tam giác \(S.ABC,\) gọi \(M,N\) lần lượt là trung điểm của \(SB\) và \(SC.\) Tỉ số thể tích của khối chóp \(S.AMN\) và \(S.ABC\) là
Cho đồ thị hai hàm số \(y = {a^x}\) và \(y = {\log _b}x\) như hình vẽ. Khẳng định nào sau đây đúng?
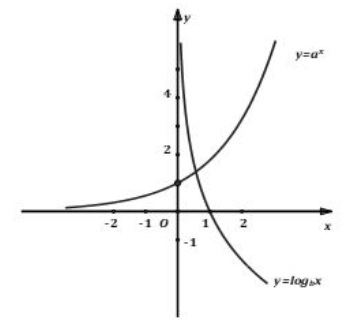
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) có đồ thị như hình vẽ.
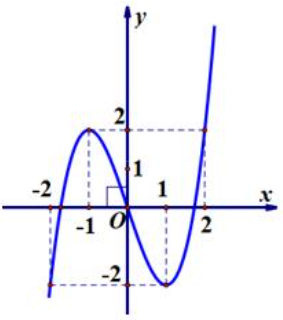
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {\sqrt {4 + 2f\left( {\cos x} \right)} } \right) = m\) có nghiệm \(x \in \left[ {0;\frac{\pi }{2}} \right).\)
Có bao nhiêu giá trị nguyên dương của \(m\) để hàm số \(y = \frac{{x - 8}}{{x - m}}\) đồng biến trên từng khoảng xác định của nó?
Cho hình chóp tứ giác đều \(S.ABCD\) có cạnh đáy bằng \(2a,\) cạnh bên bằng \(3a.\) Tính thể tích \(V\) của hình chóp đã cho.
Tổng các nghiệm của phương trình \(\log _2^2\left( {3x} \right) + {\log _3}\left( {9x} \right) - 7 = 0\) bằng
Cho hình chóp \(S.ABC\) có đáy là tam giác vuông đỉnh \(B,AB = a,SA\) vuông góc với mặt phẳng đáy và \(SA = a.\) Khoảng cách từ điểm \(A\) đến mặt phẳng \(\left( {SBC} \right)\) bằng
Biết rằng phương trình \({\log _3}\left( {{x^2} - 2020x} \right) = 2021\) có 2 nghiệm \({x_1},{x_2}.\) Tính tổng \({x_1} + {x_2}.\)
Cho hàm số \(y = {x^3} - 3{x^2} + mx - 1\) với \(m\) là tham số thực. Tìm tất cả các giá trị của tham số \(m\) để hàm số đạt cực trị tại hai điểm \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 6.\)
Hình chóp \(S.ABCD\) có đáy là hình chữ nhật với \(AB = 3,BC = 4,SC = 5.\) Tam giác \(SAC\) nhọn và nằm trong mặt phẳng vuông góc với \(\left( {ABCD} \right).\) Các mặt \(\left( {SAB} \right)\) và \(\left( {SAC} \right)\) tạo với nhau một góc \(\alpha \) và \(\cos \alpha = \frac{3}{{\sqrt {29} }}.\) Tính thể tích khối chóp \(S.ABCD\)