Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y=x^3+mx-1 / 5x^5 đồng biến...

Question

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số y=x3+mx-15x5 đồng biến với x> 0?

VietJack · Accepted Answer

+ Hàm số xác định và liên tục vớ Hiển thị đáp án Đáp án: A Giải thích: mọi x> 0. Ta có y'=3x2+m+1x6, ∀x∈0; +∞ + Hàm số đồng biến trên khoảng (0; +∞) khi và chỉ khi y'=3x2+m+1x6≥0 với mọi x> 0. ⇔m≥-3x2-1x6=g(x), ∀x∈(0;+∞)⇔m≥maxx∈(0;+∞)g(x), x∈(0;+∞).g'(x)=-6x+6x7=-6x8+6x7=0⇔x=1 Bảng biến thiên Suy ra maxg( x) = g(1) = -4 và do đó để hàm số đã cho đồng biến t với x > 0 thì m ≥ -4 Mà m nguyên âm nên m∈-4;-3;-2;-1. Chọn A. Các bước xét tính đơn điệu của hàm số y = f(x) Bước 1. Tìm tập xác định của hàm số y = f(x). Bước 2. Tính đạo hàm f'(x). Tìm các điểm xi (i = 1, 2, …, n) mà tại đó đạo hàm bằng 0 hoặc không tồn tại. Bước 3. Sắp xếp các điểm xi theo thứ tự tăng dần và lập bảng biến thiên của hàm số. Bước 4. Nêu kết luận về khoảng đồng biến, nghịch biến của hàm số. Xem thêm một số kiến thức liên quan: Lý thuyết Tính đơn điệu và cực trị của hàm số (Kết nối tri thức 2024) | Lý thuyết Toán 12 Cách xét tính đơn điệu của hàm số lượng giác

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $y = x^{3} + m x - \frac{1}{5 x^{5}}$ đồng biến với x> 0?

A. 4

B. 5

C. 3

D. 2

Trả lời:

Cách xét tính đơn điệu của hàm số lượng giác

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

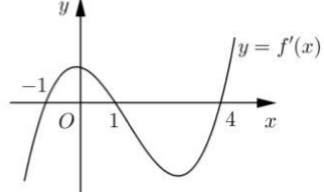
Cho hàm số y = f(x).Hàm số y= f’(x) có đồ thị như hình bên. Hỏi hàm số y= f(2-x) đồng biến trên khoảng:

Câu 2:

Tìm tất cả các giá trị thực của tham số m để đường thẳng y= - mx lần lượt cắt đồ thị của hàm số y= x³- 3x²-m+ 2 tại ba điểm phân biệt theo thứ tự A; B; C sao cho AB = BC.

Câu 3:

Cho hàm số $y = \frac{2 x + 1}{x + 1}$ có đồ thị C và d: y= x+ m. Giá trị của tham số m để d cắt C tại hai điểm phân biệt A; B sao cho tiếp tuyến tại A và B song song với nhau.

Câu 4:

Có bao nhiêu giá trị nguyên âm của tham số m để hàm số $y = |3 x^{4} - 4 x^{3} - 12 x^{2} + m|$ có 7 điểm cực trị?

Câu 5:

Câu 6:

Gọi S là tập hợp tất cả các giá trị của tham số thực m sao cho giá trị lớn nhất của hàm số $y = |x^{2} - 3 x + m|$ trên đoạn [ 0; 2] bằng 3. Số phần tử của S là

Câu 7:

Tìm tất cả các giá trị thực của tham số m để đồ thị của hàm số $y = x^{4} - 2 m x^{2}$ có ba điểm cực trị tạo thành một tam giác có diện tích nhỏ hơn 1.

Câu 8:

Cho hàm số y= x³- 3x²-m- 1 có đồ thị ( C) . Giá trị của tham số m để đồ thị C cắt trục hoành tại ba điểm phân biệt lập thành cấp số cộng là

Câu 9:

Hỏi phương trình 3x²- 6x+ ln( x+1)³+1=0 có bao nhiêu nghiệm phân biệt?

Câu 10:

Cho hàm số y= x⁴- (2m-1) x²+2m có đồ thị (C) . Có tất cả bao nhiêu giá trị nguyên của tham số m để đường thẳng d: y= 2 cắt đồ thị (C) tại bốn điểm phân biệt đều có hoành độ lớn hơn 3 là

Câu 11:

Cho hàm số y= x³- x²+ x + 1 có đồ thị ( C) . Tiếp tuyến tại điểm N( x; y) của (C) cắt đồ thị (C) tại điểm thứ hai là M( -1; -2) . Khi đó x+ y=?

Câu 12:

Cho đồ thị C: y= 2x³-3x²-1. Gọi d là đường thẳng qua A( 0; -1) có hệ số góc bằng k . Tất cả giá trị k để C cắt d tại ba điểm phân biệt là

Câu 13:

Câu 14:

Cho hàm số $y = \frac{2 x + 3}{x + 1}$ có đồ thị là (C) . Có bao nhiêu tiếp tuyến của đồ thị (C) tại những điểm thuộc đồ thị có khoảng cách đến đường thẳng d₁: 3x+ 4y-2=0 bằng 2.

Đề thi liên quan

Câu hỏi mới nhất