Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd, trong đó a

Question

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd¯ , trong đó 1≤a≤b≤c≤d≤9 .

VietJack · Accepted Answer

Đáp án B Không gian mẫu: n(Ω)=9.103=9000. Gọi A là biến cố: “số được chọn có dạng abcd¯ , trong đó ”1≤a≤b≤c≤d≤9. TH1: 1≤a=b<c<d≤9 Chọn ngẫu nhiên 4 số trong các số từ 1 đến 9 có C94=126 cách. Có duy nhất một cách xếp các chữ số a, b, c, d theo thứ tự tăng dần, do đó trường hợp này có 126 số thỏa mãn. TH2: 1≤a=b<c<d≤9 . Số cần tìm có dạng aacd¯ . Chọn ngẫu nhiên 3 số trong các số từ 1 đến 9 có C93=84 cách. Có duy nhất một cách xếp các chữ số a, c, d theo thứ tự tăng dần, do đó trường hợp này có 84 số thỏa mãn. Tương tự như vậy, các trường hợp 1≤a<b=c<d≤9, 1≤a<b<c=d≤9 , mỗi trường hợp cũng có 84 số thỏa mãn. TH3: 1≤a=b=c<d≤9 . Số cần tìm có dạng aaad¯ . Chọn ngẫu nhiên 2 số trong các số từ 1 đến 9 có C92=36 cách. Có duy nhất một cách xếp các chữ số a, d theo thứ tự tăng dần, do đó trường hợp này có 36 số thỏa mãn. Tương tự như vậy, các trường hợp 1≤a=b<c=d≤9, 1≤a<b=c=d≤9 , mỗi trường hợp cũng có 36 số thỏa mãn. TH4: 1≤a=b=c=d≤9 . Số cần tìm có dạng aaaa¯ . Có 9 số thỏa mãn ⇒n(A)=126+3.84+3.36+9=495 . Vậy P(A)=4959000=0,055 .

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng $\bar{a b c d}$ , trong đó $1 \leq a \leq b \leq c \leq d \leq 9$ .

A. 0,079.

B. 0,055.

C. 0,014.

D. 0,0495.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

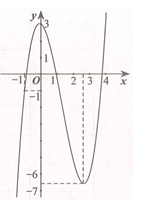
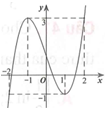
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là hình cong trong hình vẽ dưới. Đặt g(x)=f(f(x)). Tìm số nghiệm của phương trình g'(x)=0.

Câu 2:

Có bao nhiêu số hạng trong khai triển nhị thức ${(2 x - 3)}^{2018}$ thành đa thức:

Câu 3:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết $S A ⊥ (A B C D), A B = B C = a, A D = 2 a, S A = a \sqrt{2}$ . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.

Câu 4:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=|f(|x|) có tất cả bao nhiêu điểm cực trị?

Câu 5:

Câu 6:

Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số $y = - x^{3} - 3 x^{2} + m$ trên đoạn $[- 1; 1]$ bằng 0.

Câu 7:

Câu 8:

Biết $F (x)$ là nguyên hàm của hàm số $f (x) = \frac{x - \cos x}{x^{2}}$ . Hỏi đồ thị của hàm số $y = F (x)$ có bao nhiêu điểm cực trị?

Câu 9:

Cho hình chóp S.ABC có đáy là tam giác cân tại $A, A B = A C = a, \hat{B A C} = 120 °$ . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a} = - \vec{i} + 2 \vec{j} - 3 \vec{k}$ . Tìm tọa độ của vectơ $\vec{a}$ .

Câu 11:

Có thể có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng $(0; 2019)$ để $\lim \sqrt{\frac{9^{n} + 3^{n + 1}}{5^{n} + 9^{n + a}}} \leq \frac{1}{2187}$ ?

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0), B(0;0;2), C(0;-3;0) . Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

Câu 13:

Có bao nhiêu giá trị nguyên của tham số m trên đoạn $[- 2018; 2018]$ để hàm số $y = \ln (x^{2} - 2 x - m + 1)$ có tập xác định .

Câu 14:

Trong không gian Oxyz, lấy điểm C trên tia Oz sao cho OC=1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm A, B thay đổi sao cho OA+OB=OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC?

Đề thi liên quan

Câu hỏi mới nhất