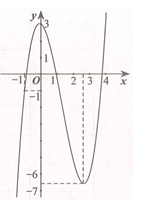
Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là hình cong trong hình vẽ dưới. Đặt g(x)=f(f(x)). Tìm số nghiệm của phương trình g'(x)=0....

Question

Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là hình cong trong hình vẽ dưới. Đặt g(x)=f(f(x)). Tìm số nghiệm của phương trình g'(x)=0.

VietJack · Accepted Answer

Đáp án C Dựa vào đồ thị hàm số y=f(x) ta thấy hàm số có hai điểm cực trị là x=0 và x=a∈(2;3) . Do đó: f'(x)=0⇔[x=0x=a∈(2;3) . Ta có: g'(x)=f'(f(x)).f'(x)=0⇔[f'(f(x))=0f'(x)=0⇔[f(x)=0 (1)f(x)=a∈(2;3) (2)f'(x)=0 (3) . Dựa vào đồ thị hàm số ta có: Phương trình (1) có 3 nghiệm phân biệt [x1∈(−1;0)x2=1x3∈(3;4). Phương trình (2) có 3 nghiệm phân biệt khác 3 nghiệm của phương trình (1). Phương trình (3) có 2 nghiệm phân biệt [x=0x=a∈(2;3). 6 nghiệm này hoàn toàn phân biệt. Vậy phương trình g'(x)=0có 6 nghiệm phân biệt. Bài tập liên quan: Cho hình trụ có thiết diện đi qua trục là một hình vuông có cạnh bằng 4a. Diện tích xung quanh của hình trụ là: A. S=4πa2. B. S=8πa2. C. S=24πa2. D. S=16πa2. Cách giải: Đáp án D Hình trụ có thiết diện đi qua trục là hình vuông có cạnh bằng 4a⇒2R=h=4a⇒R=2a với R, h lần lượt là bán kính đáy và chiều cao của hình trụ. Sxq=2πRh=2π.2a.4a=16πa2. Tham khảo thêm một số tài liệu liên quan: Đề thi tham khảo Toán 2024 Đề thi thử Toán 2024 phát triển từ đề tham khảo

Nhóm	Giá trị đại diện	Tần số	Nhóm	Giá trị đại diện	Tần số
[16,8; 19,8)	18,3	2	[16,8; 19,8)	18,3	1
[19,8; 22,8)	21,3	3	[19,8; 22,8)	21,3	2
[22,8; 25,8)	24,3	2	[22,8; 25,8)	24,3	3
[25,8; 28,8)	27,3	1	[25,8; 28,8)	27,3	2
[28,8; 31,8)	30,3	4	[28,8; 31,8)	30,3	4
		n = 12			n = 12

Câu hỏi:

Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là hình cong trong hình vẽ dưới. Đặt g(x)=f(f(x)). Tìm số nghiệm của phương trình g'(x)=0.

A. 8.

B. 4.

C. 6.

D. 2.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Có bao nhiêu số hạng trong khai triển nhị thức ${(2 x - 3)}^{2018}$ thành đa thức:

Câu 2:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết $S A ⊥ (A B C D), A B = B C = a, A D = 2 a, S A = a \sqrt{2}$ . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.

Câu 3:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=|f(|x|) có tất cả bao nhiêu điểm cực trị?

Câu 4:

Câu 5:

Câu 6:

Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số $y = - x^{3} - 3 x^{2} + m$ trên đoạn $[- 1; 1]$ bằng 0.

Câu 7:

Biết $F (x)$ là nguyên hàm của hàm số $f (x) = \frac{x - \cos x}{x^{2}}$ . Hỏi đồ thị của hàm số $y = F (x)$ có bao nhiêu điểm cực trị?

Câu 8:

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng $\bar{a b c d}$ , trong đó $1 \leq a \leq b \leq c \leq d \leq 9$ .

Câu 9:

Cho hình chóp S.ABC có đáy là tam giác cân tại $A, A B = A C = a, \hat{B A C} = 120 °$ . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a} = - \vec{i} + 2 \vec{j} - 3 \vec{k}$ . Tìm tọa độ của vectơ $\vec{a}$ .

Câu 11:

Có thể có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng $(0; 2019)$ để $\lim \sqrt{\frac{9^{n} + 3^{n + 1}}{5^{n} + 9^{n + a}}} \leq \frac{1}{2187}$ ?

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0), B(0;0;2), C(0;-3;0) . Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

Câu 13:

Có bao nhiêu giá trị nguyên của tham số m trên đoạn $[- 2018; 2018]$ để hàm số $y = \ln (x^{2} - 2 x - m + 1)$ có tập xác định .

Câu 14:

Trong không gian Oxyz, lấy điểm C trên tia Oz sao cho OC=1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm A, B thay đổi sao cho OA+OB=OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC?

Đề thi liên quan

Câu hỏi mới nhất

Câu hỏi:

Cho hàm số y=f(x) có đạo hàm trên R và có đồ thị là hình cong trong hình vẽ dưới. Đặt g(x)=f(f(x)). Tìm số nghiệm của phương trình g'(x)=0.

A. 8.

B. 4.

C. 6.

D. 2.

Trả lời:

CÂU HỎI HOT CÙNG CHỦ ĐỀ

Câu 1:

Có bao nhiêu số hạng trong khai triển nhị thức 2x−32018 thành đa thức:

Câu 2:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết SA⊥ABCD, AB=BC=a, AD=2a, SA=a2 . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.

Câu 3:

Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ. Hỏi đồ thị hàm số y=|f(|x|) có tất cả bao nhiêu điểm cực trị?

Câu 4:

Cho hình chóp S.ABC có đáy ΔABC vuông cân ở B,AC=a2,SA⊥ABC,SA=a . Gọi G là trọng tâm của ΔSBC , α đi qua AG và song song với BC chia khối chóp thành hai phần. Gọi V là thể tích của khối đa diện không chứa đỉnh S. Tính V.

Câu 5:

Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại A,AB=1cm,AC=3cm . Tam giác SAB, SAC lần lượt vuông tại B và C. Khối cầu ngoại tiếp hình chóp S.ABC có thể tích bằng 55π6cm3 . Tính khoảng cách từ C đến SAB .

Câu 6:

Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số y=−x3−3x2+m trên đoạn −1;1 bằng 0.

Câu 7:

Biết Fx là nguyên hàm của hàm số fx=x−cosxx2 . Hỏi đồ thị của hàm số y=Fx có bao nhiêu điểm cực trị?

Câu 8:

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng abcd¯ , trong đó 1≤a≤b≤c≤d≤9 .

Câu 9:

Cho hình chóp S.ABC có đáy là tam giác cân tại A,AB=AC=a, BAC^=120° . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.

Câu 10:

Trong không gian với hệ tọa độ Oxyz, cho a→=−i→+2j→−3k→ . Tìm tọa độ của vectơ a→ .

Câu 11:

Có thể có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng (0;2019) để lim9n+3n+15n+9n+a≤12187 ?

Câu 12:

Trong không gian với hệ tọa độ Oxyz, cho A(-1;0;0), B(0;0;2), C(0;-3;0) . Bán kính mặt cầu ngoại tiếp tứ diện OABC là:

Câu 13:

Có bao nhiêu giá trị nguyên của tham số m trên đoạn −2018;2018 để hàm số y=lnx2−2x−m+1 có tập xác định .

Câu 14:

Trong không gian Oxyz, lấy điểm C trên tia Oz sao cho OC=1 . Trên hai tia Ox, Oy lần lượt lấy hai điểm A, B thay đổi sao cho OA+OB=OC . Tìm giá trị nhỏ nhất của bán kính mặt cầu ngoại tiếp tứ diện O.ABC?

Đề thi liên quan

Câu hỏi mới nhất

Có bao nhiêu số hạng trong khai triển nhị thức ${(2 x - 3)}^{2018}$ thành đa thức:

Cho hình chóp S.ABCD có đáy là hình thang vuông tại A và B. Biết $S A ⊥ (A B C D), A B = B C = a, A D = 2 a, S A = a \sqrt{2}$ . Gọi E là trung điểm của AD. Tính bán kính mặt cầu đi qua các điểm A, B, C, D, E.

Tìm tất cả các giá trị của tham số m để giá trị nhỏ nhất của hàm số $y = - x^{3} - 3 x^{2} + m$ trên đoạn $[- 1; 1]$ bằng 0.

Biết $F (x)$ là nguyên hàm của hàm số $f (x) = \frac{x - \cos x}{x^{2}}$ . Hỏi đồ thị của hàm số $y = F (x)$ có bao nhiêu điểm cực trị?

Chọn ngẫu nhiên một số tự nhiên có 4 chữ số. Tính xác suất để số được chọn có dạng $\bar{a b c d}$ , trong đó $1 \leq a \leq b \leq c \leq d \leq 9$ .

Cho hình chóp S.ABC có đáy là tam giác cân tại $A, A B = A C = a, \hat{B A C} = 120 °$ . Tam giác SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Tính thể tích V của khối chóp S.ABC.

Trong không gian với hệ tọa độ Oxyz, cho $\vec{a} = - \vec{i} + 2 \vec{j} - 3 \vec{k}$ . Tìm tọa độ của vectơ $\vec{a}$ .

Có thể có tất cả bao nhiêu giá trị nguyên của tham số a thuộc khoảng $(0; 2019)$ để $\lim \sqrt{\frac{9^{n} + 3^{n + 1}}{5^{n} + 9^{n + a}}} \leq \frac{1}{2187}$ ?

Có bao nhiêu giá trị nguyên của tham số m trên đoạn $[- 2018; 2018]$ để hàm số $y = \ln (x^{2} - 2 x - m + 1)$ có tập xác định .