 Giải bởi Vietjack
Giải bởi Vietjack
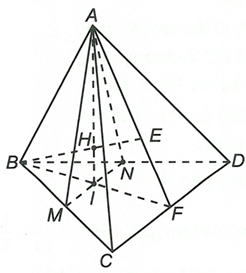
a) Vì M, N lần lượt là trung điểm của BC, BD nên MN //CD
Ta có Do MN // (ACD)
Cách chứng minh đường thẳng song song với mặt phẳng:
+ Để chứng minh một đường thẳng a song song với mặt phẳng (P) ta chứng minh a // b trong đó b ⊂ mp(P)
+ Để chứng minh hai đường thẳng song song ta dùng tính chất đường trung bình của tam giác ; đường trung bình của hình thang hay định lí Talet đảo
+ Định lí: Nếu ba mặt phẳng cắt nhau theo ba giao tuyến phân biệt thì ba giao tuyến đó đôi một song song hoặc đồng quy
Bài tập liên quan:
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi I, J lần lượt là trọng tâm các tam giác SAB và SAD. E, F lần lượt là trung điểm của AB và AD. Chọn khẳng định đúng trong các khẳng định sau.
A.
B.
C.
D.
Cách giải:
Đáp án B
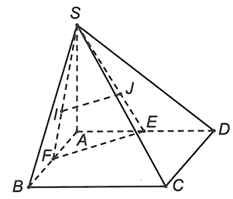
Vì I; J lần lượt là trọng tâm các tam giác SAD và SAB nên
Do nên IJ // (ABD)Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Đường thẳng và mặt phẳng song song (Kết nối tri thức) | Toán lớp 11
20 Bài tập Đường thẳng và mặt phẳng song song (sách mới) – Toán 11