 Giải bởi Vietjack
Giải bởi Vietjack

Gọi M là trung điểm của BC nên (tính chất của trọng tâm).
Xét ∆SAM, có theo định lí Ta-lét đảo suy ra GG’ // SA
Bài tập liên quan:
Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với
A. đường thẳng AD
B. đường thẳng AB
C. đường thẳng AC
D. đường thẳng BD
Cách giải:
Đáp án A
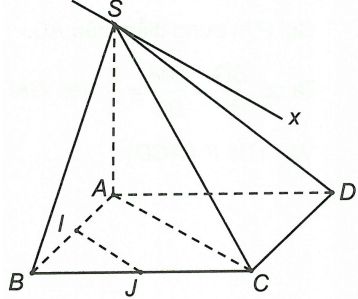
Xét hai mặt phẳng (SAC) và (SIJ) ta có S là điểm chung IJ // AC (đường trung bình trong tam giác).
Suy ta giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng qua S song song với AC
Tham khảo thêm một số tài liệu liên quan:
Chuyên đề Đại cương về đường thẳng và mặt phẳng 2023 hay, chọn lọc
Phương pháp giải về Hai đường thẳng song song 2023 (lý thuyết và bài tập)
Cho hình chóp S.ABCD có đáy là hình bình hành. Giao tuyến của mặt phẳng (SAD) và mặt phẳng (SBC) là đường thẳng song song với đường thẳng nào sau đây
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. . Gọi E, G lần lượt là trung điểm của SA và SB. M là điểm tùy ý trên cạnh BC (không trùng với B, C).
a) Xác định giao tuyến của các mặt phẳng (SAB) và (SCD); (SAD) và (SBC)
Cho hình chóp S.ABCD. Gọi I, J lần lượt là trung điểm của AB và BC. Giao tuyến của hai mặt phẳng (SAC) và (SIJ) là một đường thẳng song song với
b) Tìm giao điểm P của SC và mặt phẳng (AND). Kéo dài AN và DP cắt nhau tại I.
Chứng minh SI // AB // CD
Cho hình chóp S.ABCD đáy ABCD là hình bình hành. Gọi M, N, P, Q là các điểm lần lượt trên BC, SC, SD, AD sao cho MN // BS, NP // CD, MQ // CD
a) Chứng minh PQ // SA
Cho hình chóp S.ABCD đáy ABCD là hình thang với cạnh đáy AB và CD . Gọi M, N lần lượt là trung điểm của SA, SB.
a) Chứng minh MN // CD