Cho hình bình hành ABCD. Gọi I và K lần lượt là trung điểm của các cạnh AB và CD; E và F lần lượt là giao điểm của AK và CI với BD.
a) Chứng minh tứ giác AEFI là hình thang.
Giải bởi Vietjack
a)
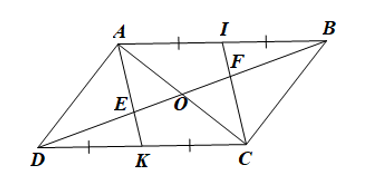
Do ABCD là hình bình hành nên AB = CD và AB // CD.
Vì I là trung điểm của AB nên .
Vì K là trung điểm của CD nên .
Do đó AI = CK.
Tứ giác AICK có AI // CK (do AB // CD) và AI = CK nên là hình bình hành (dấu hiệu nhận biết).
Suy ra AK // CI hay AE // IF.
Tứ giác AEFI có AE // IF nên là hình thang.
Lý thuyết Hình thang
• Hình thang là tứ giác có hai cạnh đối song song
Hình thang ABCD (AB // CD):
AB và CD gọi là các cạnh đáy ( hoặc đáy). AB là đáy nhỏ, CD là đáy lớn.
AD và BC gọi là các cạnh bên.
Gọi AH là đường cao kẻ từ A đến CD. Khi đó, AH là đường cao của hình thang.
• Các trường hợp đặc biệt của hình thang:
- Hình thang vuông: là hình thang có một góc vuông.
- Hình thang cân: là hình thang có hai góc kề một cạnh đáy bằng nhau.
• Tính chất về góc: Hai góc kề một cạnh bên của hình thang có tổng bằng 1800 ( nằm ở vị trí trong cùng phía của hai đoạn thẳng song song là hai cạnh đáy)
Hình thang ABCD ( AB // CD) có:
Tham khảo thêm một số tài liệu liên quan:
Lý thuyết Hình bình hành – Hình thoi (Chân trời sáng tạo) | Lý thuyết Toán lớp 8
20 câu Trắc nghiệm Hình bình hành – Hình thoi (Chân trời sáng tạo) - Toán lớp 8
Cần thêm một điều kiện gì để mỗi tứ giác trong Hình 19 trở thành hình bình hành?
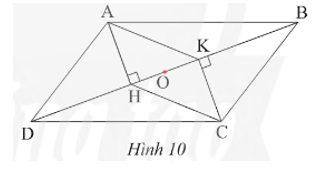
Quan sát Hình 10, cho biết ABCD và AKCH đều là hình bình hành. Chứng minh ba đoạn thẳng AC, BD và HK có cùng trung điểm O.
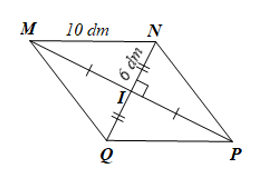
Cho hình thoi MNPQ có I là giao điểm của hai đường chéo.
a) Tính MP khi biết MN = 10 dm, IN = 6 dm.
.
b) Gọi O là giao điểm của hai đường chéo của hình bình hành ABCD. Chứng minh rằng ba điểm E, O, F thẳng hàng.
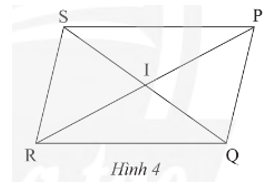
Cho hình bình hành PQRS với I là giao điểm của hai đường chéo (Hình 4). Hãy chỉ ra các đoạn thẳng bằng nhau và các góc bằng nhau có trong hình.
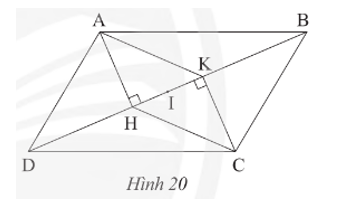
Cho hình bình hành ABCD, kẻ AH vuông góc với BD tại H và CK vuông góc với BD tại K (Hình 20).
a) Chứng minh tứ giác AHCK là hình bình hành.
Cho tam giác ABC cân tại A, gọi M là trung điểm của BC. Lấy điểm D đối xứng với điểm A qua BC.
a) Chứng minh tứ giác ABDC là hình thoi.
Cho hình thoi ABCD, hai đường chéo AC và BD cắt nhau tại O. Biết AC = 6 cm, BD = 8 cm. Tính độ dài cạnh của hình thoi ABCD.
Một tứ giác có chu vi là 52 cm và một đường chéo là 24 cm. Tìm độ dài của mỗi cạnh và đường chéo còn lại nếu biết hai đường chéo vuông góc tại trung điểm của mỗi đường.
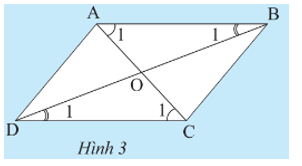
Cho tứ giác ABCD có các cạnh đối song song. Gọi O là giao điểm của hai đường chéo. Hãy chứng tỏ:
‒ Tam giác ABC bằng tam giác CDA.
‒ Tam giác OAB bằng tam giác OCD.
b) Gọi E, F lần lượt là trung điểm của AB và AC, lấy điểm O sao cho E là trung điểm của OM. Chứng minh hai tam giác AOB và MBO vuông và bằng nhau.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
