Cho hình vuông ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA (Hình 6). Đẳng thức nào sau đây đúng?
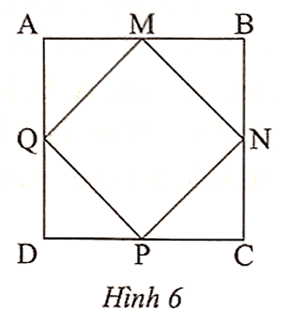
A. SMNPQ = \[\frac{1}{4}\]SABCD ;
B. SMNPQ = \[\frac{1}{3}\]SABCD ;
C. SMNPQ = SABCD ;
D. SMNPQ = \[\frac{1}{2}\]SABCD .
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: D
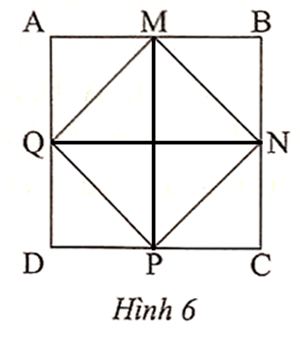
Vì ABCD là hình vuông và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên
AM = MB = BN = NC = CP = PD = DQ = QA.
Suy ra AM2 + QA2 = MB2 + BN2 = NC2 + CP2 = PD2 + DQ2,
Khi đó MQ2 = MN2 = NP2 = PQ2 hay MQ = MN = NP = PQ,
Do đó tứ giác MNPQ là hình thoi (1)
• Vì AM = AQ nên ∆AMQ vuông cân tại A, suy ra \[\widehat {AMQ}\] = 45°.
• Vì BM = BN nên ∆BMN vuông cân tại B, suy ra \[\widehat {BMN}\] = 45°.
Mà \[\widehat {AMQ}\]+ \[\widehat {QMN}\] + \[\widehat {BMN}\] = 180°, suy ra \[\widehat {QMN}\] = 90° (2)
Từ (1) và (2) suy ra MNPQ là hình vuông.
SABCD = AB2 ; SMNPQ = MQ2
MQ2 = AM2 + QA2 = \[{\left( {\frac{1}{2}AB} \right)^2}\]+ \[{\left( {\frac{1}{2}AD} \right)^2}\]
= \[\frac{1}{4}\]AB2 + \[\frac{1}{4}\]AD2 = \[\frac{1}{4}\]AB2 + \[\frac{1}{4}\]AB2 = \[\frac{1}{2}\]AB2.
Do đó SMNPQ = \[\frac{1}{2}\]SABCD.
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tia phân giác của \[\widehat {ABC}\] cắt AC tại D.
Tia phân giác của \[\widehat {ACB}\]cắt BD ở I. Gọi M là trung điểm BC. Chứng minh \[\widehat {BIM}\]= 90°.
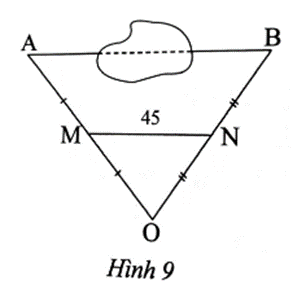
Để đo khoảng cách giữa hai điểm A và B bị ngăn cách bởi một hồ nước, người ta đóng các cọc tại các vị trí A, B, M, N, O như Hình 9 và đo được MN = 45 m. Tính khoảng cách AB biết M, N lần lượt là trung điểm OA, OB.
Cho tam giác ABC vuông tại A có AB = 6 cm, AC = 8 cm. Tia phân giác của \[\widehat {ABC}\] cắt AC tại D.
Tính độ dài DA, DC;Cho hình thang ABCD (AB // CD) và DE = EC (Hình 8). Gọi O là giao điểm của AC và BD, K là giao điểm của EO và AB. Trong các khẳng định sau đây, có bao nhiêu khẳng định đúng?
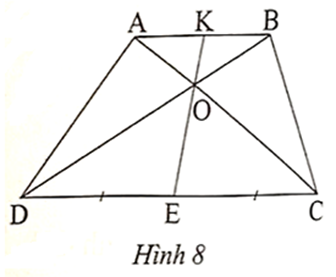
(I) \[\frac{{AK}}{{EC}} = \frac{{KB}}{{DE}}\];
(II) AK = KB ;
(III) \[\frac{{AO}}{{AC}} = \frac{{AB}}{{DC}}\];
(IV) \[\frac{{AK}}{{EC}} = \frac{{OB}}{{OD}}\].
A. 1;
B. 2;
C. 3;
D. 4.
Quan sát Hình 1. Biết MN = 1 cm, MM' // NN', OM' = 3 cm, MM' = 1,5 cm, độ dài đoạn thẳng OM trong Hình 1 là
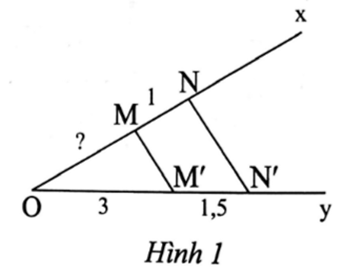
A. 3 cm;
B. 1,5 cm;
C. 2 cm;
D. 2,5 cm.
Cho tam giác ABC đều cạnh bằng 1 dm. Gọi E, F lần lượt là trung điẻm AB, AC. Chu vi hình thang EFCB bằng:
A. \[\frac{5}{2}\]dm ;
B. 3 dm ;
C. 3,5 dm ;
D. 4 dm .
Cho hình bình hành ABCD có M, N lần lượt là trung điểm BC, AD. Vẽ MP // BD (P ∈ AC) và NQ // BD (Q ∈ AC). Phát biểu nào sau đây đúng?
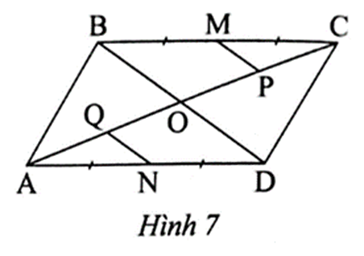
A. AQ = QP = PC ;
B. O là trung điểm PQ ;
C. MNPQ là hình bình hành ;
D. MNPQ là hình chữ nhật.
Cho tam giác ABC có cạnh BC = 10 cm. Trên cạnh AB lấy các điểm D, E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC lần lượt tại M và N. Tính độ dài DM và EN.
Cho tam giác ABC có I ∈ AB và K ∈ AC. Kẻ IM // BK (M ∈ AC), KN // CI (N ∈ AB). Chứng minh MN // BC.
Cho hai đoạn thẳng AB = 12 cm, CD = 10 cm. Tỉ số của hai đường thẳng AB và CD là
A. \[\frac{{AB}}{{CD}} = \frac{5}{6}\];
B. \[\frac{{AB}}{{CD}} = \frac{6}{5}\];
C. \[\frac{{AB}}{{CD}} = \frac{4}{3}\];
D. \[\frac{{AB}}{{CD}} = \frac{3}{4}\].
Trong Hình 2 có \[{\widehat M_1} = {\widehat M_2}\]. Đẳng thức nào sau đây đúng?
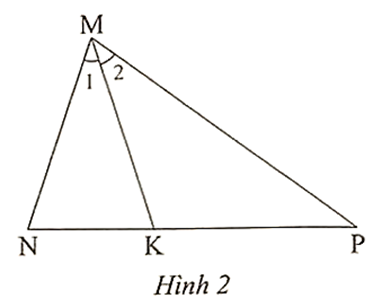
A. \[\frac{{MN}}{{MK}} = \frac{{MK}}{{KP}}\];
B. \[\frac{{MN}}{{KP}} = \frac{{MP}}{{NP}}\];
C. \[\frac{{MK}}{{MP}} = \frac{{NK}}{{KP}}\];
D. \[\frac{{MN}}{{NK}} = \frac{{MP}}{{KP}}\].
Trong Hình 5 có MQ là tia phân giác của \[\widehat {NMP}\]. Tỉ số \[\frac{x}{y}\] là
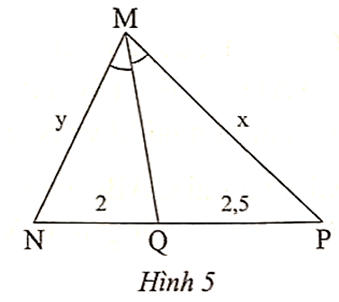
A. \[\frac{5}{2}\];
B. \[\frac{5}{4}\];
C. \[\frac{4}{5}\];
D. \[\frac{2}{5}\].