Cho các điểm A, B, C, D như hình dưới đây. Biết ∆ADC = ∆BCD, hãy chứng minh ∆ADB = ∆BCA.
 Giải bởi Vietjack
Giải bởi Vietjack
Vì ∆ADC = ∆BCD nên AD = BC và BD = AC.
Hai tam giác ADB và BCA có:
AD = BC, BD = CA (theo chứng minh trên);
AB là cạnh chung.
Vậy ∆ADB = ∆BCA (c – c – c).
Cho tam giác ABC và cho Bx, Cy lần lượt là các tia đối của các tia Ba, CA. Biết . Hãy tính số đo góc BAC.
Cho tam giác ABC có và điểm M nằm trên cạnh BC sao cho . Tính số đo các góc .
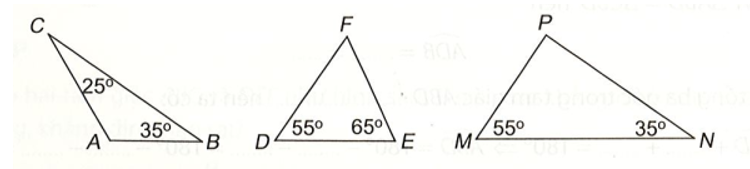
Tính số đo góc còn lại trong mỗi tam giác dưới đây. Hãy chỉ ra tam giác nào là tam giác vuông.
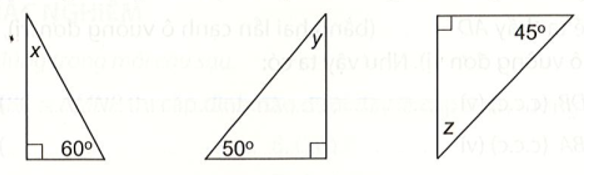
Các số đo x, y, z trong mỗi tam giác vuông dưới đây bằng bao nhiêu độ?