a) Tính tổng số đo các góc ngoài của tứ giác, ngũ giác, thập giác,

b) Chứng minh tổng số đo các góc ngoài của một đa giác (lồi) là 360°.

a) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của tứ giác (lồi) là 180⁰ Þ Tổng số đo các góc trong và các góc ngoài của tứ giacs là 4.180⁰ = 720⁰.

Mặt khác, tổng số đo các góc trong của tứ giác là: (4-2).180⁰ = 360⁰.

Þ Tổng số đo các góc ngoài của tứ giác là: 720⁰ - 360⁰ = 360⁰

Tương tự, ta cũng tính được tổng số đo các góc ngoài của ngũ giác và thập giác là 360⁰.

b) Tổng số đo của góc trong và góc ngoài ở mỗi đỉnh của hình n - giác (lồi) là 180⁰ Þ Tổng số đo các góc trong và các góc ngoài của đa giác là n.180⁰.

Mặt khác, tổng số đo các góc trong của đa giác là (n - 2).180⁰.

Þ Tổng số đo các góc ngoài của đa giác là:

n.180⁰ - (n - 2).180⁰ = 360⁰.

Lý thuyết

1. Đa giác

- Đa giác $A_1{A}_2\mathrm{...}{A}_n$ là hình gồm n đoạn thẳng $A_1{A}_2$; $A_2{A}_3$; …; $A_n{A}_1$ trong đó không có bất kỳ hai đoạn thẳng nào có một điểm chung cùng nằm trên một đường thẳng.

                                           

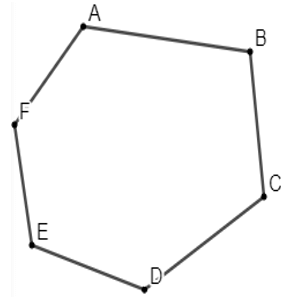
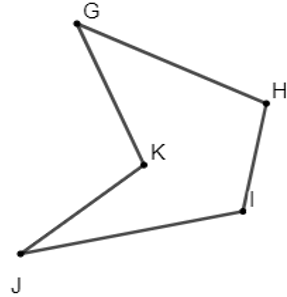
              Hình a                              Hình b

Hình a là đa giác ABCDEF là hình gồm 6 cạnh hay còn gọi là lục giác

Hình b là đa giác GHIJK là hình gồm 5 cạnh hay còn gọi là ngũ giác

- Đa giác có n đỉnh gọi là hình n – giác hay hình n cạnh.

- Đường chéo của đa giác là đoạn thẳng nối hai đỉnh không kề nhau của đa giác đó.

- Số đường chéo của đa giác được tính theo công thức:

$\frac{n\left(n-3\right)}{2}$ với n là số đỉnh của đa giác và n > 3

- Tổng số đo các góc trong một hình n – giác là:

$\left(n-2\right).180°$ với n là số đỉnh, n > 2

2. Đa giác lồi

Đa giác lồi là đa giác luôn nằm trên nửa mặt phẳng với bờ là đường thẳng chứa một cạnh bất kỳ của đa giác.

Đa giác ABCDEF là một đa giác lồi do đa giác luôn nằm trên nửa mặt phẳng có bờ là một đường thẳng chứa một cạnh bất kỳ của đa giác.

Đa giác GHIJK không phải đa giác lồi vì đa giác không nằm hoàn toàn trên nửa mặt phẳng có bờ là đường thẳng chứa cạnh JK.

Chú ý: Từ nay, khi nói đến đa giác mà không chú thích gì thêm, ta hiểu đó là đa giác lồi.

Xem thêm một số kiến thức liên quan:

50 Bài tập Đa giác. Đa giác đều (có đáp án)- Toán 8

Lý thuyết Đa giác, đa giác đều (mới 2023 + bài tập) - Toán 8