Nhằm mục đích giúp học sinh nắm vững được cấu trúc và các dạng toán hay có trong đề thi vào lớp 6 môn Toán, Tailieumoi.vn biên soạn tài liệu Cách giải toán bằng sơ đồ Ven có lời giải đầy đủ phương pháp giải, ví dụ minh họa và bài tập tự luyện giúp học sinh ôn luyện và đạt điểm cao trong kì thi tuyển sinh vào lớp 6 môn Toán.

Cách giải toán bằng sơ đồ Ven có lời giải

1. Phương pháp

Gồm 3 bước:
+ Bước 1: Chuyển bài toán về ngôn ngữ tập hợp.
+ Bước 2: Sử dụng sơ đồ Ven để minh họa các tập hợp.
+ Bước 3: Dựa vào sơ đồ Ven ta thiết lập được đẳng thức hoặc phương trình, hệ phương trình, từ đó tìm được kết quả bài toán.

2. Ví dụ

Ví dụ 1. Để phục vụ cho hội nghị quốc tế, ban tổ chức đã huy động 30 cán bộ phiên dịch tiếng Anh, 25 cán bộ phiên dịch tiếng Pháp, trong đó 12 cán bộ phiên dịch được cả 2 thứ tiếng Anh và Pháp. Hỏi:
a) Ban tổ chức đã huy động tất cả bao nhiêu cán bộ phiên dịch cho hội nghị đó.
 b) Có bao nhiêu cán bộ chỉ dịch được tiếng Anh, chỉ dịch được tiếng Pháp?

Bài giải

Số lượng cán bộ phiên dịch được ban tổ chức huy động cho hội nghị ta mô tả bằng sơ đồ Ven.

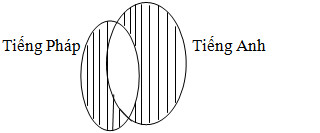
Nhìn vào sơ đồ ta có:
Số cán bộ chỉ phiên dịch được tiếng Anh là:30 – 12 = 18 (người)
Số cán bộ chỉ phiên dịch được tiếng Pháp là:25 – 12 = 13 (người)
Số cán bộ phiên dịch được ban tổ chức huy động là:30 + 13 = 43 (người)
 Đáp số: 43; 18; 13 người.

Ví dụ 2. Trong 1 hội nghị có 100 đại biểu tham dự, mỗi đại biểu nói được một hoặc hai trong ba thứ tiếng: Nga, Anh hoặc Pháp. Có 39 đại biểu chỉ nói được tiếng Anh, 35 đại biểu nói được tiếng Pháp, 8 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi có bao nhiêu đại biểu chỉ nói được tiếng Nga?

Bài giải

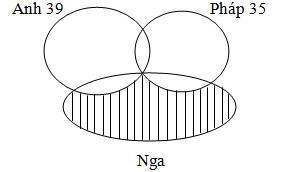
Số đại biểu nói được tiếng Pháp hoặc Nga là:

100 – 39 = 61 (đại biểu)
 Số đại biểu nói được tiếng Nga nhưng không nói được tiếng Pháp là:

61 – 35 = 26 (đại biểu)
 Số đại biểu chỉ nói được tiếng Nga là:

26 – 8 = 18 (đại biểu)
Đáp số: 18 đại biểu

Ví dụ 3. Có 200 học sinh trường chuyên ngữ tham gia dạ hội tiếng Nga, Trung và Anh. Có 60 bạn chỉ nói được tiếng Anh, 80 bạn nói được tiếng Nga, 90 bạn nói được tiếng Trung. Có 20 bạn nói được 2 thứ tiếng Nga và Trung. Hỏi có bao nhiêu bạn nói được 3 thứ tiếng?

Bài giải

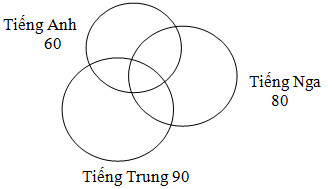
Số học sinh nói được tiếng Nga hoặc tiếng Trung là:

200 – 60 = 140 (bạn)
 Số học sinh nói được 2 thứ tiếng Nga và Trung là:

(90 + 80) – 140 = 30 (bạn)
 Số học sinh nói được cả 3 thứ tiếng là:

30 – 20 = 10 (bạn)
Đáp số: 10 bạn.

3. BÀI TẬP VẬN DỤNG

Bài 1. Lớp 4A có 30 em tham gia dạ hội tiếng Anh và tiếng Trung, trong đó có 25 em nói được tiếng Anh và 18 em nói được tiếng Trung. Hỏi có bao nhiêu bạn nói được cả 2 thứ tiếng?

Bài 2. Lớp học có 53 học sinh, qua điều tra thấy 40 em thích học môn Văn, 30 em thích học môn Toán. Hỏi có nhiều nhất bao nhiêu học sinh thích học 2 môn? Có ít nhất bao nhiêu học sinh thích học 2 môn? Nếu có 3 học sinh không thích học 2 môn thì lúc này có bao nhiêu học sinh thích học 2 môn.

Bài 3. Lớp 5A có 15 ban đăng kí học ngoại khoá môn Văn, 12 bạn đăng kí học ngoại khoá môn Toán, trong đó có 7 bạn đăng kí học cả Văn và Toán. Hỏi:
a) Có bao nhiêu bạn đăng kí học Văn hoặc Toán?
b) Có bao nhiêu bạn chỉ đăng kí học Văn? chỉ đăng kí học Toán?
Bài 4. Trên 1 hội nghị các đại biểu sử dụng một hoặc hai trong 3 thứ tiếng: Nga, Anh hoặc Pháp. Có 30 đại biểu nói được tiếng Pháp, 35 đại biểu chỉ nói được tiếng Anh, 20 đại biểu chỉ nói được tiếng Nga và 15 đại biểu nói được cả tiếng Anh và tiếng Nga. Hỏi hội nghị đó có bao nhiêu đại biểu tham dự?
Bài 5. Bốn mươi em học sinh của trường X dự thi 3 môn: ném tạ, chạy và đá cầu. Trong đội có 8 em chỉ thi ném tạ, 20 em thi chạy và 18 em thi đá cầu. Hỏi có bao nhiêu em vừa thi chạy vừa thi đá cầu?
Bài 6. Đội tuyển thi học sinh giỏi của tỉnh X có 25 em thi Văn và 27 em thi toán, trong đó có 18 em vừa thi Văn vừa thi toán. Hỏi đội tuyển học sinh giỏi 2 môn Văn và Toán của tỉnh X có bao nhiêu em?

Bài 7. Lớp 5A có 35 học sinh làm bài kiểm tra Toán. Đề bài gồm có 3 bài toán. Sau khi kiểm tra, cô giáo tổng hợp được kết quả như sau:  Có 20 em giải được bài toán thứ nhất, 14 em giải được bài toán thứ hai, 10 em giải được bài toán thứ ba, 5 em giải được bài toán thứ hai và thứ ba, 2 em giải được bài toán thứ nhất và thứ hai,6 em làm được bài toán thứ nhất và thứ ba, chỉ có 1 học sinh đạt điểm 10 vì đã giải được cả 3 bài. Hỏi lớp học đó có bao nhiêu học sinh không giải được bài toán nào?