Với tóm tắt lý thuyết Toán lớp 7 Bài 2: Phân tích và xử lí dữ liệu sách Cánh diều hay, chi tiết cùng với bài tập tự luyện chọn lọc giúp học sinh nắm vững kiến thức trọng tâm, ôn luyện để học tốt môn Toán lớp 7.

Lý thuyết Toán lớp 7 Bài 2: Phân tích và xử lí dữ liệu

A. Lý thuyết

1. Phân tích và xử lí dữ liệu để rút ra kết luận

Sau khi thu thập, tổ chức, phân loại, biểu diễn dữ liệu bằng bảng hoặc biểu đồ, ta cần phân tích và xử lí các dữ liệu đó để tìm ra những thông tin hữu ích và rút ra kết luận. Thông thường, quá trình phân tích và xử lí dữ liệu dựa trên tính toán và suy luận toán học.

Ví dụ: Một công ty gồm có bốn đội công nhân may áo khoác jeans. Năng suất may được số lượng áo khoác jeans của bốn đội công nhân đó trong 2 tháng đầu năm được biểu diễn như trong biểu đồ sau:

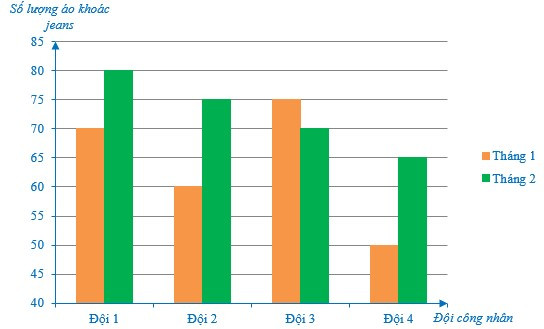
a) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn.

b) Sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn.

c) Đội công nhân nào may được nhiều nhất ở mỗi tháng?

d) Đội công nhân nào may được ít nhất ở mỗi tháng?

e) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được nhiều nhất?

f) Trong cả hai tháng, đội công nhân nào có tổng số áo sơ mi may được ít nhất?

Hướng dẫn giải

a) Ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 1 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 2; Đội 1; Đội 3.

b) Ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Vậy khi sắp xếp các đội công nhân theo số lượng áo khoác jeans may được ở tháng 2 theo thứ tự từ nhỏ đến lớn, ta được: Đội 4; Đội 3; Đội 2; Đội 1.

c) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 3 may được nhiều áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 1 may được nhiều áo khoác jeans nhất.

Vậy đội công nhân may được nhiều áo khoác jeans nhất ở tháng 1, tháng 2 lần lượt là Đội 3 và Đội 1.

d) Ở tháng 1, ta có 50 < 60 < 70 < 75 (áo khoác jeans).

Do đó ở tháng 1, Đội 4 may được ít áo khoác jeans nhất.

Ở tháng 2, ta có 65 < 70 < 75 < 80 (áo khoác jeans).

Do đó ở tháng 2, Đội 4 may được ít áo khoác jeans nhất.

Vậy đội công nhân may được ít áo khoác jeans nhất ở tháng 1, tháng 2 đều là Đội 4.

e) Tổng số áo khoác jeans Đội 1 may được ở cả hai tháng là:

70 + 80 = 150 (áo khoác jeans).

Tổng số áo khoác jeans Đội 2 may được ở cả hai tháng là:

60 + 75 = 135 (áo khoác jeans).

Tổng số áo khoác jeans Đội 3 may được ở cả hai tháng là:

75 + 70 = 145 (áo khoác jeans).

Tổng số áo khoác jeans Đội 4 may được ở cả hai tháng là:

50 + 65 = 115 (áo khoác jeans).

Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 1 có tổng số áo sơ mi may được nhiều nhất.

f) Ta có 115 < 135 < 145 < 150 (áo khoác jeans).

Vậy trong cả hai tháng, Đội 4 có tổng số áo sơ mi may được ít nhất.

2. Tính hợp lí của kết luận thống kê

Quá trình phân tích và xử lí dữ liệu giúp chúng ta có thể nhận biết được: tính hợp lí của dữ liệu thống kê, tính hợp lí của kết luận thống kê và ta cũng có thể bác bỏ kết luận đã nêu ra. Thông thường, để làm được điều đó ta dựa trên những tiêu chí đơn giản hoặc dựa trên tính toán và suy luận toán học.

Ví dụ: Một huấn luyện viên dạy bơi sải ghi lại thời gian (tính theo buổi, mỗi buổi 90 phút) thành thạo môn bơi sải của các học viên như bảng bên:

a) Huấn luyện viên đã khảo sát tổng cộng bao nhiêu học viên?

b) Biết rằng học viên có năng khiếu về môn bơi lội sẽ thành thạo bơi sải trong vòng 8 buổi học. Huấn luyện viên đã đưa ra kết luận rằng: Sau khi khảo sát, số học viên có năng khiếu về môn bơi lội chiếm tỉ lệ 15% so với tổng số học viên tham gia khảo sát. Hỏi kết luận đó của huấn luyện viên có đúng không?

Hướng dẫn giải

a) Số học viên mà huấn luyện viên đã khảo sát là:

1 + 2 + 3 + 10 + 13 + 7 + 4 = 40 (học viên).

Vậy huấn luyện viên đã khảo sát tổng cộng là 40 học viên.

b) Số học viên được huấn luyện viên đánh giá là có năng khiếu về môn bơi lội là:

1 + 2 + 3 = 6 (học viên).

So với tổng số học viên tham gia khảo sát, tỉ lệ học viên được đánh giá là có năng khiếu về môn bơi lội là:

$\frac{6.100}{40}\%=15\%$.

Vậy huấn luyện viên đã kết luận đúng.

B. Bài tập tự luyện

B.1 Bài tập tự luận

Bài 1. Biểu đồ sau đây thể hiện tỉ suất gia tăng dân số tự nhiên trung bình năm của các nhóm nước:

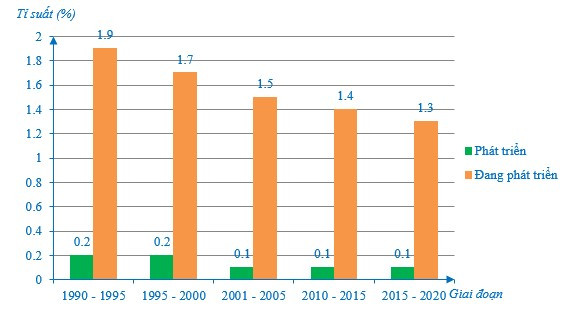
a) Lập bảng số liệu thống kê thể hiện tỉ suất gia tăng dân số tự nhiên trung bình năm của các nhóm nước.

b) Bạn Thảo kết luận rằng: Tỉ suất gia tăng dân số tự nhiên trung bình năm của nhóm nước phát triển trong giai đoạn 1990 – 2020 luôn luôn thấp hơn của nhóm nước đang phát triển. Em hãy cho biết kết luận đó đúng hay sai? Vì sao?

Hướng dẫn giải

a) Ta có bảng số liệu thống kê sau:

b) Ta xét trong mỗi giai đoạn:

+ Giai đoạn 1990 – 1995:

Ta thấy 0,2 (%) < 1,9 (%).

Do đó tỉ suất gia tăng dân số trong giai đoạn 1990 – 1995 của nhóm nước phát triển thấp hơn của nhóm nước đang phát triển.

+ Giai đoạn 1995 – 2000:

Ta thấy 0,2 (%) < 1,7 (%).

Do đó tỉ suất gia tăng dân số trong giai đoạn 1995 – 2000 của nhóm nước phát triển thấp hơn của nhóm nước đang phát triển.

+ Giai đoạn 2001 – 2005:

Ta thấy 0,1 (%) < 1,5 (%).

Do đó tỉ suất gia tăng dân số trong giai đoạn 2001 – 2005 của nhóm nước phát triển thấp hơn của nhóm nước đang phát triển.

+ Giai đoạn 2010 – 2015:

Ta thấy 0,1 (%) < 1,4 (%).

Do đó tỉ suất gia tăng dân số trong giai đoạn 2010 – 2015 của nhóm nước phát triển thấp hơn của nhóm nước đang phát triển.

+ Giai đoạn 2015 – 2020:

Ta thấy 0,1 (%) < 1,3 (%).

Do đó tỉ suất gia tăng dân số trong giai đoạn 2015 – 2020 của nhóm nước phát triển thấp hơn của nhóm nước đang phát triển.

Vậy kết luận của bạn Thảo là đúng.

Bài 2. Biểu đồ sau đây cho biết tổng kim ngạch xuất khẩu nông sản 2 tháng đầu năm của Việt Nam giai đoạn 2019 – 2020:

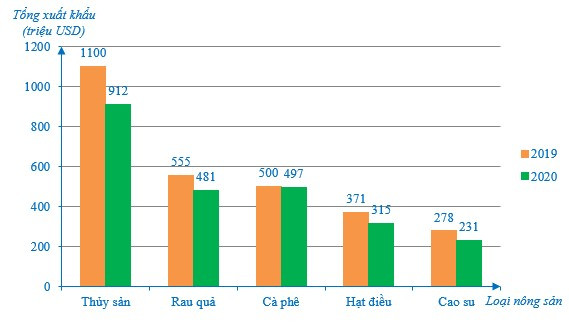
(Theo thống kê của Tổng cục Hải quan)

a) Lập bảng thống kê tổng xuất khẩu nông sản 2 tháng đầu năm giai đoạn 2019 – 2020 theo mẫu sau:

b) Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2019 cao nhất? Loại nông sản nào Việt Nam có tổng xuất khẩu năm 2020 thấp nhất?

c) Bạn An kết luận rằng: Tổng xuất khẩu thủy sản của nước ta năm 2020 giảm 18,2% so với năm 2019. Theo em, kết luận của bạn An là đúng hay sai? Vì sao?

Hướng dẫn giải

a) Dựa vào biểu đồ ta có bảng sau:

b) Nhìn vào biểu đồ cột, ta thấy:

+ Ở năm 2019, thủy sản là loại nông sản có cột biểu diễn tổng xuất khẩu cao nhất.

+ Ở năm 2020, cao su là loại nông sản có cột biểu diễn tổng xuất khẩu thấp nhất.

Vậy năm 2019 Việt Nam có tổng xuất khẩu của thủy sản cao nhất; cao su có tổng xuất khẩu năm 2020 thấp nhất.

c) Tỉ số phần trăm giữa tổng xuất khẩu thủy sản năm 2020 và tổng xuất khẩu thủy sản năm 2019 là:

$\frac{912.100}{1100}\%\approx 82,9\%$.

Do đó tổng xuất khẩu thủy sản năm 2020 giảm 100% – 82,9% = 17,1% so với năm 2019.

Ta có 17,1% ≠ 18,2%.

Vậy bạn An đã kết luận sai.

B.2 Bài tập trắc nghiệm

Câu 1. Cho biểu đồ biểu diễn kết quả học tập của học sinh khối 7.

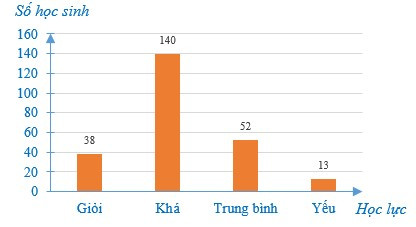
Số học sinh học lực Trung bình ít hơn số học sinh học lực Khá bao nhiêu?

A. 88 học sinh;

B. 90 học sinh;

C. 92 học sinh;

D. 94 học sinh.

Hướng dẫn giải

Đáp án đúng là: A

Số học sinh Khá là 140 và số học sinh Trung bình là 52.

Số học sinh học lực Trung bình ít hơn số lượng học sinh học lực Khá là:

140 – 52 = 88 (học sinh)

Vậy số học sinh học lực Trung bình ít hơn số học sinh học lực Khá là 88 học sinh.

Câu 2. Cho bảng thống kê số lượt khách du lịch (ước đạt) đến Ninh Bình trong các năm 2016, 2017, 2018.

Số lượt khách du lịch đến Ninh Bình trong năm 2018 tăng bao nhiêu phần trăm so với năm 2016 (làm tròn kết quả đến hàng phần trăm)?

A. 13,33%;

B. 13,34%;

C. 13,35%;

D. 13,36%.

Hướng dẫn giải

Đáp án đúng là: C

Tỉ số phần trăm số khách du lịch đến Ninh Bình trong năm 2018 so với năm 2016 là:

(7,3 : 6,44). 100% = 113,354037… % ≈ 113,35%

Vậy số lượt khách du lịch đến Ninh Bình trong năm 2018 tăng khoảng 13,35% so với năm 2016.

Câu 3. Dưới đây là biểu đồ biểu chiều cao trung bình của nam và nữ ở một số quốc gia châu Á:

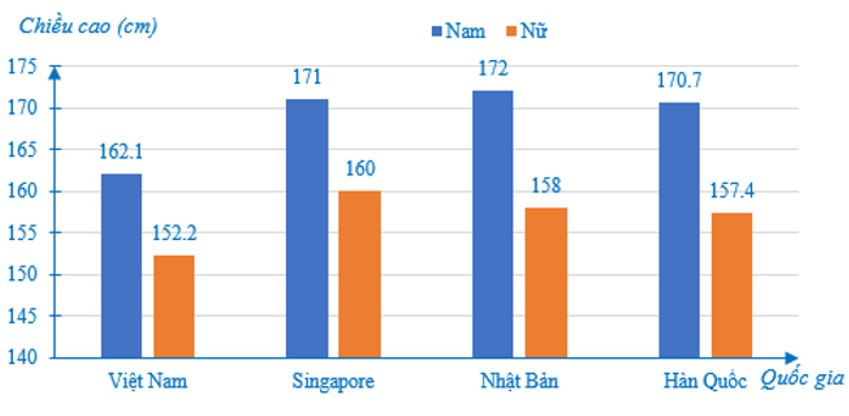
Sự chênh lệch chiều cao giữa nam và nữ ở nước nào lớn nhất?

A. Việt Nam;

B. Singapore;

C. Nhật Bản;

D. Hàn Quốc.

Hướng dẫn giải

Đáp án đúng là: C

Chênh lệch chiều cao giữa nam và nữ ở:

Việt Nam là 162,1 – 152,2 = 9,9 (cm);

Singapore là 171 – 160 = 11 (cm);

Nhật Bản là 172 – 158 = 14 (cm);

Hàn Quốc là 170,7 – 157,4 = 13,3 (cm).

Vậy sự chênh lệch chiều cao giữa nam và nữ ở Nhật Bản là lớn nhất.

Xem thêm các bài tóm tắt lý thuyết Toán lớp 7 Cánh diều hay, chi tiết khác:

Lý thuyết Bài 1: Thu nhập, phân loại và biểu diễn dữ liệu

Lý thuyết Bài 2: Phân tích và xử lí dữ liệu

Lý thuyết Bài 3: Biểu đồ đoạn thẳng

Lý thuyết Bài 4: Biểu đồ hình quạt tròn

Lý thuyết Bài 5: Biến cố trong một số trò chơi đơn giản