Tailieumoi.vn xin giới thiệu Bài tập về tỉ số phần trăm lớp 5 được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 50 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 5. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Tỉ số phần trăm. Mời các bạn đón xem:

Bài tập về tỉ số phần trăm lớp 5

A. Bài tập về tỉ số phần trăm

Dạng 1: Tìm tỉ số phần trăm của hai số

1. Phương pháp giải

Muốn tìm tỉ số phần trăm của hai số, ta làm như sau

- Tìm thương của hai số đó

- Nhân thương đó với 100 và viết thêm kí hiệu % vào bên phải tích tìm được.

2. Bài tập minh họa

Bài 1: Một lớp có 40 học sinh, trong đó có 25 học sinh nữ. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm số học sinh của cả lớp.

Hướng dẫn giải

Số học sinh nữ chiếm số phần trăm học sinh cả lớp là:

25 : 40 x 100 = 62,5 (%)

Đáp số: 62,5%

Bài 2: Theo kế hoạch, năm nay thôn Trung Dương phải trồng 20ha ngô. Nhưng đến hết năm thôn trồng được 23ha ngô. Hỏi đến hết năm thôn Trung Dương thực hiện vượt mức kế hoạch cả năm là bao nhiêu phần trăm?

Hướng dẫn giải

Thôn Trung Dương thực hiện được số phần trăm kế hoạch là:

23 : 20 x 100 = 115%

Vượt mức kế hoạch cả năm số phần trăm là:

115 – 100 = 15%

Đáp số: 15%

Dạng 2: Tìm giá trị phần trăm của một số

1. Phương pháp giải

- Muốn tìm giá trị phần trăm của một số đã cho ta lấy số đó nhân với số phần trăm rồi chia cho 100.

2. Bài tập minh họa

Bài 1: Một xưởng may đã dùng hết 545m vải để may quần áo. Trong đó số vải may quần chiếm 40% số vải may áo. Hỏi số vải may áo là bao nhiêu mét?

Số vải may quần là:

545 x 40 : 100 = 218 (m)

Số vải để may áo là:

545 – 218 = 327 (m)

Đáp số: 327m

Bài 2: Một mảnh đất hình chữ nhật có chiều dài 18m, chiều rộng 12m. Người ta dành ra 45% diện tích để xây nhà. Tính phần diện tích đất để xây nhà.

Diện tích mảnh đất là:

18 x 12 = 216 (m² )

Diện tích đất để xây nhà là:

216 x 45 : 100 = 97,2 (m² )

Đáp số: 97,2 m²

Dạng 3: Tìm một số khi biết giá trị phần trăm của số đó

1. Phương pháp giải

Muốn tìm một số khi biết giá trị phần trăm của số đó ta lấy số đó nhân 100 rồi chia cho số phần trăm.

2. Bài tập minh họa

Bài 1: Số học sinh khá giỏi của trường tiểu học Thọ An là 339 em, chiếm 30% số học toàn trường. Hỏi trường Thọ An có bao nhiêu học sinh?

Hướng dẫn giải

Số học sinh của trường Thọ An là:

339 x 100 : 30 = 1130 (học sinh)

Đáp số: 1130 học sinh

Bài 2: Một kho chưa gạo tẻ và gạo nếp, trong đó có 5,6 tấn gạo tẻ. Tính tổng số gạo trong kho biết số gạo tẻ chiếm 70% số gạo trong kho.

Hướng dẫn giải

Tổng số gạo trong kho có là:

5,6 x 100 : 70 = 8 (tấn)

Đáp số: 8 tấn

Dạng 4: Bài toán về tính lãi

1. Phương pháp

- Đọc đề bài và xác định tiền vốn (giá mua), giá bán, tiền lãi, tiền lỗ.

- Áp dụng công thức:

Giá bán = Giá mua + Lãi

Giá bán = Giá mua – Lỗ

2. Ví dụ

Ví dụ 1: Một cửa hàng định giá mua hàng bằng 75% giá bán. Hỏi cửa hàng đó định giá bán bằng bao nhiêu phần trăm giá mua?

Bài giải

Xem giá bán là 100% thì giá mua là 75%.

Vậy giá bán ra so với giá mua vào chiếm số phần trăm là:

100 : 75 = 133,33%

Đáp số: 133,33% giá mua

Ví dụ 2: Một chiếc xe đạp giá 1 700 000 đồng, nay hạ giá 15%. Hỏi giá chiếc xe đạp bây giờ là bao nhiêu?

Bài giải

Xem giá chiếc xe đạp lúc đầu là 100%, sau khi giảm chỉ còn:

100% – 15% = 85%

Giá chiếc xe đạp hiện nay là:

1 700 000 × 85 : 100 = 1 445 000(đồng)

Đáp số: 1 445 000 đồng.

Ví dụ 3: Một cửa hàng sách, hạ giá 20% giá sách nhân ngày 20/11. Tuy vậy, cửa hàng vẫn còn lãi 8%. Hỏi, ngày thường (không hạ giá) thì cửa hàng được lãi bao nhiêu phần trăm?

Bài giải

Coi giá bán ngày thường là 100% thì giá bán ngày 20/11 là:

100% - 20% = 80%

Cửa hàng vẫn còn lãi 8% tức là cửa hàng bán được:

100% + 8% = 108% (giá mua)

Số tiền lãi tính theo giá mua là:

100 : 80 × 108 = 135% (giá mua)

Vậy ngày thường thì cửa hàng lãi được:

135% - 100% = 35%

Đáp số: 35%

Dạng 5. Bài toán đưa về dạng toán quen thuộc

1. Phương pháp

Đưa về các dạng toán quen thuộc như tổng – tỉ, hiệu – tỉ, …

2. Ví dụ

Ví dụ 1. Tổng của hai số bằng 25% thương của hai số đó cũng bằng 25%. Tìm hai số đó.

Bài giải

Đổi: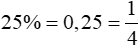  

Ta có sơ đồ:

 

Số thứ nhất là: 0,25 : (1+4) = 0,05

Số thứ hai là: 0,25 – 0,05 = 0,2

Đáp số: 0,05 và 0,2

Ví dụ 2: Tìm hai số, biết 25% số thứ nhất bằng 1/3 số thứ hai và hiệu của hai số là  15/37.

Bài giải

Đổi: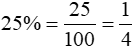  

Theo bài ra, 1/4 số thứ nhất bằng 1/3 số thứ hai. Ta có sơ đồ:

 

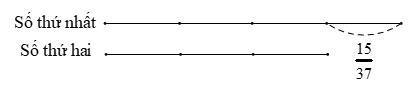
Số thứ nhất là:

 

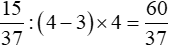
Số thứ hai là:

 

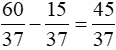
Đáp số: 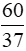  và 

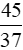
B. Bài tập về tỉ số phần trăm

1. Bài tập tự luận

Bài 1: Một người mua 4 quyển sách cùng loại, vì được giảm 15% giá bìa nên chỉ phải trả 30600 đồng. Hỏi giá bìa mỗi quyển sách là bao nhiêu?

Phương pháp giải

- Tìm giá tiền mỗi cuốn sách phải trả

- Số tiền mỗi cuốn sách phải trả so với giá bìa ứng với 85%

- Tìm giá bìa của mỗi cuốn sách

Lời giải:

Giá tiền phải trả của mỗi quyển sách là

30600 : 4 = 7650 (đồng)

Số tiền phải trả so với giá bìa thì bằng:

100% - 15 % = 85%

Giá bìa của mỗi sách là:

7650 : 85 x 100 = 9000 (đồng)

Đáp số: 9000 đồng

Bài 2: Trong tháng vừa rồi, nhà máy sản xuất được 450 sản phẩm. tính ra nhà máy đã sản xuất vượt mức 12,5% kế hoạch. Hỏi theo kế hoạch thì nhà máy phải sản xuất bao nhiêu sản phẩm?

Phương pháp giải

- Tìm số phần trăm kế hoạch nhà máy sản xuất được = 100% + 12,5% = 112,5%

- Tìm số sản phẩm cần sản xuất theo kế hoạch = số sản phẩm sản xuất được : 112,5 x 100

Lời giải:

So với kế hoạch nhà máy đã sản xuất được:

100% + 12,5% = 112,5% (kế hoạch)

Theo kế hoạch, nhà máy phải sản xuất số sản phẩm là

450 : 112,5 x 100 = 400 (sản phẩm)

Đáp số: 400 sản phẩm

Bài 3: Một người bán một cái bàn được lại 20% giá bán. Hỏi người đó được lãi bao nhiêu phần trăm giá vốn của cái bàn?

Phương pháp giải

- Coi giá bán là 100%

- Tìm số phần trăm giá vốn so với giá bán

- Tìm số phần trăm tiền lãi so với giá vốn

Lời giải:

Coi giá bán là 100%

Vì được lãi 20% giá bán nên giá vốn so với giá bán chỉ bằng

100% - 20% = 80%

So với giá vốn thì bán cái bàn lãi:

20 : 80 = 0,25 = 25%

Đáp số: 25%

Bài 4: Trong một kho chứa 20 tấn gạo tẻ và gạo nếp, số gạo nếp chiếm 5% tổng số gạo của kho. Hỏi phải đưa vào kho thêm bao nhiêu tấn gạo tẻ để trong kho có số gạo nếp bằng 2% tổng số gạo của kho?

Phương pháp giải

- Tìm số gạo nếp có trong kho

- Tìm tổng số tấn gạo trong kho để gạo nếp bằng 2% tổng số gạo 

- Tìm số gạo tẻ cần đưa thêm vào kho

Lời giải:

Số gạo nếp có trong kho là

20 x 5 : 100 = 1 (tấn)

Muốn gạo nếp bằng 2% tổng số gạo của kho thì trong kho phải có số tấn gạo là:

1 : 2 x 100 = 50 (tấn)

Số gạo tẻ phải đưa thêm vào kho là:

50 – 20  = 30 (tấn)

Đáp số: 30 tấn

Bài 5: Giá vàng tháng 2 tăng 10% so với tháng 1, sang tháng 3 lại giảm 10% so với tháng 2. Hỏi giá vàng tháng 1 và tháng 3, giá nào cao hơn?

Lời giải:

Giá vàng tháng 2 so với tháng 1 thì có số phần trăm là

100% + 10% = 110% (so với tháng 1)

Giá vàng tháng 3 so với tháng 2 thì bằng:

100% - 10% = 90% (so với tháng 2)

Giá vàng tháng 3 so với tháng 1 thì bằng:

90% x 110% = $\frac{90}{100}\times \frac{110}{100}=\frac{99}{100}=99\mathrm{\%}$ (so với tháng 1)

Vậy giá vàng tháng 1 cao hơn giá vàng tháng 3.

Bài 6: Một miếng đất hình chữ nhật có diện tích 50m², người ta tăng chiều dài miếng đất thêm 10% và giảm chiều rộng 10%. Hỏi diện tích miếng đất tăng hay giảm bao nhiêu mét vuông?

Lời giải:

Chiều dài mới so với chiều dài cũ thì bằng:

100% + 10% = 110%

Chiều rộng mới so với chiều rộng cũ thì bằng:

100% - 10% = 90%

Diện tích mới so với diện tích cũ thì bằng:

90% x 110% = $\frac{90}{100}\times \frac{110}{100}=\frac{99}{100}=99\mathrm{\%}$

Diện tích mới so với diện tích cũ thì giảm đi số phần trăm là:

100% - 99 % = 1%

Số mét vuông giảm đi là

50 x 1 : 100 = 0,5 (m²)

Đáp số: 0,5 m²

Bài 7: Một cửa hàng mua một máy sấy tóc với giá 60000 đồng. Hỏi cửa hàng phải bán lại máy sấy tóc đó với giá bao nhiêu tiền để được lãi 20% giá bán?

Phương pháp giải

- Coi giá bán là 100%

- Số phần trăm của giá mua so với giá bán = 100% - 20% = 80 %

- Giá bán của máy sấy tóc = giá mua : 80 x 100 

Lời giải:

Coi giá bán là 100%

Để được lãi 20% giá bán thì giá mua so với giá bán bằng:

100% - 20% = 80%

Giá bán của máy sấy tóc là:

60000 : 80 x 100 = 75000 (đồng)

Đáp số: 75 000 đồng

2. Bài tập vận dụng

Bài 1: Một tổ sản xuất làm được 1500 sản phẩm. Trong đó anh Hai làm được 130 sản phẩm. Hỏi anh Hai làm được bao nhiêu phần trăm số sản phẩm của tổ?

Bài 2: Một cửa hàng bỏ ra 7 500 000 triệu tiền vốn. Biết cửa hàng đó đã lãi 15%, tính số tiền lãi.

Bài 3: Một trường có 1030 học sinh. Số học sinh nam chiếm 40% học sinh toàn toàn trường. Tìm số học sinh nữ.

Bài 4: Một tấm vải sau khi giặt xong bị co mất 2% so với chiều dài ban đầu. Giặt xong tấm vải chỉ còn 23,5m. Hỏi trước khi gặt tấm vải dài bao nhiêu mét?

Bài 5: Một vườn cây ăn quả có tát cả 1200 cây. Trong đó có 25% là số cây bưởi, 15% là số cây nhãn. Còn lại là số cây xoài. Tính số cây mỗi loại.

Bài 6: Một cửa hàng bán được 420kg gạo và số gạo đó bằng 10,5% tổng số gạo của cửa hàng trước khi bán. Hỏi trước khi bán cửa hàng đó có bao nhiêu tấn gạo?

Bài 7: Lượng nước trong hạt tươi là 20%. Có 200 kg hạt tươi sau khi phơi khô nhẹ đi 30 kg. Tính tỉ số phần trăm nước trong hạt đã phơi khô?

Bài 8: Một lớp có 25% học sinh giỏi, 55% học sinh khá còn lại là học sinh trung bình. Tính số học sinh của lớp đó biết số học sinh trung bình là 5 bạn?

Bài 9: Khi trả bài kiểm tra toán của lớp 5A, cô giáo nói: “Số điểm 10 chiếm 25%, số điểm 9 ít hơn 5%”. Biết rằng có tất cả 18 điểm 9 và 10. Hỏi lớp 5A có bao nhiêu bạn?

Bài 10: Một chiếc xe đạp giá 1 700 000 đồng, nay hạ giá 15%. Hỏi giá chiếc xe đạp bây giờ là bao nhiêu?

Bài 11: Lãi suất tiết kiệm là 0,5% một tháng. Môt người gửi tiết kiệm 5000 000 đồng. Hỏi sau một tháng cả số tiền gửi và số tiền lãi là bao nhiêu ?

Bài 12: Một xưởng may đã dùng 345m vải để may quần áo, trong đó số vải may quần chiếm 40%. Hỏi số vải may áo là bao nhiêu mét ?

Bài 13: Một người bán 120kg gạo, trong đó có 35% là gạo nếp. Hỏi người đó bán được bao nhiêu ki – lô – gam gạo nếp ?

Bài 14: Một mảnh vườn hình chữ nhật có chiều dài 18m và chiều rộng 15m. người ta dành 20% diện tích mảnh đất để làm nhà. Tính diện tích phần đất làm nhà.

Bài 15: Khối lớp Năm của một trường tiểu học có 150 học sinh, trong đó có 52% là học sinh gái. Hỏi khối lớp Năm của trường đó có bao nhiêu học sinh trai ?

Bài 16: Số học sinh nữ của một trường là 420 em và chiếm 52,5% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh ?

Bài 17: Năm vừa qua một nhà máy chế tạo được 1590 ô tô. Tính ra nhà máy đã đạt 120% kế hoạch. Hỏi theo kế hoạch, nhà máy dự định sản xuất bao nhiêu ô tô ?

Bài 18: số học sinh khá giỏi của trường Cát Linh là 552 em, chiếm 92% số học sinh toàn trường. Hỏi trường Cát Linh có bao nhiêu học sinh ?

Bài 19: Kiểm tra sản phẩm của một xưởng may, người ta thấy có 732 sản phẩm đạt chuẩn, chiếm 91,5% tổng số sản phẩm. tính tổng số sản phẩm .

Bài 20: Một tổ sản xuất được 1200 sản phẩm, trong đó anh Ba làm được 126 sản phẩm. Hỏi anh Ba làm được bao nhiêu phần trăm số sản phẩm của tổ ?

Bài 21: Một cửa hàng đã bán được 420kg gạo và số gạo đó bằng 10,5% tổng số gạo của cửa hàng trước khi bán. Hỏi trước khi bán cửa hàng đó có bao nhiêu tấn gạo ?

Bài 22: Một máy bơm trong ba ngày hút hết nước ở hồ. Ngày thứ nhất máy bơm đó hút được 35% lượng nước trong hồ, ngày thứ hai hút được 40% lượng nước trong hồ. Hỏi ngày thứ ba máy bơm đó hút được bao nhiêu phần trăm lượng nước trong hồ ?

Bài 23: Cửa hàng bán một máy tính với giá 6 750 000 đồng. Tiền vốn để mua máy tính đó là 6000 000 đồng. Hỏi khi bán một máy tính, cửa hàng được lãi bao nhiêu phần trăm ?

Bài 24: Lớp 5B có 32 học sinh, trong đó có 24 học sinh thích tập bơi. Hỏi số học sinh thích tập bơi chiếm bao nhiêu phần trăm số học sinh lớp 5B ?

Bài 25: Một mảnh đất hình chữ nhật có chiều dài 15m, chiều rộng 12m. Người ta dành 30% diện tích mảnh đất để làm nhà. Tính diện tích phần đất làm nhà.

Bài 26: Số học sinh giỏi của một trường tiểu học là 64 em và chiếm 12,8% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh ?

Bài 27: Kiểm tra sản phẩm của một nhà máy, người ta thấy có 44 sản phẩm không đạt chuẩn và chiếm 5,5 tổng số sản phẩm. Tính tổng số sản phẩm .

Bài 28: Hai người làm được 1200 sản phẩm, trong đó người thứ nhất làm được 546 sản phẩm. Hỏi số sản phẩm của người đó chiếm bao nhiêu phần trăm tổng số sản phẩm của cả hai người ?

Bài 29: Một cửa hàng bỏ ra 5000 000 đồng tiền vốn và đã lãi 12%. Tính số tiền lãi.

Bài 30: Một cửa hàng đã bán được 123,5 lít nước mắm và bằng 9,5% số nước mắm của cửa hàng có trước khi bán. Hỏi trước khi bán cửa hàng có bao nhiêu lít nước mắm ?

Bài 31: Lớp 5A có 46 học sinh. Tỉ số phần trăm giữa số học sinh nam và số học sinh nữ lớp đó là 100%. Lớp đó có bao nhiêu học sinh nam? Bao nhiêu học sinh nữ?

Bài 32: Giá bán 1kg gạo hôm qua là 16000 đồng. Hôm nay giá gạo giảm 10%. Hỏi hôm nay mua 10kg gạo phải trả bao nhiêu tiền?

Bài 33: Tăng mỗi cạnh của hình chữ nhật thêm 20% số đo của nó thì diện tích hình chữ nhật tăng thêm bao nhiêu phần trăm?

Bài 34: Số gạo tẻ trong kho bằng 120% số gạo nếp. Hỏi phải bán bao nhiêu phần trăm số gạo tẻ để số gạo còn lại của hai loại gạo bằng nhau.

Bài 35: Lãi suất tiết kiệm là 0,65%/tháng. Để sau một tháng nhận được tiền lãi là 832000 đồng thì khách hàng phải gửi số tiền gốc là bao nhiêu?

Bài 36: Một cửa hàng bán một chiếc ti vi giá 9600000 đồng, như vậy lãi 20% so với giá nhập chiếc ti vi đó. Hỏi cửa hàng đã nhập chiếc ti vi đó giá bao nhiêu?

Bài 37. Diện tích thửa ruộng thứ nhất bằng 5/6 diện tích thửa ruộng thứ hai. Hỏi tỉ số phần trăm giữa diện tích thửa ruộng thứ hai và thửa ruộng thứ nhất là bao nhiêu?

Bài 38: Một hình chữ nhật có chiều dài 48cm, chiều rộng 30cm. Tính tỉ số phần trăm của chiều dài so với chiều rộng.

Bài 39: Lớp 5A có 45 học sinh. Số học sinh nữ chiếm 60% số học sinh cả lớp. Hỏi số học sinh nam lớp đó là bao nhiêu em?

Bài 40: Tăng chiều dài 20% số đo của nó, đồng thời giảm chiều rộng 20% số đo của nó thì diện tích hình chữ nhật đó thay đổi thế nào?

Bài 41: Lớp 5A có 45 học sinh trong đó có 18 học sinh nữ. Tính tỉ số phần trăm của số học sinh nam so với số học sinh nữ.

Bài 42: Một người bán chiếc quạt với giá 375000 đồng thì được lãi 12% so với giá bán. Hỏi để lãi 15% so với giá gốc thì phải bán chiếc quạt đó giá bao nhiêu?

Bài 43: Lớp 5A có 45 học sinh, trong đó có 18 học sinh nam. Hỏi số học sinh nữ bằng bao nhiêu phần trăm số học sinh nam?

Bài 44: Một người bán một món hàng với giá 407000 đồng thì được lãi 10% so với giá gốc. Hỏi để lãi 15% so với giá gốc thì người ta phải bán món hàng đó với giá bao nhiêu?

Bài 45: Phải đổ thêm bao nhiêu gam muối vào một bình đựng 300g dung dịch 2% muối để nhận được một bình đựng dung dịch 4% muối.

Bài 46: Sau khi giảm giá 25% thì giá một chiếc xe đạp là 757500 đồng. Hỏi ban đầu giá một chiếc xe đạp là bao nhiêu?

Bài 47: Một cửa hàng bán lương thực đã bán được 20% số gạo trong kho. Hỏi phải nhập thêm bao nhiêu phần trăm số gạo còn lại để trong kho vẫn có số gạo như lúc đầu có?

Bài 48: Một cửa hàng định giá mua bằng 75% giá bán. Hỏi nếu cửa hàng mua một mặt hàng với giá 4500000 đồng thì sẽ bán mặt hàng đó với giá bao nhiêu?

Bài 49: Một hình tam giác có cạnh đáy bằng chiều dài hình chữ nhật, chiều cao bằng 1/2 chiều rộng hình chữ nhật đó. Hỏi diện tích hình tam giác bằng bao nhiêu phần trăm diện tích hình chữ nhật?

Bài 50: Một cửa hàng niêm yết giá bán một chiếc ti vi là 13400000 đồng. Nếu bán chiếc ti vi này bằng 50% giá niêm yết thì lãi 25% so với tiền vốn. Hỏi phải bán chiếc ti vi đó với giá bao nhiêu thì được lãi 50% so với tiền vốn?

Bài 51: Một cửa hàng đã bán được 420kg gạo và số gạo đó bằng 10,5% tổng số gạo của cửa hàng trước khi bán. Hỏi trước khi bán cửa hàng đó có bao nhiêu tấn gạo ?

Bài 52: Một máy bơm trong ba ngày hút hết nước ở hồ. Ngày thứ nhất máy bơm đó hút được 35% lượng nước trong hồ, ngày thứ hai hút được 40% lượng nước trong hồ. Hỏi ngày thứ ba máy bơm đó hút được bao nhiêu phần trăm lượng nước trong hồ ?

Bài 53: Cửa hàng bán một máy tính với giá 6 750 000 đồng. Tiền vốn để mua máy tính đó là 6000 000 đồng. Hỏi khi bán một máy tính, cửa hàng được lãi bao nhiêu phần trăm?

Bài 54: Lớp 5B có 32 học sinh, trong đó có 24 học sinh thích tập bơi. Hỏi số học sinh thích tập bơi chiếm bao nhiêu phần trăm số học sinh lớp 5B ?

Bài 55: Một mảnh đất hình chữ nhật có chiều dài 15m, chiều rộng 12m. Người ta dành 30% diện tích mảnh đất để làm nhà. Tính diện tích phần đất làm nhà.

Bài 56: Số học sinh giỏi của một trường tiểu học là 64 em và chiếm 12,8% số học sinh toàn trường. Hỏi trường đó có bao nhiêu học sinh ?

Bài 57: Kiểm tra sản phẩm của một nhà máy, người ta thấy có 44 sản phẩm không đạt chuẩn và chiếm 5,5 tổng số sản phẩm. Tính tổng số sản phẩm .

Bài 58: Hai người làm được 1200 sản phẩm, trong đó người thứ nhất làm được 546 sản phẩm. Hỏi số sản phẩm của người đó chiếm bao nhiêu phần trăm tổng số sản phẩm của cả hai người ?

Bài 59: Một cửa hàng bỏ ra 5000 000 đồng tiền vốn và đã lãi 12%. Tính số tiền lãi.

Bài 60: Một cửa hàng đã bán được 123,5 lít nước mắm và bằng 9,5% số nước mắm của cửa hàng có trước khi bán. Hỏi trước khi bán cửa hàng có bao nhiêu lít nước mắm ?

Bài 61: Một cửa hàng có 500kg gạo. Buổi sáng người ta bán được 45% số gạo đó, buổi chiều bán được 80% số gạo còn lại. Hỏi cả hai lần, cửa hàng bán được bao nhiêu ki – lô – gam gạo ?

Bài 62: Một lớp học có 18 nữ và 12 nam. Hỏi số học sinh nam chiếm bao nhiêu phần trăm số học sinh cả lớp ?

Bài 63: Khối Năm của trường tiểu học Ba Đình có 500 học sinh, trong đó có 215 bạn nữ. Tính tỉ số phần trăm học sinh nam và số học sinh toàn trường.

Bài 64: Một người bỏ ra 9 500 000 đồng tiền vốn để mua hàng. Sau khi bán hết hàng, họ thu được 12 000 000 đồng. Hỏi :

a) Tiền bán bằng bao nhiêu phần trăm tiền vốn ?

b) Tiền lãi bằng bao nhiêu phần trăm tiền vốn ?

Bài 65: Một người bỏ ra 450 000 đồng mua hàng. Sau khi bán hết hàng người đó thu được 500 000 đồng. Hỏi :

a) Tiền lãi bằng bao nhiêu phần trăm tiền vốn ?

b) Tiền lãi bằng bao nhiêu phần trăm tiền bán ?

Bài 66: Lớp 5A có 48 học sinh. Số học sinh học lực khá chiếm 75% số học sinh cả lớp. Hỏi lớp 5A có bao nhiêu bạn học lực khá, bao nhiêu bạn học lực không phải là loại khá?

Bài 67: Một cửa hàng mua một số hàng giá trị 7,5 triệu đồng về bán. Bán hết hàng họ tính ra được lãi 8,5% giá trị mua. Hỏi cửa hàng bán số hàng đó được bao nhiêu tiền?

Bài 68: Một cửa hàng buổi sáng bán được 10% số gạo, buổi chiều bán được 15% số gạo. Hỏi cửa hàng đó còn lại bao nhiêu ki – lô – gam gạo ? biết cửa hàng có 500kg gạo.

Bài 69: Một cửa hàng đã bán được 123,5kg gạo bằng 9,5% tổng số gạo cửa hàng trước khi bán. Hỏi trước khi bán cửa hàng có bao nhiêu ki – lô – gam gạo ?

Bài 70: Tháng vừa qua, xí nghiệp may được 8970 bộ quần áo. Tính ra xí nghiệp đạt 115% kế hoạch. Hỏi xí nghiệp đã may nhiều hơn so với dự định bao nhiêu bộ quần áo ?

B. Lý thuyết về tỉ số phần trăm

1. Tỉ số phần trăm là gì?

Tỷ số của hai số là thương của phép chia số a cho số b với b khác 0, được viết dưới dạng a / b hoặc a : b.

Tỷ số phần trăm chính là tỉ số của hai số mà ở đó ta sẽ quy mẫu số của tỉ số về số 100. Tỷ số phần trăm thường được sử dụng để biểu thị độ lớn tương đối của một lượng này so với lượng khác. Ví dụ: 2/100 = 2%, 35/100 = 35%

Ký hiệu thường dùng là “%” – ký hiệu phần trăm. Ví dụ: 50% (đọc là “năm mươi phần trăm”) tương đương với 50/100, nói cách khác là 0,5.

2. Tỉ số phần trăm có ý nghĩa gì?

Trong toán học, phần trăm là tỉ số thể hiện dưới dạng phân số có mẫu số là 100. Tương tự, một số hệ thống diễn đạt phân số có mẫu số là 1000 được gọi là hệ thống phần nghìn. Phần trăm được sử dụng để biểu thị độ lớn tương đối của một lượng so với một lượng khác. Cụ thể đại lượng thứ nhất thường thể hiện phần tương ứng hoặc phần thay đổi so với đại lượng thứ hai.

3. Công thức tính tỉ số phần trăm

- Cách tính tỉ số phần trăm của 1 số

Trong toán học, phần trăm là tỷ lệ được hiển thị dưới dạng phân số với mẫu số luôn luôn bằng 100. Ngoài ra, phần trăm còn được biểu diễn ở dạng khác bằng cách dùng ký hiệu % mà bạn thường gặp như 1%, 5%, 10%,… Điều đặc biệt là phần trăm không có đơn vị đo lường.

Bạn sẽ thường thấy rằng phần trăm được dùng để chỉ ra mức độ (hay độ lớn) của một lượng này so với một lượng kia. Ví dụ, một lớp học có 30 học sinh, trong đó có 15 học sinh là nữ thì ta có thể nói rằng số học sinh nữ chiếm tỉ lệ 50% trong tổng số học sinh của lớp học đó.

Để hiểu rõ hơn về tỷ lệ phần trăm, dưới đây là cách tính phần trăm của 1 số:

• Tính phần trăm khi biết tổng thể với a là một số, b là tổng thể, ta tính như sau: (a/b)*100 (%).

Ví dụ, một một lớp học có 20 học sinh, trong đó có 5 học sinh là nữ. Thì ta có, 20 học sinh là tổng thể, 5 học sinh nữ là số bạn cần so sánh. Ta có phép tính như sau: (5/20)*100(%).

• Tính phần trăm khi chưa biết tổng thể với a là một số, b là một số, ta tính như sau: a/(a+b))*100 hay b/(a+b))*100 (%).

Ví dụ, một giỏ trái cây gồm 10 trái cam và 5 trái táo, để tính được phần trăm trái cam có trong giỏ trái cây ấy thì ta cần tính tổng thể của giỏ trái cây đó trước rồi thực hiện cách tính phần trăm như trên. Lúc này, giỏ trái cây gồm 25 trái, ta có phép tính như sau: (10/(10+5))*100.

Tương tự như vậy, để tính phần trăm trái táo có trong giỏ trái cây ấy thì ta có phép tính như sau: (5/(10+5))*100 (%) hoặc 100-% trái cam.

- Cách tính phần trăm của 2 số

Cách tính phần trăm của 2 số a, b đó chính là lấy số a đem chia số b và nhân cho 100. Chúng ta sẽ ghi ký hiệu phần trăm (%) ở đằng sau kết quả mình nhận được. Cụ thể là:

(a : b) x 100 = a/b x 100 (%)

Ví dụ: 1 trận bóng đá có 22 cầu thủ. Trong số đó, có 8 người da vàng và 14 người da trắng. Hỏi tỉ số các cầu thủ da trắng so với tổng cộng là bao nhiêu?

Lời giải:

Tỉ số các cầu thủ da trắng so với toàn bộ cầu thủ trên sân là:

(14 : 22) x 100 = 63, 63%

- Cách tính phần trăm của một tổng

Đây là cách tính phần trăm được dùng nhiều nhất trong tất cả. Khi tính phần trăm 1 tổng, bạn sẽ biết đại lượng này chiếm bao nhiêu phần trong tổng chung.

Cách tính phần trăm A so với tổng (A+B): A/(A+B)*100

- Cách tính phần trăm tăng trưởng so sánh

Một khái niệm vô cùng quen thuộc trong lĩnh vực kinh tế mà bạn đã nghe qua đó là phần trăm tăng trưởng. Vậy phần trăm tăng trưởng là gì? Là mức độ tăng trưởng hay phát triển mà một doanh nghiệp, công ty hay thậm chí là nền kinh tế đó tăng/giảm nhanh/chậm so với những quý/kỳ/năm trước đó.

Công thức để tính phần trăm tăng trưởng: % tăng trưởng=(năm cần tính – năm trước)/năm trước*100

- Cách tính phần trăm hoàn thành công việc

Sẽ có đôi khi ta cũng cần đến cách tính phần trăm để đánh giá mức độ hoàn thành công việc. Giờ đây, công thức này còn được nâng cấp lên để tính tỷ lệ hoàn thành công việc theo dự kiến giúp cho việc hoạch định kế hoạch được tốt hơn,…

Công thức tính phần trăm hoàn thành công việc: (số công việc đã hoàn thành x/ số công việc phải hoàn thành y)*100

- Công thức tìm một số khi biết phần trăm của số đó

Muốn tìm một số khi biết phần trăm của số đó ta lấy số đó chia cho số phần trăm rồi nhân với 100 hoặc lấy giá trị đó nhân với 100 rồi chia cho số phần trăm.

Muốn tìm một số biết b% của số đó là B:

B : b% = B : b x 100

Phương pháp này ngược lại với công thức tính tỷ số phần trăm của một số.