Tailieumoi.vn xin giới thiệu Bài tập Hình học lớp 6 được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 100 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Hình học lớp 6. Mời các bạn đón xem:

Bài tập Hình học lớp 6

A. Bài tập Hình học lớp 6

1. Bài tập về hình tam giác đều, hình vuông, lục giác đều

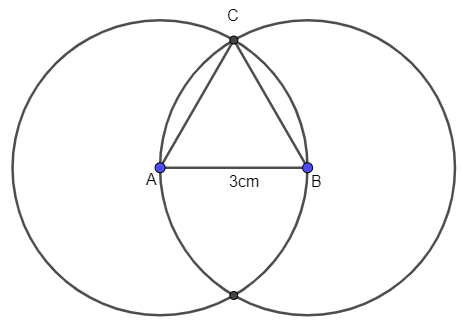
Bài 1. Vẽ tam giác đều cạnh 3cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 3cm.

Bước 2. Dùng compa vẽ đường tròn tâm A bán kính 3cm và đường tròn tâm B bán kính 3 cm.

Bước 3. Hai đường tròn này giao nhau tại C. Nối A với C, B với C ta được tam giác ABC đều.

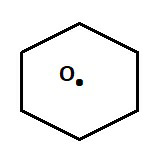
Bài 2. Người ta muốn đặt một trạm biến áp để đưa điện về sáu ngôi nhà. Phải đặt trạm biến áp ở đâu để khoảng cách từ trạm biến áp đến sáu ngôi nhà đều bằng nhau, biết rằng sáu ngôi nhà ở vị trí sáu đỉnh của lục giác đều.

Lời giải

Phải đặt trạm biến áp ở tâm O hình lục giác đều tạo bởi sáu ngôi nhà.

Vì độ dài các đường chéo chính của hình lục giác đều bằng nhau, mà O là trung điểm của các đường chéo đó nên khoảng cách từ tâm O đến các đỉnh của lục giác đều là bằng nhau hay nếu đặt trạm biến áp ở O thì khoảng cách từ trạm biến áp đến sáu ngôi nhà đều bằng nhau.

2. Bài tập về hình chữ nhật, hình thoi, hình bình hành, hình thang cân

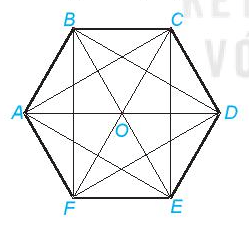
Bài 1. Hãy kể tên các hình thang cân, hình chữ nhật, hình thoi có trong lục giác đều sau: 

Lời giải

Trong hình đã cho:

- Hình thang cân: ABCD, BCDE, DEFA, EFAB.

- Hình chữ nhật: ACDF, BCEF.

- Hình thoi: ABOF, ABCO, BCDO, DEFO, CDEO, EFAO.

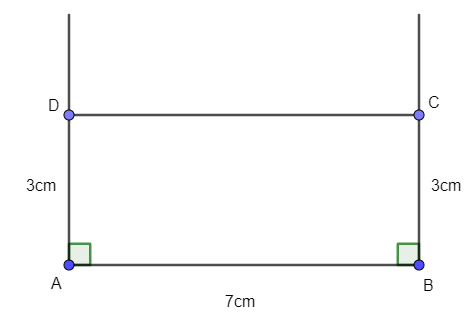
Bài 2. Vẽ hình chữ nhật có một cạnh dài 7cm, một cạnh 3cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 7cm.

Bước 2. Dựng đường thẳng vuông góc với AB tại A. Trên đường thẳng này lấy điểm D sao cho AD = 3cm.

Bước 3. Dựng đường thẳng vuông góc với AB tại B. Trên đường thẳng này lấy điểm C sao cho BC = 3cm.

Bước 4. Nối C với D ta được hình chữ nhật có AB = 7cm, AD = 3cm.

3. Bài tập tính chu vi một số hình tứ giác đã học

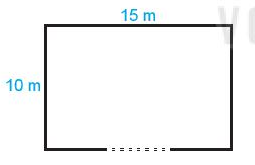
Bài 1. Một khu vườn hình chữ nhật có chiều dài 15m, chiều rộng 10m như hình dưới, cổng vào có độ rộng bằng 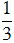  chiều dài, phần còn lại là hàng rào. Hỏi hàng rào của khu vườn dài bao nhiêu mét?

Lời giải

Độ rộng của cửa là: 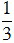 .15 = 5(m)  .

Chu vi hình chữ nhật là: 2.(10 + 15) = 2.25 = 50 (m)

Độ dài của hàng rào của khu vườn hình chữ nhật: 50 – 5 = 45 (m).

Bài 2. Một ngôi nhà có bãi có bảo quanh như hình bên.

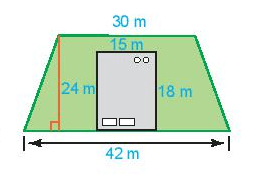
a) Hãy tính diện tích của bãi cỏ.

b) Nếu một túi hạt giống cỏ gieo vừa đủ trên 54m² đất, thì cần bao nhiêu túi hạt giống để gieo vừa hết bãi cỏ?

Lời giải

Diện tích cả bãi cỏ và khu đất làm nhà là: 

(30 + 42).24:2 = 864 (m²).

Diện tích khu đất làm nhà là: 

15.18 = 270 (m²).

a) Diện tích cả bãi cỏ là:

864 – 270 = 594 (m²).

Vậy diện tích bãi cỏ là 594 m².

b) Để gieo hết bãi cỏ thì cần số túi hạt giống là: 594:54 = 11 (túi).

Vậy cần tất cả 11 túi hạt giống để gieo hết bãi cỏ.

4. Bài tập về hình có tâm đối xứng, trục đối xứng

Bài 1. Trong các hình bên, em hãy chỉ ra:

a) Những hình có tâm đối xứng;

b) Những hình có trục đối xứng.

Lời giải

a) Những hình có tâm đối xứng là: cánh quạt.

b) Những hình có trục đối xứng là: tam giác đều, trái tim và cánh diều.

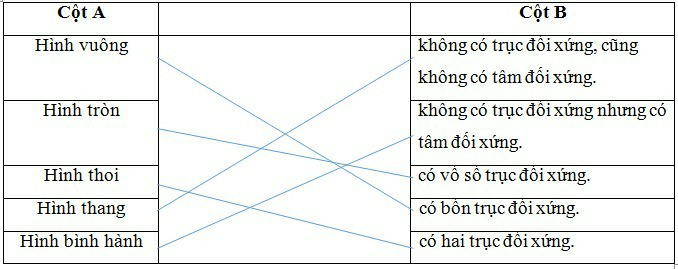
Bài 2. Nối cột A với cột B để được một phát biểu đúng.

 

Cột A		Cột B
Hình vuông		không có trục đối xứng, cũng không có tâm đối xứng.
Hình tròn		không có trục đối xứng nhưng có tâm đối xứng.
Hình thoi		có vố số trục đối xứng.
Hình thang		có bốn trục đối xứng.
Hình bình hành		có hai trục đối xứng.

Lời giải

Hình vuông là hình có 4 trục đối xứng là hai đường chéo và hai đường nối trung điểm của các cặp cạnh đối diện.

Hình tròn là hình có vô số trục đối xứng là các đường thẳng đi qua tâm.

Hình thoi là hình có hai trục đối xứng là hai đường chéo.

Hình thang không có trục đối xứng và cũng có tâm đối xứng.

Hình bình hành là hình không có trục đối xứng và có tâm đối xứng.

Ta hoàn thành bảng ghép cột như sau:

5. Bài tập Hình học cơ bản

Bài 1: Cho hình vẽ:

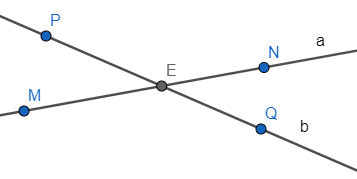
a) Điểm nào thuộc đường thẳng a (trả lời và viết kí hiệu)?

b) Điểm nào thuộc đường thẳng b (trả lời và viết kí hiệu)?

c) Điểm nào thuộc đường thẳng a nhưng không thuộc đường thẳng b (trả lời và viết kí hiệu)?

Lời giải: 

a) Điểm thuộc đường thẳng a là điểm M; E; N

Kí hiệu: M ∈ a; N ∈ a; E ∈ a

b) Điểm thuộc đường thẳng b là điểm P; Q; E

Kí hiệu: P ∈ b; Q ∈ b; E ∈ b.

c) Điểm thuộc đường thẳng a nhưng không thuộc đường thẳng b là điểm M và điểm N

Kí hiệu: M ∈ a; N ∈ a và M ∉ b; N ∉ b.

Bài 2: Kể tên các đoạn thẳng có trong hình sau: 

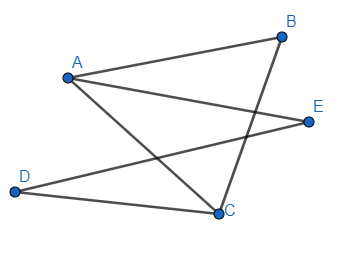
Lời giải:

Các đoạn thẳng có trong hình là: AB; AE; AC; BC; CD; DE.

Bài 3: Kể tên các góc có trong hình:

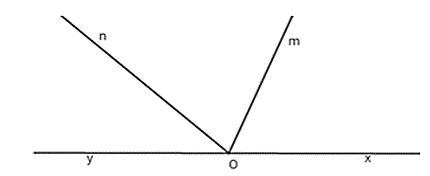
Lời giải:

Các góc có trong hình là: ∠xOm;∠xOn;∠xOy;∠mOn;∠mOy;∠nOy

Bài 4: Cho hai tia đối nhau Ox; Ox’. Trên tia Ox vẽ điểm A sao cho OA = 2cm. Trên tia Ox’ vẽ điểm B sao cho OB = 2cm. Hỏi O có là trung điểm của đoạn thẳng AB không? Vì sao?

Lời giải: 

Vì A nằm trên tia Ox và B nằm trên tia Ox’ mà Ox và Ox’ đối nhau nên O nằm giữa A và B.

Mà OA = OB = 2cm nên O là trung điểm của đoạn thẳng AB.

Bài 5: Trên tia Ox vẽ hai điểm A và B sao cho OA = 3cm; OB = 8cm

a) Tính độ dài đoạn thẳng AB.

b) Gọi C là trung điểm của OB. Tính độ dài AC.

Lời giải:

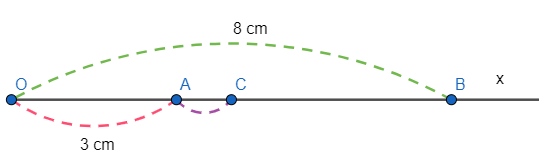
a) A, B thuộc tia Ox mà OA < OB nên A nằm giữa hai điểm O và B, ta có: 

OA + AB = OB

Thay số:

3 + AB = 8

AB = 8 – 5

AB = 3cm

b) Vì C là trung điểm của OB nên OC = BC = 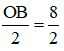  = 4cm.

Hai điểm A và C cùng nằm trên tia Ox mà OA < OC nên A nằm giữa O và C

Ta có: OA + AC = OC

Thay số :

3 + AC = 4

AC = 4 – 3

AC = 1cm

Bài 6: Vẽ hai đường thẳng xx’ và yy’ cắt nhau tại điểm M sao cho góc xMy có số đo bằng 60^o. Trên tia My’ lấy một điểm N khác M rồi vẽ đường thẳng aa’ đi qua N và song song với xx’.

a) Kể tên tất cả 8 góc có đỉnh M hoặc N, không kể các góc bẹt.

b) Dùng thước đo góc để đo 8 góc đã nêu trong câu a rồi sắp xếp chúng thành 2 nhóm, mỗi nhóm gồm các góc bằng nhau.

Lời giải: 

* Cách vẽ:

- Vẽ đường thẳng xx’ bất kỳ.

- Lấy điểm M thuộc đường thẳng xx’.

- Vẽ đường thẳng yy’ đi qua M thỏa mãn ∠xMy = 60^o.

- Trên tia My’ lấy điểm N (N khác M).

- Qua N kẻ đường thẳng aa’ song song với đường thẳng xx’.

* Ta có hình vẽ:

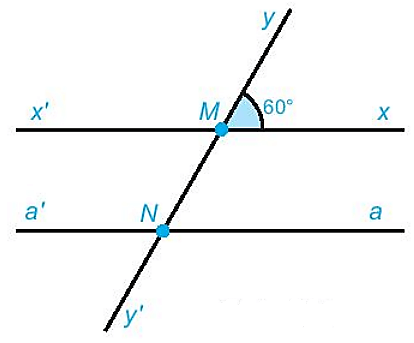
a) Các góc có đỉnh M (không kể góc bẹt) là: 

∠xMy;∠x'My;∠xMy';∠x'My'

Các góc có đỉnh N (không kể góc bẹt) là: 

∠aNy;∠aNy';∠a'Ny;∠a'Ny'

Vậy 8 góc có đỉnh M hoặc N (không kể các góc bẹt) là 

∠xMy;∠x'My;∠xMy';∠x'My';∠aNy;∠aNy';∠a'Ny;∠a'Ny'

b) Đo 8 góc đã nêu ở câu a, ta được:

∠xMy = ∠x'My' = ∠aNy = ∠a'Ny' = 60^o

∠x'My = ∠xMy' = ∠a'Ny = ∠aNy' = 120^o

Vậy 8 góc đã nêu ở câu a có thể xếp vào hai nhóm các góc bằng nhau như sau:

Nhóm 1: ∠xMy;∠x'My';∠aNy;∠a'Ny

Nhóm 2: ∠x'My;∠xMy';∠a'Ny;∠aNy'

B. Lý thuyết Hình học lớp 6

I. Hình học phẳng

1. Hình tam giác đều

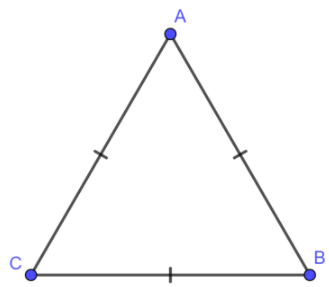
Trong tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng 60⁰C.

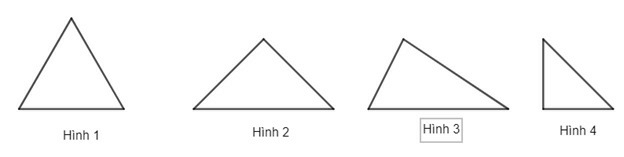
Ví dụ 1. Trong các hình dưới đây, hình nào là tam giác đều:

Lời giải

Sử dụng thước thẳng đo lần lượt các cạnh của từng hình, ta nhận thấy:

Hình 1 có độ dài các cạnh bằng nhau. Do đó HÌnh 1 là tam giác đều.

2. Hình vuông

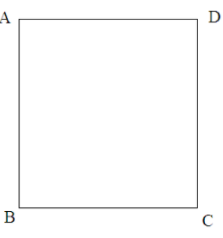
Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 90⁰.

- Hai đường chéo bằng nhau.

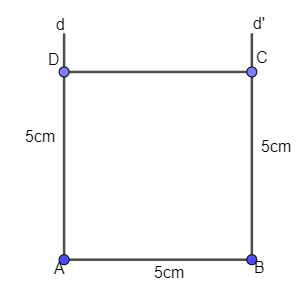
Ví dụ 2. Vẽ hình vuông ABCD có cạnh bằng 5cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 5cm;

Bước 2. Qua A dựng đường thẳng d vuông góc với AB, qua B dựng đường thẳng d’ vuông góc với AB.

Bước 3. Trên đường thẳng d lấy điểm D sao cho AD = 5cm, trên d’ lấy điểm C sao cho BC = 5cm.

Bước 4. Nối D với C ta được hình vuông ABCD.

Công thức:

Hình vuông cạnh a:

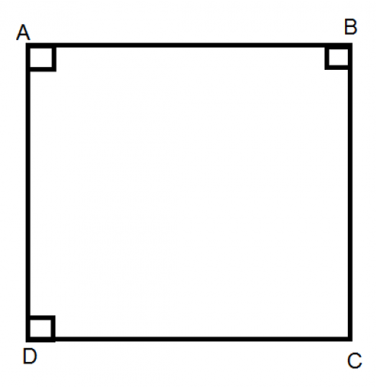
Chu vi: C = 4a.

Diện tích: S = a².

3. Hình lục giác đều

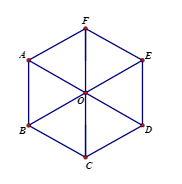
Hình lục giác đều có:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau, mỗi góc bằng 120⁰.

- Ba đường chéo chính bằng nhau.

Ví dụ 3. Hãy quan sát hình vẽ:

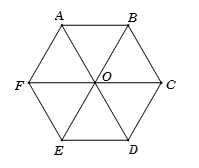
a) Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.

b) Hãy so sánh độ dài các đường chéo chính với nhau.

Lời giải

a) Các đường chéo chính của hình lục giác đều ABCDEF là: AD, BE, CF.

b) Sau khi đo độ dài ta thấy AD = BE = CF = 2,1 cm.

4. Hình chữ nhật

Trong hình chữ nhật có:

- Bốn góc bằng nhau và bằng 90⁰C.

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo bằng nhau.

Hình chữ nhật có chiều dài là a, chiều rộng là b:

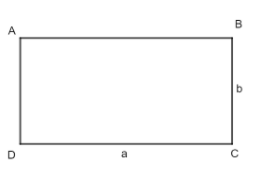
Chu vi: C = 2(a + b).

Diện tích: S = a.b.

Ví dụ 1. Lấy ví dụ về các hình có dạng hình chữ nhật trong thực tiễn.

Lời giải

Mặt bàn, Mặt bảng, cửa ra vào, cửa sổ, …

5. Hình thoi

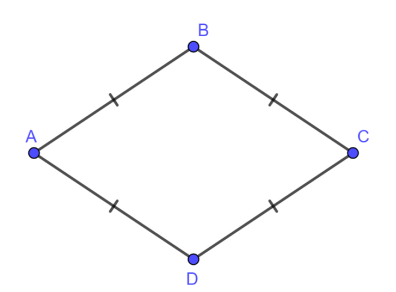
Trong hình thoi :

- Bốn cạnh bằng nhau.

- Hai đường chéo vuông góc với nhau.

- Các cặp góc đối bằng nhau.

Hình thoi:

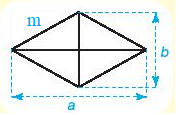
Chu vi: C = 4.m.

Diện tích: S = 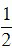ab .

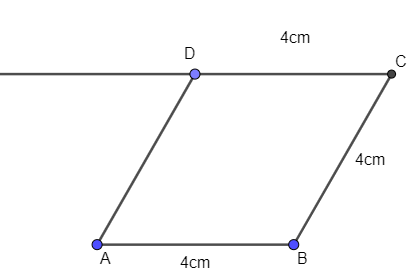
Ví dụ 2. Vẽ hình thoi cạnh 4cm.

Lời giải

Bước 1. Vẽ đoạn thẳng AB = 4cm.

Bước 2. Vẽ đoạn thẳng BC = 4cm (điểm C khác điểm A).

Bước 3. Qua điểm C vẽ đường thẳng song song với AB. Trên đường thẳng này lấy điểm D sao cho CD = 4cm.

Bước 4. Nối D với A ta được hình thoi ABCD.

6. Hình bình hành

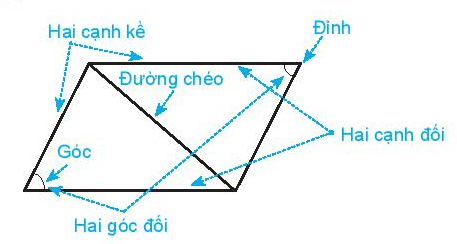
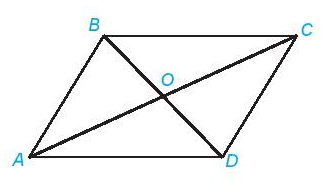
Trong hình bình hành:

- Các cặp cạnh đối bằng nhau.

- Hai đường chéo cắt nhau tại trung điểm của mỗi đường.

- Các cặp cạnh đối song song.

- Các cặp góc đối bằng nhau.

Hình bình hành: 

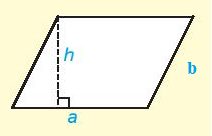
Chu vi: C = 2(a + b).

Diện tích: S = a.h.

Ví dụ 3. Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại điểm I. Sử dụng compa hoặc thước thẳng kiểm tra xem điểm I có là trung điểm của hai đường chéo không?

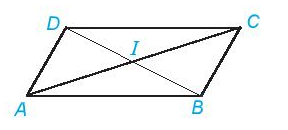
Lời giải

+) Nếu sử dụng compa:

- Đầu tiên mở một khoảng compa trùng với đoạn IA. Sau đó giữ nguyên khoảng đó đặt vào đoạn IC thấy trùng nhau.

- Tương tự mở compa một khoảng trùng với IB. Sau đó giữ nguyên khoảng đó đặt vào đoạn ID thấy trùng nhau.

Vậy điểm I chính là trung điểm của hai đường chéo.

+) Nếu sử dụng thước thẳng:

Ta sẽ đo độ dài của từng đoạn một, thì thấy IA = IC, IB = IB.

Vậy I chính là trung điểm của hai đường chéo.

7. Hình thang cân

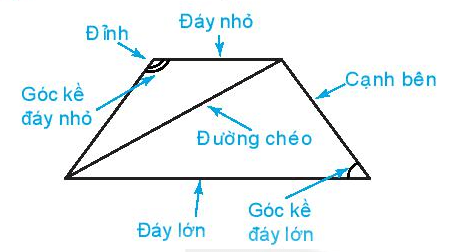
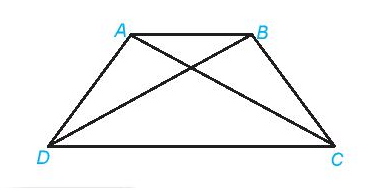
Trong hình thang cân:

- Hai cạnh bên bằng nhau.

- Hai đường chéo bằng nhau.

- Hai cạnh đáy song song với nhau.

- Hai góc kề một đáy bằng nhau.

Hình thang có độ dài hai cạnh đáy là a, b chiều cao h:

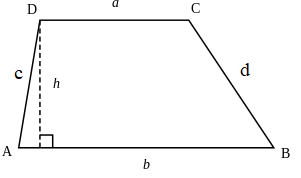
Chu vi: C = a + b + c + d.

Diện tích: S = (a + b).h:2.

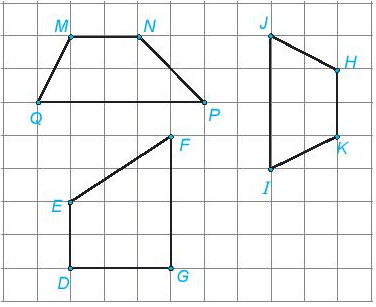
Ví dụ 4. Hình nào trong các hình đã cho là hình thang cân? Hãy cho biết tên hình thang cân đó.

Lời giải

Đầu tiên lấy eke kiểm tra hai cạnh đáy có song song với nhau không.

Tiếp theo lấy thước thẳng đo độ dài hai đường chéo nếu bằng nhau thì là hình thang cân.

Từ kết quả đo, ta thấy các hình trên hình thang cân là HKIJ.

II. Tính đối xứng của hình học phẳng

1. Hình có trục đối xứng trong thực tế

Các hình có một đường thẳng d chia hình đó thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau. Những hình như thế được gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.

2. Trục đối xứng của một số hình phẳng

Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn. Do đó hình tròn có vô số trục đối xứng.

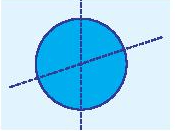
Mỗi đường chéo là một trục đối xứng của hình thoi.

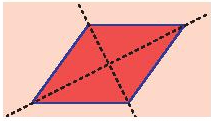
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.

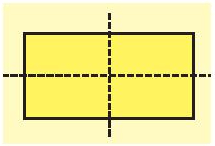
Hình vuông có 4 trục đối xứng bao gồm: Hai đường thẳng đi qua trung điểm hai cạnh đối điện và hai đường chéo.

3. Hình có tâm đối xứng trong thực tế

Mỗi hình có mổ điểm O, mà khi quay hình đó xung quanh điểm O đúng một nửa vòng thì hình thu được “trùng khít” với chính nó ở vị trí ban đầu (trước khi quay).

Những hình như thế được gọi là “hình có tâm đối xứng” và điểm O được gọi là “tâm đối xứng” của hình.

4. Tâm đối xứng của một số hình phẳng

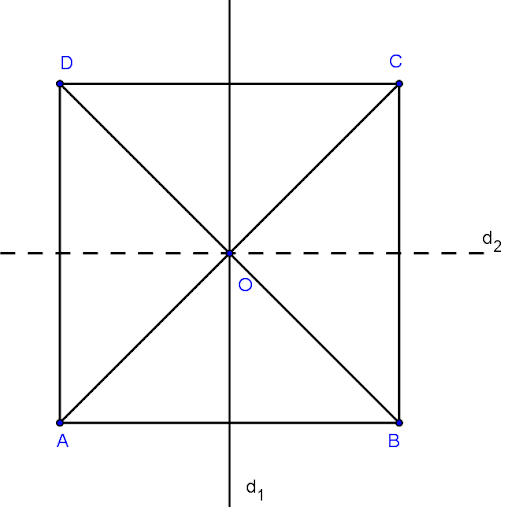
Tâm đối xứng của hình bình hành, hình thoi, hình vuông, hình chữ nhật là giao điểm của hai đường chéo.

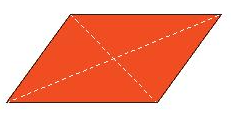
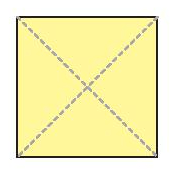
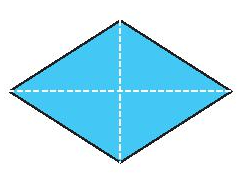
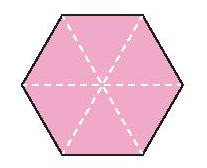
Tâm đối xứng của hình lục giác đều là giao điểm của các đường chéo chính.

III. Hình học cơ bản

1. Điểm thuộc, không thuộc đường thẳng

a) Điểm, đường thẳng

- Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm.

- Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.

- Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.

b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng

- Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.

- Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.

- Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.

c) Đường thẳng đi qua hai điểm phân biệt

- Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt

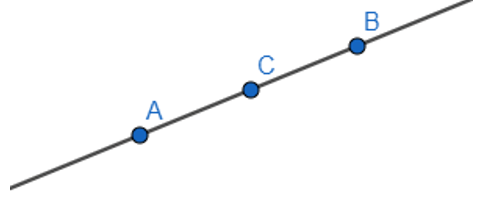
2. Ba điểm thẳng hàng

- Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.

3. Hai đường thẳng song song, cắt nhau, trùng nhau.

- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.

- Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.

- Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.

a và b song song với nhau kí hiệu: a // b	a và b cắt nhau tại điểm E	Đường thẳng AB và đường thẳng BC trùng nhau.

4. Điểm nằm giữa hai điểm

+ Điểm B nằm giữa hai điểm A và C.

+ Hai điểm A và B nằm cùng phía đối với điểm C.

+ Hai điểm A và C nằm khác phía đối với điểm B.

5. Tia

a) Tia

Điểm O trên đường thẳng xy chia đường thẳng xy thành hai phần.

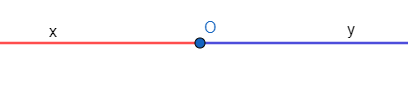
- Hình gồm điểm O và một phần đường thẳng bị chia ra bởi điểm O được gọi là một tia gốc O. Điểm O là gốc của tia.

b) Hai tia đối nhau

- Hai tia đối nhau là hai tia chung gốc và tạo thành một đường thẳng

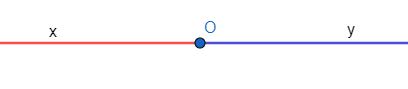
- Hai tia Ox và Oy là gọi là hai tia đối nhau (tia Ox là tia đối của tia Oy và tia Oy là tia đối của tia Ox).

c) Hai tia trùng nhau

- Hai tia trùng nhau là hai tia chung gốc và có thêm ít nhất 1 điểm chung khác điểm gốc

- Khi điểm B thuộc tia Am thì tia Am còn được gọi là tia AB, khi đó tia Am và tia AB được gọi là trùng nhau.

6. Đoạn thẳng

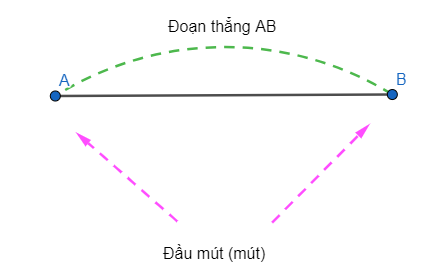
- Đoạn thẳng AB, hay đoạn thẳng BA, là hình gồm 2 điểm A, B cùng với tất cả các điểm nằm giữa A và B.

- A; B là hai đầu mút (mút) của đoạn thẳng AB.

7. Độ dài đoạn thẳng

a) Độ dài đoạn thẳng

- Mỗi đoạn thẳng có một độ dài. Khi chọn một đơn vị độ dài thì độ dài mỗi đoạn thẳng được biểu diễn bởi một số dương (thường viết kèm đơn vị).

- Độ dài đoạn thẳng AB còn gọi là khoảng cách giữa hai điểm A và B. Ta quy ước khoảng cách giữa hai điểm trùng nhau bằng 0 (đơn vị).

- Đơn vị đo độ dài đoạn thẳng: mm; cm; dm; m; km…

b) So sánh độ dài đoạn thẳng

- Hai đoạn thẳng AB và EG có cùng độ dài. Ta viết AB = EG và nói đoạn thẳng AB bằng đoạn thẳng EG.

- Đoạn thẳng AB có độ dài nhỏ nhơn đoạn thẳng CD. Ta viết AB < CD và nói AB ngắn hơn CD hoặc CD > AB và nói CD dài hơn AB.

c) Đo độ dài đoạn thẳng

Để đo độ dài đoạn thẳng ta làm như sau:

Bước 1: Đặt thước trùng với đường thẳng sao cho vạch 0 của thước trùng với một đầu mút của đoạn thẳng.

Bước 2: Quan sát xem đầu mút còn lại trùng với vạch mấy của thước thì số chỉ ở vạch đó chính là độ dài đoạn thẳng.

Chú ý: Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB

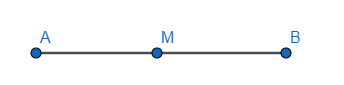
8. Trung điểm của đoạn thẳng

- Nếu điểm I nằm giữa hai điểm A và B sao cho IA = IB thì I gọi là trung điểm của đoạn thẳng AB.

Khi đó:

IA = IB =  .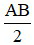

9. Góc

- Góc là hình gồm hai tia chung gốc. Gốc chung của hai tia gọi là đỉnh của góc. Hai tia là hai cạnh của góc.

+ Góc xOy, kí hiệu 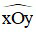 (hoặc ∠xOy ) gồm hai tia chung gốc Ox và Oy.

+ Điểm O là đỉnh của góc xOy. Hai tia Ox; Oy là các cạnh của góc xOy.

+ Góc xOy còn có các cách gọi khác là góc AOB; góc O; góc yOx; góc BOA.

+ Đặt biệt khi Ox và Oy là hai tia đối nhau, ta có góc bẹt xOy.

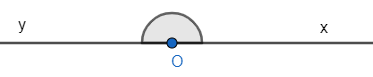
10. Điểm trong của góc

Quan sát hình vẽ:

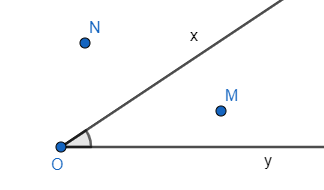
- Ta gọi M là một điểm trong của góc xOy (điểm M nằm trong góc xOy).

- Các điểm nằm trên hai cạnh của góc và các điểm như điểm N không phải là điểm trong góc xOy.

11. Đo góc

- Muốn đo 1 góc xOy, ta đặt thước đo góc sao cho tâm của thước trùng với O, tia Ox đi qua vạch 0. Khi đó tia Oy đi qua vạch chỉ số đo của góc.

12. Các góc đặc biệt

- Góc có số đo bằng 90^o là góc vuông.

- Góc bẹt là góc có số đo bằng 180^o.

- Góc nhỏ hơn góc vuông là góc nhọn.

- Góc lớn hơn góc vuông và nhỏ hơn góc bẹt là góc tù.

Góc vuông	Góc nhọn	Góc tù	Góc bẹt
∠xAy = 90o	0o < ∠xAy < 90o	90o < ∠xAy < 180o	∠xAy = 180o

C. Các dạng bài tập Hình học lớp 6

1. Nhận biết các quan hệ: điểm thuộc, không thuộc đường thẳng; đường thẳng đi qua hai điểm phân biệt; ba điểm thẳng hàng

Phương pháp giải

* Nhận biết điểm thuộc đường thẳng và điểm không thuộc đường thẳng

- Xét xem trên đường thẳng có những điểm nào thì những điểm đó thuộc đường thẳng và đường thẳng đi qua điểm đó.

- Xét xem ngoài đường thẳng có những điểm nào thì những điểm đó không thuộc đường thẳng và đường thẳng không đi qua điểm đó.

* Đường thẳng đi qua hai điểm phân biệt

Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt.

* Nhận biết ba điểm thẳng hàng

- Xét xem nếu ba điểm thẳng hàng thì chúng cùng thuộc một đường thẳng, ba điểm không thẳng hàng thì chúng không cùng thuộc bất kỳ đường thẳng nào.

Ví dụ. Cho hình vẽ sau:

a) Kể tên các đường thẳng.

b) Điểm I nằm trên đường thẳng nào?

c) Điểm K không thuộc đường thẳng nào?

d) Kể tên ba điểm thẳng hàng.

Hướng dẫn giải:

a) Các đường thẳng là: a, b, c, d.

b) Điểm I nằm trên các đường thẳng là: a, b, d.

c) Điểm K không thuộc đường thẳng a, d.

d) Vì ba điểm J, K, L cùng nằm trên đường thẳng c nên ba điểm J, K, L thẳng hàng.

2. Hai đường thẳng cắt nhau, song song, trùng nhau

Phương pháp giải

- Xét xem hai đường thẳng có đúng một điểm chung thì hai đường thẳng đó cắt nhau.

- Xét xem hai đường thẳng không điểm chung thì hai đường thẳng đó song song.

- Xét xem hai đường thẳng nằm “chồng khít” lên nhau thì hai đường thẳng đó trùng nhau.

- Khi nói hai đường thẳng mà không nói gì thêm thì đó là hai đường thẳng phân biệt (tức là không trùng nhau).

Ví dụ. Điền vào chỗ trống:

a) Đường thẳng x và đường thẳng y là hai đường thẳng …

b) Đường thẳng a và đường thẳng b là hai đường thẳng …

c) Đường thẳng x và đường thẳng a là hai đường thẳng …

d) Đường thẳng a và đường thẳng MO là hai đường thẳng …

Hướng dẫn giải:

 a) Vì hai đường thẳng x và y không có điểm chung nên đường thẳng x và đường thẳng y là hai đường thẳng song song.

b) Vì hai đường thẳng a và b có một điểm chung là điểm M nên đường thẳng a và đường thẳng b là hai đường thẳng cắt nhau.

c) Vì hai đường thẳng x và a có một điểm chung là điểm M nên đường thẳng x và đường thẳng a là hai đường thẳng cắt nhau.

d) Đường thẳng a và đường thẳng MO nằm “chồng khít” lên nhau nên đường thẳng a và đường thẳng MO là hai đường thẳng trùng nhau.

3. Điểm nằm giữa hai điểm

Phương pháp giải

Nếu điểm B nằm giữa hai điểm A và C thì ta có:

- Hai điểm A và C nằm khác phía đối với điểm B.

- Hai điểm A và B nằm cùng phía đối với điểm C.

- Hai điểm B và C nằm cùng phía đối với điểm  A.

Ví dụ. Vẽ bốn điểm A, B, C, D sao cho điểm A nằm giữa hai điểm B và C, điểm D nằm giữa hai điểm A và C.

a) Điểm A nằm giữa hai điểm nào?

b) Tìm các điểm nằm khác phía đối với điểm D.

Hướng dẫn giải:

 Vì điểm A nằm giữa hai điểm B và C, điểm D nằm giữa hai điểm A và C nên điểm A và điểm D nằm giữa hai điểm B và C, điểm A nằm giữa hai điểm B và D.

a) Điểm A nằm giữa hai điểm: B và D; B và C;

b) Các điểm nằm khác phía đối với điểm D là: B và C; A và C.

4. Nhận biết tia, hai tia đối nhau

Phương pháp giải

* Nhận biết tia

- Xem xét định nghĩa của tia là gốc và phần đường thẳng bị chia ra bởi gốc.

- Khi đọc (viết) tên một tia, phải đọc (viết) tên gốc trước.

Chẳng hạn: Tia Ox gồm điểm gốc O và phần đường thẳng bị chia bởi gốc O.

* Nhận biết hai tia đối nhau

- Xét xem hai tia đối nhau thì có chung gốc và tạo thành một đường thẳng.

Chẳng hạn: Tia Ox và tia Oy là hai tia đối nhau.

Lưu ý: Mỗi điểm nằm trên đường thẳng là gốc của hai tia đối nhau.

- Nếu tia OA và tia OB đối nhau thì điểm O nằm giữa hai điểm A và B.

Ví dụ. Cho hai tia AM và AN là hai tia đối nhau, điểm I nằm trên tia AN. Trong ba điểm A, M, I, điểm nào nằm giữa hai điểm còn lại?

Hướng dẫn giải:

Vì hai tia AM và AN là hai tia đối nhau nân điểm A nằm giữa hai điểm M và N.

Vì điểm I nằm trên tia AN nên điểm A nằm giữa hai điểm M và I.

5. Nhận biết đoạn thẳng, đo độ dài đoạn thẳng

Phương pháp giải

Đoạn thẳng gồm hai đầu mút và tất cả các điểm nằm giữa hai đầu mút (mút).

Chẳng hạn: Đoạn thẳng AB hay đoạn thẳng BA có hai đầu mút là A và B.

- Với n điểm phân biệt cho trước ($\text{n}\in \mathbb{N},\text{ n}\ge \text{2}$) thì số đoạn thẳng vẽ được là: $\frac{n.(n-1)}{2}$.

- Đo độ dài đoạn thẳng AB bằng cách dùng thước đo độ dài đo khoảng cách từ điểm A đến điểm B.

- Nếu hai điểm trùng nhau thì khoảng cách giữa chúng bằng 0.

- Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB.

Ngược lại, nếu AM + MB = AB thì điểm M nằm giữa hai điểm A và B.

Ví dụ. Cho ba điểm A, B, C nằm trên đường thẳng x, điểm B nằm giữa hai điểm A và C. Biết độ dài các đoạn thẳng: AB = 2 cm, BC = 3 cm. Tính độ dài đoạn thẳng AC.

Hướng dẫn giải:

Vì điểm B nằm giữa hai điểm A và C nên ta có: AB + BC = AC.

Thay AB = 2 cm, BC = 3 cm, ta được: AC = 2 + 3 = 5 (cm).

Vậy AC = 5 cm.

6. So sánh độ dài đoạn thẳng

Phương pháp giải

•Hai đoạn thẳng AB và CD bằng nhau hay có cùng độ dài, kí hiệu là AB = CD.

Ví dụ.

Vì 3 cm < 4 cm nên AB < CD. Do đó, đoạn thẳng AB ngắn hơn (nhỏ hơn) đoạn thẳng CD.

•Đoạn thẳng AB dài hơn (lớn hơn) đoạn thẳng CD, kí hiệu là AB > CD.

7. Nhận biết trung điểm của đoạn thẳng

Phương pháp giải

Ta sử dụng định nghĩa trung điểm của đoạn thẳng để nhận biết trung điểm của đoạn thẳng như sau:

Giả sử cho 3 điểm A , B và C. Để chứng minh B là trung điểm của AC, ta có:

Bước 1: Chứng minh điểm B nằm giữa 2 điểm A và C hay B thuộc đoạn thẳng AC.

Bước 2: Chứng minh độ dài hai đoạn thẳng AB và BC bằng nhau hay AB = BC và AB + BC = AC.

Bước 3: Kết luận B là trung điểm của AC dựa trên 2 đặc điểm: nằm giữa và tạo thành 2 đoạn thẳng bằng nhau.

Ví dụ. Trên đường thẳng xy cho ba điểm A, B, C theo thứ tự. Gọi M và N lần lượt là trung điểm của AB và BC. Chứng minh rằng: $MN=\frac{AC}{2}$

Hướng dẫn giải:

M là trung điểm của AB: $MN=\frac{AB}{2}$

N là trung điểm của BC: $NC=\frac{BC}{2}$

Khi đó: $MN=MB+BN=\frac{AB}{2}+\frac{BC}{2}=\frac{AB+BC}{2}=\frac{AC}{2}$

8. Tính độ dài đoạn thẳng

Phương pháp giải

Để tính độ dài của một đoạn thẳng ta thường làm như sau:

– Bước 1: Chỉ ra một điểm nằm giữa hai điểm còn lại.

– Bước 2: Sử dụng nhận xét “Nếu điểm M nằm giữa hai điểm A và B thì AM + MB = AB”.

Chú ý: Để chứng minh ba điểm A, B, C thẳng hàng ta cần chứng minh một điểm nằm giữa hai điểm còn lại.

Ví dụ. Cho đoạn thẳng AB = 10 cm. Điểm M nằm giữa hai điểm A và B sao cho
AM =  MB + 2. Tính độ dài các đoạn thẳng AM; MB.

Hướng dẫn giải:

Vì M nằm giữa hai điểm A và B nên AM + MB = AB hay AM + MB = 10 (1)

Mà AM = MB + 2 (2)

Thay (2) vào (1) ta có: MB + 2 + MB = 10 suy ra 2MB + 2 = 10

Suy ra $MB=\frac{10-2}{2}=4\left(cm\right)$

Có AM = MB + 2 = 4 + 2 = 6 (cm)

9. Nhận biết góc, đỉnh và cạnh của góc. Góc bẹt

Phương pháp giải

- Trong hình vẽ có góc xOy (hoặc góc yOx) được kí hiệu là $\widehat{xOy}$ gồm đỉnh O, hai tia Ox và cạnh Oy được gọi là cạnh của góc.

- Khi Ox và Oy là hai tia đối nhau, ta có góc bẹt xOy.

Ví dụ. Vẽ hình theo hướng dẫn sau:

- Vẽ đường thẳng xy.

- Lấy điểm A thuộc đường thẳng xy.

- Lấy điểm B không thuộc đường thẳng xy.

- Vẽ tia BA.

Kể tên các góc có trong hình vừa vẽ và chỉ ra góc bẹt có trong các góc đó.

Hướng dẫn giải:

Ta có hình vẽ:

- Các góc có trong hình vẽ là: $\widehat{xAB};\widehat{BAx};\widehat{xAy}$.

- Vì Ax và Ay là hai tia đối nhau nên $\widehat{xAy}$ là góc bẹt.

10. Điểm trong một góc

Phương pháp giải

Khi hai tia Ox và Oy không đối nhau, điểm M gọi là điểm nằm trong góc xOy nếu tia OM nằm giữa hai tia Ox và Oy. Khi đó tia OM nằm trong góc xOy.

Nếu tia OM nằm trong góc xOy thì mọi điểm thuộc tia OM đều nằm trong góc xOy.

Ví dụ. Cho góc xOy khác góc bẹt, tia Oz nằm trong góc đó, tia Ot nằm trong góc xOz. Chứng minh tia Ot nằm trong góc xOy.

Hướng dẫn giải:

Ta có hình vẽ:

Lấy A thuộc Ox, lấy B thuộc Oy, AB cắt Oz tại C.

Suy ra C nằm giữa 2 điểm A và B vì Oz nằm trong góc xOy.

Vì tia Ot nằm trong góc xOz nên đoạn thẳng AC cắt tia Ot ở D, D nằm giữa 2 điểm A và C.

Vì C nằm giữa A và B, D nằm giữa A và C nên điểm D nằm giữa A và B. Do vậy Ot nằm trong góc xOy.

11. Nhận biết khái niệm số đo góc và nắm được cách đo góc

Phương pháp giải

*Ta nhận biết số đo góc dựa vào khái niệm:

+ Mỗi góc có một số đo. Số đo của góc bẹt là 180º.

+ Số đo của mỗi góc không vượt quá 180º.

+ Khi hai tia Ox, Oy trùng nhau, trong trường hợp cần thiết ta cũng coi góc xOy là một góc và gọi là “góc không”, số đo của góc không là 0°.

* Cách đo góc:

+ Dụng cụ: Thước đo góc

+ Cách làm:

Bước 1: Ta đặt thước đo góc sao cho tâm của thước trùng với đỉnh O của góc.

Bước 2: Xoay thước sao cho một cạnh của góc (chẳng hạn, cạnh Oy) đi qua vạch 0 của thước và thước chồng lên phần trong của góc như trên.

Bước 3: Xác định xem cạnh còn lại của góc (cạnh Ox) đi qua vạch chỉ số nào trên thước đo góc, ta sẽ được số đo của góc đó.

Ví dụ. Tìm số đo của góc của kim giờ và kim phút lúc 2 giờ, 5 giờ, 6 giờ, 10 giờ.

Hướng dẫn giải:

Lúc 6 giờ, kim giờ chỉ số 6 và kim phút chỉ số 12. Khi đó hai kim thẳng hàng và chúng tạo thành góc bẹt 180°. Mỗi giờ kim giờ quay được một góc 180° : 6 = 30°.

Góc giữa hai kim:

•Lúc 2 giờ là 30° . 2 = 60°.

•Lúc 3 giờ là 30° . 3 = 90°.

•Lúc 5 giờ là 30° . 5 = 150°.

•Lúc 6 giờ là 30° . 6 = 180°.

12. Các góc đặc biệt (góc vuông, góc nhọn, góc tù)

Phương pháp giải

Ta dựa vào định nghĩa để nhận biết các góc đặc biệt như sau:

+ Góc nhọn là góc có số đo lớn hơn 0° và nhỏ hơn 90°.

+ Góc vuông là góc có số đo bằng 90°.

+ Góc tù là góc có số đo lớn hơn 90° và nhỏ hơn 180°.

Ví dụ. Trong các hình dưới đây, có bao nhiêu hình có góc vuông, bao nhiêu hình có góc nhọn và bao nhiêu hình có góc tù?

Hướng dẫn giải:

Góc vuông: 2 hình (Hình 2, Hình 5).

Góc nhọn: 3 hình (Hình 1, Hình 3, Hình 4).

Góc tù: 1 hình (Hình 3).