Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Xác suất thực nghiệm được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Xác suất thực nghiệm. Mời các bạn đón xem:
Bài tập Toán 6 Xác suất thực nghiệm
A. Bài tập Xác suất thực nghiệm
Bài 1. Dũng tung một con xúc xắc 10 lần thấy có 2 lần ra mặt 6 chấm.
Hãy tính xác suất thực nghiệm của sự kiện “Mặt xuất hiện là mặt 6 chấm”.
Hướng dẫn giải:
Xác suất thực nghiệm xuất hiện mặt 6 chấm là:
Vậy xác suất thực nghiệm xuất hiện mặt 6 chấm là
Bài 2. Một chiếc thùng kín có một số quả bóng màu xanh, đỏ, tím, vàng có cùng kích thước. Trong một trò chơi, người chơi lấy ngẫu nhiên một quả bóng, ghi lại màu rồi trả lại bóng vào thùng. Bình thực hiện trò chơi 100 lần và được kết quả như bảng sau:
|
Màu |
Số lần |
|
Xanh |
43 |
|
Đỏ |
22 |
|
Tím |
18 |
|
Vàng |
17 |
Tính xác suất thực nghiệm của các sự kiện sau:
a) Bình lấy được quả bóng màu xanh;
b) Quả bóng được lấy ra không là màu đỏ.
Hướng dẫn giải
a) Xác suất thực nghiệm của các sự kiện Bình lấy được quả bóng màu xanh là:
b) Để lấy ra được quả bóng không là màu đỏ nghĩa là lấy được các màu còn lại xanh, tím và vàng
Số lần lấy được quả bóng không phải là màu đỏ là: 100 – 22 = 78 (lần)
Xác suất thực nghiệm của các sự kiện quả bóng được lấy ra không là màu đỏ là:
Vậy xác suất thực nghiệm của các sự kiện Bình lấy được quả bóng màu xanh; Quả bóng được lấy ra không là màu đỏ lần lượt là 0,43 và 0,78.
Bài 3.
a) Nếu gieo một xúc xắc 11 lần liên tiếp, có 5 lần xuất hiện mặt 2 chấm thì xác suất thực nghiệm xuất hiện mặt 2 chấm bằng bao nhiêu?
b) Nếu gieo một xúc xắc 14 lần liên tiếp, có 3 lần xuất hiện mặt 6 chấm thì xác suất thực nghiệm xuất hiện mặt 6 chấm bằng bao nhiêu?
Hướng dẫn giải
a) Xác suất thực nghiệm xuất hiện mặt 2 chấm là:
b) Xác suất thực nghiệm xuất hiện mặt 6 chấm là:
Bài 4. Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
8 |
6 |
10 |
9 |
8 |
9 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Gieo được mặt có 5 chấm.
b) Gieo được mặt có số chẵn chấm.
Lời giải:
a) Số lần xuất hiện mặt 5 chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 8.
Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có 5 chấm” là: 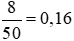 .
.
b) Số mặt có chẵn chấm là các mặt có 2 chấm, 4 chấm và 6 chấm.
Số lần xuất hiện mặt 2 chấm là: 6.
Số lần xuất hiện mặt 4 chấm là: 9.
Số lần xuất hiện mặt 6 chấm là: 9.
Do đó, số lần xuất hiện mặt có chẵn chấm của con xúc xắc 6 mặt trong 50 lần gieo là: 6 + 9 + 9 = 24.
Vậy xác suất thực nghiệm của sự kiện “Gieo được mặt có số chẵn chấm” là: 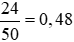
Bài 5. Trong hộp có một số viên bi màu xanh, đỏ và vàng có kích thước giống nhau. Lấy ngẫu nhiên một viên bi từ hộp, xem màu rồi trả lại lại. Lặp lại hoạt động đó 80 lần ta được kết quả như sau:
|
Loại bi |
Bi xanh |
Bi đỏ |
Bi vàng |
|
Số lần |
22 |
45 |
13 |
a) Tính xác suất thực hiện của sự kiện “lấy được viên bi xanh”.
b) Em hãy dự đoán xem trong hộp loại bi nào có nhiều hơn.
Lời giải:
a) Số lần lấy được bi xanh trong 80 lần lấy bi từ hộp là 22.
Vậy xác suất thực nghiệm của sự kiện “lấy được viên bi xanh” trong 80 lần lấy là: 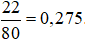
b) Tổng số viên bi xanh và viên bi vàng là: 22 + 13 = 35 (viên bi)
Ta thấy: số lần lấy được viên bi đỏ nhiều hơn so với số lần lấy được viên bi xanh và viên bi vàng.
Vậy có thể dự đoán là trong hộp đó số viên bi đỏ nhiều hơn số viên bi đỏ và số viên bi vàng.
Bài 6. Số điện thoại một cửa hàng bán được trong 30 ngày của tháng 8 được cho ở bảng sau:
|
5 |
7 |
4 |
5 |
5 |
3 |
5 |
3 |
6 |
7 |
|
4 |
7 |
8 |
5 |
2 |
7 |
3 |
6 |
4 |
12 |
|
5 |
8 |
6 |
4 |
9 |
5 |
8 |
9 |
5 |
5 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Cửa hàng bán được 5 chiếc điện thoại một ngày.
b) Cửa hàng bán được trên 7 chiếc điện thoại một ngày.
Lời giải:
a) Số ngày cửa hàng bán được 5 chiếc điện thoại trong 30 ngày là 9.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được 5 chiếc điện thoại một ngày” là: 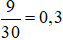 .
.
b) Số ngày cửa hàng bán được trên 7 chiếc điện thoại bằng tổng số các ngày cửa hàng bán được 8 chiếc điện thoại, 9 chiếc điện thoại và 12 chiếc điện thoại.
Số ngày cửa hàng bán được 8 chiếc điện thoại là: 3.
Số ngày cửa hàng bán được 9 chiếc điện thoại là: 2.
Số ngày cửa hàng bán được 12 chiếc điện thoại là: 1.
Số ngày cửa hàng bán được trên 7 chiếc điện thoại một ngày trong 30 ngày là:
3 + 2 + 1 = 6.
Vậy xác suất thực nghiệm của sự kiện “Cửa hàng bán được trên 7 chiếc điện thoại một ngày” là: 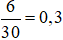
Bài 7. Trong hộp có một số bút màu xanh và một số bút màu đỏ, lấy ngẫu nhiên 1 bút từ hộp, xem màu rồi trả lại. Lặp lại hoạt động trên 50 lần, ta được kết quả theo bảng sau:
|
Loại bút |
Bút màu xanh |
Bút màu đỏ |
|
Số lần |
42 |
8 |
a) Hãy tìm xác suất của thực nghiệm xuất hiện màu xanh khi lấy bút.
b) Em hãy dự đoán xem trong hộp loại bút nào nhiều hơn.
Hướng dẫn giải
a) Quan sát bảng ta thấy số lần xuất hiện bút màu xanh là 42 lần.
Xác suất của thực nghiệm xuất hiện màu xanh khi lấy bút là: .
b) Để dự đoán xem trong hộp loại bút nào nhiều hơn ta tính thêm xác suất của thực nghiệm xuất hiện màu xanh khi lấy bút.
Quan sát bảng ta thấy số lần xuất hiện bút màu đỏ là 8 lần.
Xác suất của thực nghiệm xuất hiện màu đỏ khi lấy bút là: .
Ta thấy 0,84 > 0,16 nên xác suất của thực nghiệm lấy được bút màu xanh lớn hơn bút đỏ, do đó ta có thể dự đoán rằng trong hộp bút xanh có nhiều hơn.
Bài 8. Gieo con súc sắc có 6 mặt 100 lần, kết quả thu được ghi ở bảng sau
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần xuất hiện |
17 |
18 |
15 |
14 |
16 |
20 |
a) Hãy tìm xác suất của thực nghiệm xuất hiện mặt 6 chấm.
b) Hãy tìm xác suất của thực nghiệm xuất hiện mặt chấm chẵn.
c) Hãy tìm xác suất của thực nghiệm xuất hiện mặt chấm lẻ.
Hướng dẫn giải
a) Quan sát bảng ta thấy số lần xuất hiện mặt 6 chấm là 20 lần.
Xác suất của thực nghiệm xuất hiện mặt 6 chấm là: .
b) Các mặt chấm chẵn của xúc xắc là mặt 2, 4, 6.
Tổng số lần xuất hiện mặt chấm chẵn là: 18 + 14 + 20 = 52 (lần).
Xác suất của thực nghiệm xuất hiện mặt chấm chẵn là:
c) Các mặt chấm lẻ của xúc xắc là mặt 1, 3, 5.
Tổng số lần xuất hiện mặt chấm lẻ là: 17 + 15 + 15 = 48 (lần).
Xác suất của thực nghiệm xuất hiện mặt chấm lẻ là:
Câu 9: Hằng ngày Sơn đều đi xe buýt đến trường. Sơn ghi lại thời gian chờ xe của mình trong 20 lần liên tiếp ở bảng sau:
Hãy tính xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút”
A.0,1
B.0,2
C.0,9
D.0,5
Trả lời:
Tổng số lần Sơn chờ xe là 20 lần.
Số lần Sơn phải chờ xe dưới 2 phút là 5 lần.
Số lần Sơn phải chờ xe từ 2 phút đến dưới 5 phút là 9 lần.
Số lần Sơn phải chờ xe từ 5 phút đến dưới 10 phút là 4 lần.
Số lần Sơn phải chờ xe dưới 10 phút là 5 + 9 + 4 = 18 lần.
Xác suất thực nghiệm của sự kiện “Sơn phải chờ xe dưới 10 phút” là:
Đáp án cần chọn là: C
Câu 10: Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
|
Màu bút |
Bút xanh |
Bút vàng |
Bút đỏ |
|
Số lần |
14 |
10 |
16 |
Tính xác suất thực nghiệm của sự kiện lấy được màu đỏ
A.0,16
B.0,6
C.0,4
D.0,45
Trả lời:
Tổng số lần lấy là 40.
Số lần lấy được màu đỏ là 16.
Xác suất thực nghiệm của sự kiện lấy được màu đỏ là:
Đáp án cần chọn là: C
Câu 11: Trong hộp có một số bút xanh, một số bút vàng và một số bút đỏ. lấy ngẫu nhiên 1 bút từ hộp, xem màu gì rồi trả lại. Lặp lại hoạt động trên 40 lần ta được kết quả như sau:
|
Màu bút |
Bút xanh |
Bút vàng |
Bút đỏ |
|
Số lần |
14 |
10 |
16 |
Tính xác suất thực nghiệm của sự kiện không lấy được màu vàng
A.0,25
B.0,75
C.0,1
D.0,9
Trả lời:
Tổng số lần lấy bút là 40.
Số lần lấy được màu vàng là 10
Số lần không lấy được màu vàng là 40 – 10 = 30.
Xác suất suất thực nghiệm của sự kiện không lấy được màu vàng là:
Đáp án cần chọn là: B
Câu 12. Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Môn Toán đạt loại giỏi
A.
B.
C.
D.
Trả lời:
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Số học sinh được loại giỏi môn Toán là 40 + 20 + 15 = 75
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại giỏi môn Toán là
Đáp án cần chọn là: A
Câu 13. Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Loại khá trở lên ở cả hai môn
A.
B.
C.
D.
Trả lời:
Tổng số học sinh là tổng tất cả các số trên bảng: 170.
Các học sinh được loại khá trở lên ở cả 2 môn:
+ Toán giỏi, Ngữ văn giỏi: 40
+ Toán giỏi, Ngữ văn khá: 20
+ Toán khá, Ngữ văn giỏi: 15
+ Toán khá, Ngữ văn khá: 30
Số học sinh được loại khá trở lên ở cả 2 môn là:
40+20+15+30=105
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên được loại khá trở lên ở cả 2 môn là:
Đáp án cần chọn là: C
Câu 14. Kết quả kiểm tra môn Toán và Ngữ văn của một số học sinh được lựa chọn ngẫu nhiên cho ở bảng sau:
Ví dụ: Số học sinh có kết quả Toán – giỏi, Ngữ văn – giỏi là 40. Minh họa
Hãy tính xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả:
Loại trung bình ở ít nhất một môn
A.
B.
C.
D.
Trả lời:
Tổng số học sinh là 170.
Các học sinh được loại trung bình ở ít nhất một môn là:
+ Toán trung bình, Văn giỏi: 5
+ Toán trung bình, Văn khá: 15
+ Toán trung bình, Văn trung bình: 20
+ Văn trung bình, Toán giỏi: 15
+ Văn trung bình, Toán khá: 10
Số học sinh được loại trung bình ở ít nhất một môn là:
5 + 15 + 20 + 15 + 10 = 65
Xác suất thực nghiệm của sự kiện một học sinh được chọn ra một cách ngẫu nhiên có kết quả được loại trung bình ít nhất một môn:
Đáp án cần chọn là: B
Câu 15. Nếu tung một đồng xu 22 lần liên tiếp thì, có 14 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt N bằng bao nhiêu?
A.
B.
C.
D.
Trả lời:
Tổng số lần gieo là 22.
Số lần gieo được mặt N là 14.
Xác suất thực nghiệm xuất hiện mặt N là:
Đáp án cần chọn là: A
Câu 16. Nếu tung một đồng xu 30 lần liên tiếp có 12 lần xuất hiện mặt N thì xác suất thực nghiệm xuất hiện mặt S bằng bao nhiêu?
A.
B.
C.
D.
Trả lời:
Tổng số lần gieo là 30.
Số lần gieo được mặt S là 30 – 12 = 18.
Xác suất thực nghiệm xuất hiện mặt S là:
Đáp án cần chọn là: C
Câu 17. Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 1
A. 0,4
B. 0,14
C. 0,16
D. 0, 25
Trả lời:
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 1 là 4 lần.
Xác suất thực nghiệm xuất hiện số 1 là
Đáp án cần chọn là: C
Câu 18. Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số 2
A. 0,42
B. 0,24
C. 0,12
D. 0,6
Trả lời:
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Xác suất thực nghiệm xuất hiện số 2 là
Đáp án cần chọn là: B
Câu 19. Một hộp có 5 chiếc thẻ cùng loại, mỗi thẻ được ghi một trong các số 1, 2, 3, 4, 5; hai thẻ khác nhau thì ghi số khác nhau. Rút ngẫu nhiên một thẻ rồi bỏ lại thẻ vào hộp.
Sau 25 lần rút thẻ liên tiếp, hãy ghi kết quả thống kê theo mẫu sau:
|
Lần 1 |
Số 3 |
Lần 6 |
Số 5 |
Lần 11 |
Số 3 |
Lần 16 |
Số 2 |
Lần 21 |
Số 1 |
|
Lần 2 |
Số 1 |
Lần 7 |
Số 2 |
Lần 12 |
Số 2 |
Lần 17 |
Số 1 |
Lần 22 |
Số 5 |
|
Lần 3 |
Số 2 |
Lần 8 |
Số 3 |
Lần 13 |
Số 2 |
Lần 18 |
Số 2 |
Lần 23 |
Số 3 |
|
Lần 4 |
Số 3 |
Lần 9 |
Số 4 |
Lần 14 |
Số 1 |
Lần 19 |
Số 3 |
Lần 24 |
Số 4 |
|
Lần 5 |
Số 4 |
Lần 10 |
Số 5 |
Lần 15 |
Số 5 |
Lần 20 |
Số 5 |
Lần 25 |
Số 5 |
Tính xác suất thực nghiệm
Xuất hiện số chẵn
A. 0,24
B. 0,63
C. 0,36
D. 0,9
Trả lời:
Tổng số lần rút là 25 lần.
Số lần xuất hiện số 2 là 6 lần.
Số lần xuất hiện số 4 là 3 lần.
Số lần xuất hiện số chẵn là 6 + 3 = 9 lần.
Xác suất thực nghiệm xuất hiện số 2 là
Đáp án cần chọn là: C
Câu 20: Gieo một con xúc xắc 6 mặt 50 lần ta được kết quả như sau:
|
Mặt |
1 chấm |
2 chấm |
3 chấm |
4 chấm |
5 chấm |
6 chấm |
|
Số lần |
8 |
7 |
3 |
12 |
10 |
10 |
Hãy tính xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần gieo trên.
A.0,21
B.0,44
C.0,42
D.0,18
Trả lời:
Tổng số lần gieo là 50.
Các mặt có số lẻ chấm của con xúc xắc là mặt 1, 3 và 5.
Số lần được mặt 1 chấm là 8 lần, mặt 3 chấm là 3 lần, mặt 5 chấm là 10 lần.
Số lần được mặt có số lẻ chấm là 8 + 3 + 10 = 21 lần
Xác suất thực nghiệm của sự kiện gieo được mặt có số lẻ chấm trong 50 lần là:
Đáp án cần chọn là: C
B. Lý thuyết Xác suất thực nghiệm
1. Khả năng xảy ra của một sự kiện
Khi thực hiện một phép thử nghiệm, một sự kiện có thể xảy ra hoặc không thể xảy ra. Để nói về khả năng xảy ra của mỗi sự kiện, ta dùng một con số có giá trị từ 0 đến 1.
Một sự kiện không thể xảy ra có khả năng xảy ra bằng 0.
Một sự kiện chắc chắn xảy ra có khả năng xảy ra bằng 1.
Ví dụ 1. Trong hộp có 3 quả bóng: bóng xanh, bóng đỏ và bóng vàng. Không nhìn vào hộp, chọn ra từ hộp một quả bóng. Xét khả năng xảy ra của mỗi sự kiện sau:
a) Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng;
b) Bóng chọn ra có màu tím.
Lời giải:
a) Khi chọn một quả bóng từ hộp thì quả bóng được chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng.
Do đó, sự kiện này chắc chắn xảy ra.
Vậy sự kiện “Bóng chọn ra có một trong ba quả: bóng xanh, bóng đỏ hoặc bóng vàng” có khả năng xảy ra bằng 1.
b) Vì ba quả trong hộp không có quả bóng nào có màu tím nên sự kiện “Bóng chọn ra có màu tím” không xảy ra.
Vậy sự kiện “Bóng chọn ra có màu tím” có khả năng xảy ra bằng 0.
2. Xác suất thực nghiệm
Thực hiện lặp đi lặp lại một hoạt động nào đó n lần. Gọi n(A) là số lần sự kiện A xảy ra trong n lần đó. Tỉ số
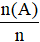 = Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
= Số lần sự kiện A xảy ra : Tổng số lần thực hiện hoạt động
được gọi là xác suất thực nghiệm của sự kiện A sau n hoạt động vừa thực hiện.
Ví dụ 2. Tung hai đồng xu cân đối 40 lần ta được kết quả như sau:
|
Sự kiện |
Hai đồng sấp |
Một đồng sấp, một đồng ngửa |
Hai đồng ngửa |
|
Số lần |
12 |
15 |
13 |
Hãy tính xác suất thực nghiệm của sự kiện:
a) Hai đồng xu sấp.
b) Có một đồng xu sấp, một đồng xu ngửa.
Lời giải:
a) Xác suất thực nghiệm của sự kiện “Hai đồng xu sấp” tung 40 lần tung là:
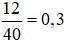
b) Xác suất thực nghiệm của sự kiện “Có một đồng xu sấp, một đồng xu ngửa” tung 30 lần tung là: