Bài 1. Phân tích các số sau ra thừa số nguyên tố: 60; 121; 225.

Lời giải

Ta sẽ sử dụng sơ đồ cột

Vậy 60 = 2².3.5

Vậy 121 = 11²

Vậy 225 = 3².5²

Bài 2. Các khẳng định sau đúng hay sai? Vì sao?

a) Ước nguyên tố của 12 là 1; 2; 3.

b) Tích hai số nguyên tố bất kì luôn là số chẵn.

c) Mọi số chẵn đều là hợp số.

d) Mọi số lẻ đều là số nguyên tố.

Lời giải

a) 1; 2; 3 là các ước của 12, trong đó 2 và 3 là số nguyên tố còn 1 không phải là số nguyên tố nên a sai.

b) Ta có 3 và 5 là hai số nguyên tố. Tích 3.5 = 15 không phải là số chẵn. Do đó b sai.

c) Số 2 là số chẵn nhưng 2 là số nguyên tố nên c sai.

d) Ta có 15 là số lẻ nhưng 15 không phải là số nguyên tố. Do đó d sai.

Bài 3: Mỗi số sau là số nguyên tố hay hợp số? Giải thích.

a) 19;

b) 125;

c) 187;

d) 59.

Hướng dẫn giải

a) Vì 19 chỉ có đúng hai ước là 1 và chính nó nên 19 là số nguyên tố.

b) Vì 125 có ước là 5 khác 1 và chính nó nên 125 có nhiều hơn 2 ước. Do đó 125 là hợp số.

c) Vì 187 có ước là 11 khác 1 và chính nó nên 187 có nhiều hơn 2 ước. Do đó 187 là hợp số.

d) Vì 59 chỉ có đúng hai ước là 1 và chính nó nên 59 là số nguyên tố.

Bài 4: Phân tích mỗi số sau ra thừa số nguyên tố rồi cho biết mỗi số chia hết cho các số nguyên tố nào?

a) 40;

b) 144;

c) 300.

Hướng dẫn giải

a) Ta có:

Do đó 40 = 2³ . 5.

Số 40 có thể chia hết cho các số nguyên tố là 2 và 5.

b) Ta có:

Do đó 144 = 2⁴ . 3².

Số 144 có thể chia hết cho các số nguyên tố là 2 và 3.

c) Ta có:

Do đó 300 = 2² . 3 . 5².

Số 300 có thể chia hết cho các số nguyên tố là 2; 3 và 5.

Bài 5: Các số tự nhiên từ 1991 đến 2005 thì số nào là số nguyên tố?

Hướng dẫn giải

Các số tự nhiên từ 1991 đến 2005 là số nguyên tố:

− Ta loại bỏ các số chẵn: 1992; 1994; 1996; …; 2004.

− Loại bỏ tiếp các số chia hết cho 3: 1995; 2001.

− Ta còn phải xét các số 1991; 1993; 1997; 1999; 2003. Ta tìm số nguyên tố p mà p² < 2005 là 11, 13, 17, 19, 23, 29, 31, 37, 41, 43.

− Số 1991 chia hết cho 11 nên ta loại.

− Các số còn lại 1993, 1997, 1999, 2003 đều không chia hết cho các số nguyên tố trên.

Vậy từ 1991 đến 2005 chỉ có 4 số nguyên tố là 1993, 1997, 1999, 2003.

Bài 6. Chứng minh rằng mọi số nguyên tố lớn hơn 2 đều có dạng là 4n ± 1 với n là số tự nhiên bất kì. 

Lời giải:

Khi chia một số tự nhiên a lớn hơn 2 cho 4 thì ta được các số dư là 0, 1, 2, 3. Trường hợp các số dư là 0 và 2 thì a là hợp số. 

Thật vậy,

+ Với số dư là 0 thì a chia hết cho 4 nên a là hợp số

+ Với số dư là 2, ta có: a = 4n + 2 

Vì 4 chia hết cho 2 nên 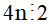 , 2 chia hết cho 2

Do đó: 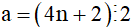nên a là hợp số

Ta xét trường hợp số dư là 1 và 3.

+ Với mọi trường hợp số dư là 1 ta có a = 4n + 1

+ Với mọi trường hợp số dư là 3 ta có a = 4n + 3 = 4n + 4 – 1 = 4(n + 1) – 1 

Đặt n + 1 = m, khi đó a = 4m – 1

Từ đó suy ra điều phải chứng minh. 

Câu 7. Phân tích một số ra thừa số nguyên tố là:

A. phân tích số đó thành tích của số nguyên tố với các hợp số.

B. phân tích số đó thành tích của các số tự nhiên.

C. Phân tích số đó thành tích của các thừa số nguyên tố.

D. Phân tích số đó thành tích của hai thừa số nguyên tố.

Lời giải Phân tích một số ra thừa số nguyên tố là phân tích số đó thành tích của các thừa số nguyên tố.

Đáp án: D

Câu 8. Có bao nhiêu cách để phân tích một số ra thừa số nguyên tố?

A. 1;

B. 2;

C. 3;

D. 4.

Lời giải

Có hai cách phân tích một số ra thừa số nguyên tố là: 

+ Phương pháp phân tích theo sơ đồ cây;

+ Phương pháp phân tích theo sơ đồ cột.

Đáp án: B

Câu 9. Có bao nhiêu khẳng định đúng trong các khẳng định sau?

a) Ước nguyên tố của 18 là 1; 2; và 3.

b) Tích của hai số nguyên tố bất kì luôn là số lẻ.

c) Mọi số chẵn đều là hợp số.

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải

Ước nguyên tố của 18 chỉ có 2 và 3, 1 không phải số nguyên tố nên a sai.

2 là số nguyên tố, 3 là số nguyên tố. Ta có tích 2.3 = 6 là số chẵn nên b sai.

Ta có 2 là số chẵn, 2 cũng là số nguyên tố nên c sai.

Vậy không có phát biểu nào đúng.

Đáp án: A

Câu 10. Tìm chữ số a để $\overline{49a}$là số nguyên tố:

A. 1;

B. 9;

C. A và B đều đúng;

D. cả A và B đều sai.

Lời giải

Dựa vào bảng số nguyên tố ở cuối sách giáo khoa ta có:

491 và 499 là hai số nguyên tố nên a = 1 hoặc a = 9. 

Đáp án: C

Câu 11. Số nào trong các số sau là số nguyên tố?

A. 3;

B. 8;

C. 12;

D. 15.

Lời giải

Trong các số đã cho:

3 có hai ước là 1 và 3. Do đó 3 là số nguyên tố.

8 có 4 ước là 1; 2; 4; và 8 nên 8 là hợp số.

12 có 6 ước là 1; 2; 3; 4; 6 và 12 nên 12 là hợp số.

15 có 4 ước là 1; 3; 5 và 15 nên 15 là hợp số.

Đáp án: A

Câu 12. Trong các số sau: 16; 17; 20; 21; 23; 97. Có bao nhiêu số là hợp số?

A. 0;

B. 1;

C. 2;

D. 3.

Lời giải

16 có 5 ước là 1; 2; 4; 8; 16 nên 16 là hợp số.

17 có 2 ước là 1 và 17 nên 17 là số nguyên tố.

20 có 6 ước là 1; 2; 4; 5; 10 và 20 nên 20 là hợp số.

21 có 4 ước là 1; 3; 7 và 21 nên 21 là hợp số.

23 có 2 ước là 1 và 23 nên 23 là số nguyên tố.

97 có 2 ước là 1 và 97 nên 97 là số nguyên tố.

Vậy có 3 số là hợp số. 

Đáp án: D

Câu 13. Hoàn thành phát biểu sau: “Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có …”:

A. ước là 1.

B. ước là chính nó.

C. duy nhất một ước.

D. hai ước là 1 và chính nó.

Lời giải Số nguyên tố là số tự nhiên lớn hơn 1, chỉ có hai ước là 1 và chính nó.

Đáp án: D

Câu 14. Cho A là tập hợp các số nguyên tố nhỏ hơn 30. Chọn đáp án đúng.

A. 1 ∈ A;

B. 2 ∉ A;

C. 29 ∉ A;

D. 17 ∈ A

Lời giải

Các số nguyên tố nhỏ hơn 30 bao gồm: 2; 3; 5; 7; 11; 13; 17; 23; 29.

Do đó A = {2; 3; 5; 7; 11; 13; 17; 23; 29}.

Ta có 1 không thuộc tập A, ta viết 1 ∉ A nên A sai.

Ta có 2 thuộc tập A, ta viết 2 ∈ A nên B sai.

Ta có 29 thuộc tập A, ta viết 29 ∈ A nên C sai.

Ta có 17 thuộc tập A, ta viết 17 ∈ A nên D đúng.

Đáp án: D

Câu 15. Hãy phân tích A = 4².9⁵ ra thừa số nguyên tố.

A. A = 4².9⁵.

B. A = 2⁴.9⁵.

C. A = 4².3¹⁰.

D. A = 2⁴.3¹⁰.

Lời giải A = 4².9⁵ = 4.4.9.9.9.9.9 = 2.2.2.2.3.3.3.3.3.3.3.3.3.3 = 2⁴.3¹⁰.

Đáp án: D

Câu 16. Chọn câu sai:

A. 504 = 2³.3².7.

B. 102 = 2.3.17.

C. 75 = 2.5².

D. 170 = 2.5.17.

Lời giải

Vậy 504 = 2³.3².7 nên A đúng.

Vậy 102 = 2.3.17 nên B đúng

Vậy 75 = 3.5² nên C sai.

Vậy 170 = 2.5.17 nên D đúng.

Đáp án: C

Câu 17. Tìm các số còn thiếu trong sơ đồ phân tích một số ra thừa số nguyên tố sau:

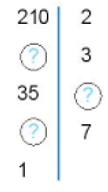
Các số cần điền từ lần lượt từ trên xuống dưới là:

A. 105; 5 và 7.

B. 105; 7 và 5.

C. 150; 5 và 7.

D. 150; 7 và 5.

Lời giải

+) Ta có 210 : 2 = 105

                    105 : 3 = 35

                    35 : 5 = 7

                    7 : 7 = 1

Ta hoàn thiện sơ đồ:             

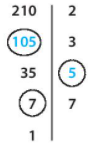
Vậy các số còn thiếu lần lượt từ trên xuống dưới là: 105; 5 và 7.

Đáp án: A

Câu 18. Tìm các số thích hợp điền vào ô trống trong sơ đồ sau: 

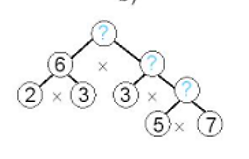
Các số cần điền lần lượt từ trên xuống dưới là:

A. 630; 35; 105.

B. 35; 105; 630.

C. 630; 105; 35.

D. 35; 630; 105.

Lời giải

Ta có: 5 x 7 = 35;

35 x 3 = 105;

105 x 6 = 630.

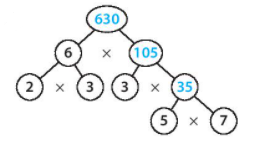
Vậy các số cần điền từ trên xuống dưới lần lượt là: 630; 105 và 35.

Đáp án: B

Câu 19. Phân tích 70 ra thừa số nguyên tố ta được: 70 = 2^x.5^y.7^z. Tổng x + y + z = ?

A. 3;

B. 4;

C. 5;

D. 6.

Lời giải

Ta có:

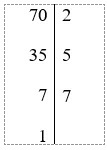
Vậy 70 = 2.5.7.

Suy ra x = 1; y = 1; z = 1.

Do đó x + y + z = 1 + 1 + 1 = 3.

Đáp án: A