Tailieumoi.vn xin giới thiệu Bài tập Toán lớp 6 Dấu hiệu chia hết, được sưu tầm và biên soạn theo chương trình học của 3 bộ sách mới. Bài viết gồm 20 bài tập với đầy đủ các mức độ và có hướng dẫn giải chi tiết sẽ giúp học sinh ôn luyện kiến thức và rèn luyện kĩ năng làm bài tập Toán 6. Ngoài ra, bài viết còn có phần tóm tắt nội dung chính lý thuyết Dấu hiệu chia hết. Mời các bạn đón xem:
Bài tập Toán 6 Dấu hiệu chia hết
A. Bài tập Dấu hiệu chia hết
Bài 1. Từ ba số 2; 3; 7. Hãy ghép thành các số có ba chữ số khác nhau và chia hết cho 2.
Hướng dẫn giải
Số được ghép thành chia hết cho 2 nên phải có chữ số hàng đơn vị là 2.
Hai chữ số hàng chục có thể là 3 hoặc 7.
- Nếu chữ số hàng chục là 3 thì chữ số hàng trăm là 7.
Ta được số cần tìm là 732.
- Nếu chữ số hàng chục là 7 thì chữ số hàng trăm là 3.
Ta được số cần tìm là 372.
Vậy có hai số có thể ghép thành là 372 và 732.
Bài 2. Tìm b để số 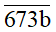
Hướng dẫn giải
Để 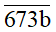
Để 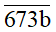
Do đó để 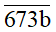
Vậy để 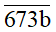
Bài 3. Có bao nhiêu số có hai chữ số chia hết cho 5.
Hướng dẫn giải
Các số có hai chữ số chia hết cho 5 là: 10; 15; 20; ….; 95.
Số các số có hai chữ số chia hết cho 5 là:
(95 – 10) : 5 + 1 = 18 (số)
Vậy có 18 số có hai chữ số chia hết cho 5.
Bài 4. Cho các số 82, 980, 5 975, 49 173, 756 598. Trong các số đó:
a) Số nào chia hết cho 5, nhưng không chia hết cho 2?
b) Số nào chia hết cho 2, nhưng không chia hết cho 5?
c) Số nào không chia hết cho 2 và không chia hết cho 5?
Lời giải:
a) Số chia hết cho 5 nhưng không chia hết cho 2 có chữ số tận cùng là 5.
Nên trong các số đã cho, số chia hết cho 5 nhưng không chia hết cho 2 là: 5 975.
b) Số chia hết cho 2 nhưng không chia hết cho 5 có chữ số tận cùng là 2; 4; 6; 8.
Nên trong các số đã cho, các số chia hết cho 2 nhưng không chia hết cho 5 là: 82; 756 598.
c) Số không chia hết cho 2 và không chia hết cho 5 thì không có tận cùng là 0; 2; 4; 5; 6; 8, hay nói cách khác là các số có chữ số tận cùng là 1; 3; 7; 9 thì không chia hết cho cả 2 và 5.
Do đó, trong các số đã cho số không chia hết cho 2 và không chia hết cho 5 là: 49 173.
Bài 5. Cho số N = 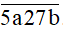 Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.
Có bao nhiêu số N sao cho N là số có 5 chữ số khác nhau và N chia cho 5 dư 1 và N chia hết cho 2.
Lời giải:
Điều kiện: a, b ∈ {0; 1; 2; 3; ....; 9}
N = 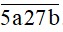 chia cho 5 dư 1 nên b ∈ {1; 6}
chia cho 5 dư 1 nên b ∈ {1; 6}
Mà N chia hết cho 2 nên b = 6, ta được số N = 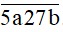
Lại có N là số có 5 chữ số khác nhau nên a ∈ {0; 1; 3; 4; 8; 9}
Vậy có 6 số N thỏa mãn yêu cầu bài là 50 276; 51 276; 53 276; 54 276; 58 276; 59 276.
Bài 6. Cho 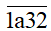
Hướng dẫn giải
Tổng các chữ số của 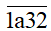
Nên để 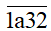
Do a là các số tự nhiên từ 0 đến 9 nên:
0 + 6 ≤ a + 6 ≤ 9 + 6.
Hay 6 ≤ a + 6 ≤ 15.
Số chia hết cho 9 từ 6 đến 15 chỉ có đúng một số là 9 nên a + 6 = 9
Do đó a = 3.
Vậy số thay thế cho a chỉ có thể là 3.
Bài 7: Cho 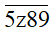
Hướng dẫn giải
Vì một số bất kỳ nếu chia hết cho 9 thì cũng chia hết cho 3 nên ta chỉ xét 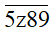
Để 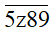
Hay (22 + z) ⋮ 9 nên z = 5.
Vậy với z = 5 thì 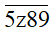
Bài 8. Tổng (hiệu) sau chia hết cho 3 hay 9?
a) 1251 + 5316;
b) 5436 – 1324;
c) 1 . 2 . 3 . 4 . 5 . 6 + 27.
Hướng dẫn giải
a) Tổng các chữ số của 1251 là 1 + 2 + 5 + 1 = 9 chia hết cho 3 và 9.
Tổng các chữ số của 5 316 là 5 + 3 + 1 + 6 = 15 chia hết cho 3 nhưng không chia hết cho 9.
Vậy 1251 + 5316 chia hết cho 3 nhưng không chia hết cho 9.
b) Tổng các chữ số của 5436 có 5 + 4 + 3 + 6 = 18 chia hết cho 3 và 9.
Tổng các chữ số của 1324 có 1 + 3 + 2 + 4 = 10 không chia hết cho 3 và 9.
Vậy 5436 – 1324 không chia hết cho 3 và 9.
c) Tích 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 (vì tích này có thừa số là 3).
Ta có: 1 . 2 . 3 . 4 . 5 . 6
= 1 . 2 . 3 . 4 . 5 . (3 . 2)
= 1 . 2 . 4 . 5 . (3 . 3) . 2
= 1 . 2 . 4 . 5 . 9 . 2 chia hết cho 9 (vì nó có thừa số là 9).
Do đó 1 . 2 . 3 . 4 . 5 . 6 chia hết cho 3 và 9.
Tổng các chữ số của 27 là 2 + 7 = 9 chia hết cho 3 và 9.
Vậy 1 . 2 . 3 . 4 . 5 . 6 + 27 chia hết cho 3 và 9.
Bài 9. Cho các số 104, 627, 3 114, 5 123, 6 831 và 72 102. Trong các số đó:
a) Số nào chia hết cho 3? Vì sao?
b) Số nào không chia hết cho 3? Vì sao?
c) Số nào chia hết cho 9? Vì sao?
d) Số nào chia hết cho 3, nhưng không chia hết cho 9? Vì sao?
Lời giải:
Ta áp dụng dấu hiệu chia hết cho 3 và dấu hiệu chia hết cho 9 để thực hiện bài tập này.
a) Trong các số đã cho ta có:
+ Số 627 chia hết cho 3 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3.
+ Số 3 114 chia hết cho 3 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 3.
+ Số 6 831 chia hết cho 3 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 3.
+ Số 72 102 chia hết cho 3 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3.
b) Ta có:
+ Số 104 không chia hết cho 3 vì tổng các chữ số 1 + 0 + 4 = 5 không chia hết cho 3.
+ Số 5 123 không chia hết cho 3 vì tổng các chữ số 5 + 1 + 2 + 3 = 11 không chia hết cho 3.
c) Ta có:
+ Số 3 114 chia hết cho 9 vì tổng các chữ số 3 + 1 + 1 + 4 = 9 chia hết cho 9.
+ Số 6 831 chia hết cho 9 vì tổng các chữ số 6 + 8 + 3 + 1 = 18 chia hết cho 9.
d) Ta có:
+ Số 627 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 6 + 2 + 7 = 15 chia hết cho 3 nhưng không chia hết cho 9.
+ Số 72 102 chia hết cho 3 và không chia hết cho 9 vì tổng các chữ số 7 + 2 + 1 + 0 + 2 = 12 chia hết cho 3 nhưng không chia hết cho 9.
Bài 10. Chứng minh rằng tích của 3 số tự nhiên liên tiếp luôn chia hết cho 3.
Lời giải:
Gọi 3 số tự nhiên liên tiếp là n; n + 1; n + 2 (với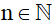 )
)
Tích của ba số tự nhiên liên tiếp là n(n + 1)(n + 2)
Mọi số tự nhiên n khi chia cho 3 có thể nhận số dư là 0, 1, 2.
+ Nếu r = 0 thì n chia hết cho 3. Khi đó n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 1 thì n có dạng n = 3k + 1 (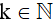 )
)
Ta có: n + 2 = 3k + 1 + 2 = 3k + 3 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
+ Nếu r = 2 thì n có dạng n = 3k + 2 (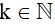 )
)
Khi đó: n + 1 = 3k + 2 + 1 = 3(k + 1) chia hết cho 3.
Do đó: n(n + 1)(n + 2) chia hết cho 3.
Vậy tích của ba số tự nhiên liên tiếp chia hết cho 3.
Câu 11. Trong các số sau số nào chia hết cho 3: 421; 248; 2 020; 2025.
A. 421.
B. 248.
C. 2 020.
D. 2 025.
Lời giải
Ta có 4 + 2 +1 = 7 không chia hết cho 3 nên 421 không chia hết cho 3.
Ta có: 2 + 4 + 8 = 14 không chia hết cho 3 nên 248 không chia hết cho 3.
Ta có 2 + 0 + 2 + 0 = 4 không chia hết cho 3 nên 2 020 không chia hết cho 3.
Ta có: 2 + 0 + 2 +5 = 9 chia hết cho 3 nên 2 025 chia hết cho 3.
Đáp án: D
Câu 12. Phát biểu nào dưới đây là đúng?
A. Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
B. Các số có chữ số tận cùng là 3; 6; 9 thì chia hết cho 3.
C. Các số có chữ số tận cùng là 0; 2; 4; 6; 8 thì chia hết cho 5.
D. Các số có chữ số tận cùng là 0; 5 thì chia hết cho 5.
Lời giải
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9. Do đó A sai.
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3. Do đó B sai.
Các số có chữ số tận cùng là 0; 2; 4; 6 là các số chia hết cho 2. Do đó C sai.
Các số có chữ số tận cùng là 0 hoặc 5 là các số chia hết cho 5. Do đó D đúng
Đáp án: D
Câu 13. Trong các số sau số nào chia hết cho 2:
A. 102;
B. 1 443;
C. 305;
D. 909.
Lời giải
Các số chia hết cho 2 là các số có chữ số tận cùng là 0; 2; 4; 6; 8.
Ta thấy 102 có tận cùng bằng 2 nên 102 chia hết cho 2.
Đáp án: A
Câu 14. Trong các số: 10 203; 450; 305; 194 724; 234 500. Có bao nhiêu số chia hết cho 5.
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Các số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5 là: 450; 305 và 234 500.
Vậy có 3 số chia hết cho 5.
Đáp án: D
Câu 15. Trong các số: 102; 355; 270; 2 350; 6 708. Số nào chia hết cho cả 2 và 5.
A. 102 và 270.
B. 355 và 2 350.
C. 270 và 2 350.
D. 355 và 6 708.
Lời giải Số vừa chia hết cho 2 và 5 là số có tận cùng bằng 0.
Đáp án: C
Câu 16. Từ các chữ số 5; 0; 4; 2. Viết các số tự nhiên có ba chữ số khác nhau sao cho mỗi số đó chia hết cho 3.
A. 2;
B. 4;
C. 6;
D.8.
Lời giải
Ta có: 5 + 0 + 4 = 9 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 504; 540; 405; 450.
Ta có: 0 + 4 + 2 = 6 chia hết cho 3 nên các số có ba chữ số khác nhau chia hết cho 3 lập từ ba chữ số này là: 402; 420; 240; 204.
Vậy có tất cả 8 số.
Đáp án: D
Câu 17. Cho số . Ta có thể thay a bởi bao nhiêu chữ số để số chia hết cho 3.
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Ta có: 3 + 2 + a + 3 = 8 + a.
Để số chia hết cho 3 thì 8 + a phải chia hết cho 3.
Suy ra a = 1; a = 4.
Vậy có 2 giá trị của a để số chia hết cho 3.
Đáp án: C
Câu 18. Trong các phát biểu dưới đây, có bao nhiêu phát biểu đúng?
I) Số có chữ số tận cùng là 4 thì chia hết cho 2.
II) Số chia hết cho 2 thì có chữ số tận cùng là 4.
III) Số vừa chia hết cho 2 vừa chia hết cho 5 thì có chữ số tận cùng là 0.
IV) Số chia hết cho 5 thì có chữ số tận cùng là 5.
A. 1;
B. 2;
C. 3;
D. 4.
Lời giải
Số có chữ số tận cùng là 4 thì chia hết cho 2. Suy ra (I) đúng.
Số chia hết cho 2 có thể có chữ số tận cùng là các số 0; 2; 4; 6; 8 không nhất thiết là số 4. Suy ra (II) sai.
Số vừa chia hết cho 2 vừa chia hết cho 5 thì có chữ số tận cùng là 0. Suy ra (III) đúng.
Số chia hết cho 5 có chữ số tận cùng là 0 hoặc 5 không chỉ mỗi số 5. Suy ra (IV) sai.
Vậy có 2 phát biểu đúng.
Đáp án: B
Câu 19. Không thực hiện phép tính, em hãy cho biết phát biểu nào là đúng.
A. 1 953 + 1 975 chia hết cho 9.
B. 2 020 – 938 chia hết cho 2.
C. 1 942 – 1 930 chia hết cho 5.
D. 2 225 + 1 113 chia hết cho 3.
Lời giải
Ta có 1 + 9 + 5 + 3 = 18 chia hết cho 9 nên 1 953 chia hết cho 9, nhưng 1 + 9 + 7 + 5 = 22 không chia hết cho 9 nên 1 975 không chia hết cho 9.
Suy ra 1 953 + 1 975 không chia hết cho 9. Do đó A sai.
2 020 và 938 là số có chữ số tận cùng lần lượt là 0 và 8 nên cả hai số đều chia hết cho 2.
Suy ra 2 020 – 938 chia hết cho 2. Do đó B đúng.
Ta có 1 942 có tận cùng là 2 không chia hết cho 5, còn 1 930 có tận cùng là 0 nên chia hết cho 5. Như vậy 1 942 – 1 930 không chia hết cho 5. Do đó C sai.
Ta có 2 + 2 + 2 + 5 = 11 không chia hết cho 3, 1 + 1 + 1 + 3 = 6 chia hết cho 3.
Suy ra 2 225 + 1 113 chia hết cho 3. Do đó D sai.
Đáp án: B
Câu 20. Tìm x, y để số vừa chia hết cho 5, vừa chia hết cho 9.
A. x = 1; y = 0;
B. x = 3; y = 5;
C. Cả A và B đều đúng;
D. Cả A và B đều sai.
Lời giải
Để số đó chia hết cho 5 thì chữ số tân cùng là 0 hoặc 5.
+) y = 0
Khi đó số đã cho là có tổng các chữ số: 3 + x + 5 + 0 = 8 + x.
Để số này chia hết cho 9 thì 8 + x phải chia hết cho 9.
Suy ra x = 1, x = 10, …
Vì x và y là các chữ số nên x và y thuộc nên x = 1.
Vậy x =1; y = 0.
+) y = 5
Khi đó số đã cho là có tổng các chữ số: 3 + x + 5 + 5 = 13 + x.
Để số này chia hết cho 9 thì 13 + x phải chia hết cho 9.
Suy ra x = 5, x = 14, …
Vì x và y là các chữ số nên x và y thuộc nên x = 5.
Vậy x = 5, y = 5.
Đáp án: C
Câu 21. Dùng ba chữ số 3; 0; 4 để viết các số có ba chữ số khác nhau chia hết cho 2. Hỏi có bao nhiêu số như vậy?
A. 6.
B. 4.
C. 2.
D. 0.
Lời giải
Số chia hết cho 2 thì chữ số tận cùng chỉ có thể là 0 hoặc 4.
Nên các số ba chữ số khác nhau lập từ ba chữ số 3; 0; 4 mà chia hết cho 2 là: 304; 340.
Vậy có 2 số như vậy.
Đáp án: C
Câu 22. Trên một bờ đất dài 108m, một bác nông dân có kế hoạch trồng một số cây dừa thành một hàng sao cho hai cây cách đều nhau là 9m và luôn có cây ở vị trí đầu và cuối của bờ đất. Hỏi bác nông dân có trồng được như vậy không? Nếu được, bác cần bao nhiêu cây dừa để trồng?
A. 12;
B. 13;
C. 10;
D. 11
Lời giải
Ta thấy 108 có tổng các chữ số là 1 + 0 + 8 = 9 9 nên 108 9
Mà hai cây cách đều nhau 9m vì thế mà bác nông dân trồng được như vậy.
Vì cứ 2 cây dừa liên tiếp có 1 khoảng cách là 9m, 3 cây dừa liên tiếp có 2 khoảng cách, … nên số các khoảng cách giữa hai cây liên tiếp là:
108 : 9 = 12 (khoảng cách)
Số cây dừa bác cần để trồng là:
12 + 1 = 13 (cây)
Vậy bác cần trồng 13 cây dừa.
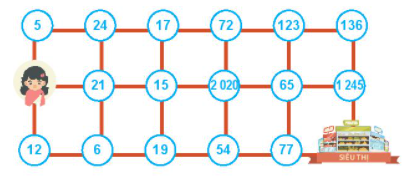
Câu 23. Bạn Hà cần tìm đường đến siêu thị. Biết rằng Hà chỉ có thể đi qua ô có chứa số chia hết cho 2 hoặc chia hết cho 3 và mỗi ô chỉ đi qua một lần. Em hãy giúp Hà đến được siêu thị nhé. Hỏi có mấy cách để Hà đến siêu thị?
A. 0;
B. 1;
C. 2;
D. 3.
Lời giải
Vì Hà chỉ có thể đi qua ô chứa số chia hết cho 2 hoặc 3 nên Hà không thể đi qua các ô số:
5; 17; 19; 65; 77 vì các ô số này đều không chia hết cho 2 và 3.
Có nhiều cách để Hà đi đến siêu thị, dưới đây là 2 cách:
Cách 1: Hà → 21 → 15 → 2020 → 72 → 123 → 136 → 1245 → siêu thị
Cách 2: Hà → 12 → 6 → 21 → 15 → 2020 → 72 → 123 → 136 → 1245 → siêu thị.
Đáp án: C
Câu 24. Có 162 học sinh tham gia chương trình đào tạo bóng đá, được chia thành các đội. Mỗi đội cần có 9 học sinh. Nhận xét nào dưới đây là đúng.
A. Có một đội không đủ 9 học sinh.
B. Có hai một không đủ 9 học sinh.
C. Có ba đội không đủ 9 học sinh.
D. Không có đội nào không đủ 9 học sinh.
Lời giải Tổng các chữ số của 162 là 1 + 6 + 2 = 9 chia hết cho 9 nên 162 chia hết cho 9. Do đó chia 162 em học sinh thành các đội, thì không có đội nào không đủ 9 học sinh.
Đáp án: D
B. Lý thuyết Dấu hiệu chia hết
1. Dấu hiệu chia hết cho 2
Các số có chữ số tận cùng là 0; 2; 4; 6; 8 (tức là chữ số chẵn) thì chia hết cho 2 và chỉ những số đó mới chia hết cho 2.
Ví dụ:
a) Số 15 552 chia hết cho 2 vì có chữ số tận cùng là 2.
b) Số 955 không chia hết cho 2 vì có chữ số tận cùng là 5 (5 không là số chẵn).
2. Dấu hiệu chia hết cho 5
Các số có chữ số tận cùng là 0 hoặc 5 thì chia hết cho 5 và chỉ những số đó mới chia hết cho 5.
Ví dụ: Xét số 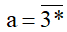
Hướng dẫn giải
Chữ số tận cùng của a là ∗ nên để a chia hết cho 5 thì ∗ phải là 0 hoặc 5.
Để a không chia hết cho 5 thì ∗ phải khác 0 hoặc 5, tức là các số 1; 2; 3; 4; 6; 7; 8; 9.
Vậy thay ∗ bằng 1; 2; 3; 4; 6; 7; 8; 9 thì a không chia hết cho 5.
3. Dấu hiệu chia hết cho 3
Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.
Ví dụ:
+ Số 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 thì số 102 chia hết cho 3.
+ Số 321 có tổng các chữ số là 3 + 2 + 1 = 6 chia hết cho 3 thì số 321 chia hết cho 3.
4. Dấu hiệu chia hết cho 9
Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.
Ví dụ:
+ Số 792 có tổng các chữ số là 7 + 9 + 2 = 18 chia hết cho 9 thì số 792 chia hết cho 9.
+ Số 108 có tổng các chữ số là 1 + 0 + 8 = 9 chia hết cho 9 thì số 108 chia hết cho 9.