Với giải sách bài tập Toán 6 Bài 5: Phép nhân các số nguyên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 5: Phép nhân các số nguyên
Bài 40 trang 81 sách bài tập Toán lớp 6 Tập 1: Thực hiện phép tính:
a) (-6).9; b) (-12).(-987);
c) 90.(-108).(-3); d) 29.(-78).(-9).(-11);
e) 6.(-4)2.(-10)2 + 52; f) (-7).(-7).(-7) + 73;
h) (-103).(-102) – 132; i) (-8).(-8).(-8).(-8) – 84 + 105.
Lời giải:
a) (-6).9
= -6.9
= -54.
b) (-12).(-987)
= 12.987
= 11 844.
c) 90.(-108).(-3)
= (-9 720).(-3)
= 29 160.
d) 29.(-78).(-9).(-11)
= (-2 262).(-9).(-11)
= 20 358.(-11)
= - 223 938.
e) 6.(-4)2.(-10)2 + 52
= 6.16.100 + 25
= 9 600 + 25
= 9 625.
f) (-7).(-7).(-7) + 73
= - 73 + 73
= 73 – 73
= 0.
h) (-103).(-102) – 132
= (-1 000).(-100) – 169
= 100 000 – 169
= 99 831.
i) (-8).(-8).(-8).(-8) – 84 + 105
= 84 – 84 + 105
= 0 + 105
= 105.
Bài 41 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn các dấu “+”, “-“ thích hợp cho 
:
|
a |
b |
Dấu của a.b |
|
+ |
- |
? |
|
- |
+ |
? |
|
- |
- |
? |
|
+ |
+ |
? |
Lời giải:
+) a mang dấu dương, b mang dấu âm suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.
+) a mang dấu âm, b mang dấu dương suy ra a và b là hai số nguyên trái dấu. Do đó tích a.b mang dấu âm.
+) a mang dấu âm, b mang dấu âm suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.
+) a mang dấu dương, b mang dấu dương suy ra a và b là hai số nguyên cùng dấu. Do đó tích a.b mang dấu dương.
Khi đó ta có bảng sau:
|
a |
b |
Dấu của a.b |
|
+ |
- |
- |
|
- |
+ |
- |
|
- |
- |
+ |
|
+ |
+ |
+ |
Bài 42 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn số thích hợp cho 
:
|
a |
-23 |
221 |
? |
-25 |
12 |
|
b |
-9 |
-45 |
399 |
? |
? |
|
c |
2 |
? |
0 |
-1 |
-38 |
|
a.b |
? |
? |
1 197 |
-100 |
-156 |
|
c(a + b) |
? |
176 |
? |
? |
? |
Lời giải:
+) Với a = -23, b = -9, c = 2 thì:
a.b = (-23).(-9) = 207;
c(a + b) = 2.[(-23) + (-9)] = 2.(-32) = -64.
+) Với a = 221, b = -45, c(a + b) = 176 thì:
a.b = 221.(-45) = -9 945;
Ta có: c(a + b) = 176
c.[221 + (-45)] = 176
c.176 = 176
c = 1.
+) Với b = 399, c = 0, a.b = 1 197. Khi đó:
Ta có: a.b = 1 197
a.399 = 1 197
a = 1 197:399
a = 3;
c.(a + b) = 0.(399 + 3) = 0.402 = 0.
+) Với a = -25, c = -1 và a.b = -100. Khi đó:
Ta có: a.b = -100
(-25).b = -100
(-25).b = (-25).4
b = 4.
c(a + b) = (-1).[(-25) + 4] = (-1).(-21) = 21.
+) Với a = 12, c = -38, a.b = -156. Khi đó:
Ta có: a.b = -156
12.b = -156
12.b = 12.(-13)
b = -13;
c(a + b) = (-38).[12 + (-13)] = (-38).(-1) = 38.
Từ đó, ta có bảng sau:
|
a |
-23 |
221 |
3 |
-25 |
12 |
|
b |
-9 |
-45 |
399 |
4 |
-13 |
|
c |
2 |
1 |
0 |
-1 |
-38 |
|
a.b |
207 |
-9 945 |
1 197 |
-100 |
-156 |
|
c(a + b) |
-64 |
176 |
0 |
21 |
38 |
Bài 43 trang 82 sách bài tập Toán lớp 6 Tập 1: Tính giá trị của biểu thức trong mỗi trường hợp sau:
a) 19x với x = - 7;
b) 28xy với x = -12 và y = -15;
c) 29m – 58n với m = -2 và n = 3;
d) (- 2021)abc + ab với a = -21, b = -11 và c = 0.
Lời giải:
a) Thay x = -7 vào 19x, ta được:
19.(-7) = -133.
Vậy với x = -7 thì giá trị biểu thức là -133.
b) Thay x = -12 và y = -15 vào biểu thức 28xy, ta được:
28.(-12).(-15) = (-336).(-15) = 5 040.
Vậy với x = -12 và y = -15 thì giá trị biểu thức là 5 040.
c) Thay m = -2 và n = 3 vào 29m – 58n, ta được:
29.(-2) – 58.3
= (-58) – 58.3
= (-58) + (-58).3
= (-58).(1 + 3)
= (-58).4
= -232.
Vậy với m = -2 và n = 3 thì giá trị biểu thức là -232.
d) Thay a = -21, b = -11 và c = 0 vào biểu thức (- 2021)abc + ab, ta được:
(- 2021)(-21).(-11).0 + (-21).(-11)
= 0 + 231
= 231.
Vậy với a = -21, b = -11 và c = 0 thì giá trị biểu thức là 231.
Bài 44 trang 82 sách bài tập Toán lớp 6 Tập 1: Chọn dấu “<”, “>”, “=” thích hợp cho dấu 
:
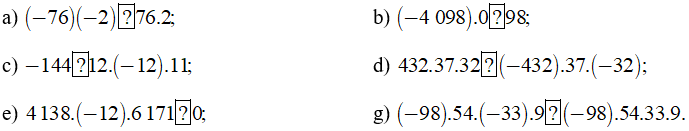
Lời giải:
a) Ta có (-76).(-2) = 76.2. Do đó ta điền: (-76)(-2)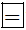 
76.2
b) Ta có (-4 098).0 = 0 < 98. Do đó ta điền: (-4 098) : 0 
98
c) Ta có 12.(-12).11 = (-144).11 = -1 584 < -144. Do đó ta điền: -144 
12.(-12).11
d) Ta có: (-432).37.(-32) =-(432.37).(-32) = 432.37.32. Do đó ta điền: 432.37.32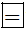 
(-432).37.(-32)
e) 4 138.(-12).6 171 = -(4 138.12).6 171 = -(4 138.12.6 171) < 0. Do đó ta điền: 4138.(-12).6171 
0
g) Ta có: (-98).54.(-33).9 = 98.54.33.9, (-98).54.33.9 = -(98.54.33.9).
Vì -(98.54.33.9) < 98.54.33.9 nên (-98).54.33.9 < (-98).54.(-33).9. Do đó ta điền: (-98).54.(-33).9 
(-98).54.33.9
Bài 45 trang 82 sách bài tập Toán lớp 6 Tập 1: Tính một cách hợp lí:
a) (-16).(-9).5;
b) (-15).999;
c) (-25).144.(-4);
d) (-125).2 020.(-8);
e) (-2 021).(-15) + (-15).2 020;
g) 121.(-63) + 63.(-53) – 63.26.
Lời giải:
a) (-16).(-9).5
= [(-16).5].(-9)
= (-80).(-9)
= 720.
b) (-15).999
= (-15)(1 000 – 1)
= (-15).1 000 – (-15).1
= -15 000 + 15
= -(15 000 – 15)
= -14 985.
c) (-25).144.(-4)
= [(-25).(-4)].144
= 100.144
= 14 400.
d) (-125).2 020.(-8)
= [(-125).(-8)].2 020
= 1 000.2 020
= 2 020 000.
e) (-2 021).(-15) + (-15).2 020
= (-15).[(-2 021) + 2 020]
= (-15).(-1)
= 15.
g) 121.(-63) + 63.(-53) – 63.26
= 121.(-63) + (-63).53 + (-63).26
= (-63).(121 + 53 + 26)
= (-63).200
= -12 600.
|
Tháng |
Lợi nhuận (triệu đồng) |
|
Tháng 1 |
50 |
|
Tháng 2 |
-10 |
|
Tháng 3 |
50 |
|
Tháng 4 |
40 |
|
Tháng 5 |
-20 |
|
Tháng 6 |
-10 |
Sau 6 tháng đầu năm, công ty Bình An kinh doanh lãi hay lỗ với số tiền là bao nhiêu?
Lời giải:
Số tiền của công ty Bình An thu được sau 6 tháng đầu năm là:
50 + (-10) + 50 + 40 + (-20) + (-10) = 100 (triệu đồng)
Vậy sau 6 tháng đầu năm, công tu Bình An kinh doanh lãi 100 triệu đồng.
a) (- 2021).2 021 và (-2 020).2 022;
b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.
Lời giải:
a) Ta có: (- 2021).2 021
= [(-2 020) + (-1)].2 021
= (-2 020).2 021 + (-1).2 021
= (-2 020).2 021 + (-2 021)
Ta có: (-2 020).2 022 = (-2 020)(2 021 + 1) = (-2 020).2 021 + (-2 020).
Vì -2 021 < -2 020 nên (-2 020).2 021 + (-2 021) < (-2 020).2 021 + (-2 020) hay (- 2021).2 021 < (-2 020).2 022.
b) (8 765 – 5 678).[5 678 – 9 765 + (-12)] và 4 342.
Ta có 8 765 – 5 678 > 0, 5 678 – 9 765 + (-12) < 0.
Do đó (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 0 mà 4 342 > 0.
Vậy (8 765 – 5 678).[5 678 – 9 765 + (-12)] < 4 342.
Bài 48 trang 83 sách bài tập Toán lớp 6 Tập 1: Cho hai số nguyên x, y (x ≠ 0, y ≠ 0, x > y, x ≠ -y)
Gọi m = x2.y2.(x – y).(x + y)4. Hỏi m là số nguyên dương hay nguyên âm?
Lời giải:
Vì x > y nên x – y > 0.
Ta có x2 ≥ 0 với mọi x mà x ≠ 0 nên x2 > 0.
Ta có y2 ≥ 0 với mọi x mà y ≠ 0 nên y2 > 0.
Ta lại có x ≠ - y nên x + y ≠ 0 suy ra (x + y)4 > 0.
Do đó m = x2.y2.(x – y).(x + y)4 > 0.
Vậy m là một số nguyên dương.
Bài 49 trang 83 sách bài tập Toán lớp 6 Tập 1: Tìm các số nguyên x thỏa mãn:
a) 16x2 = 64; b) 25(x2 – 1) – 75 = 9 900;
c) (x – 6).(2x – 6) = 0; d) (5x – 10)(6x + 12) = 0.
Lời giải:
a) 16x2 = 64
x2 = 64:16
x2 = 4
x2 = 22 = (-2)2
x = 2 hoặc x = -2.
Vậy x = 2 hoặc x = -2.
b) 25(x2 – 1) – 75 = 9 900
25(x2 – 1) = 9 900 + 75
25(x2 – 1) = 9 975
x2 – 1 = 9 975:25
x2 – 1 = 9 975:25
x2 – 1 = 399
x2 = 400
x2 = 202 = (-20)2
x = 20 hoặc x = -20.
Vậy x = 20 hoặc x = -20.
c) (x – 6).(2x – 6) = 0
TH1: x – 6 = 0
x = 6.
TH2: 2x – 6 = 0
2x = 6
x = 3.
Vậy x = 6 hoặc x = 3.
d) (5x – 10)(6x + 12) = 0
TH1: 5x – 10 = 0
5x = 10
x = 2.
TH2: 6x + 12 = 0
6x = -12
6x = 6.(-2)
x = -2.
Vậy x = 2 hoặc x = -2.
Bài 50 trang 83 sách bài tập Toán lớp 6 Tập 1: Cho bảng gồm 2 015x2 015 ô vuông nhỏ (Hình 9).
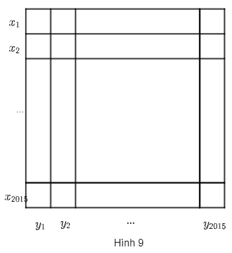
Điền vào mỗi ô của bảng số 1 hoặc số -1.
Bên trái mỗi dòng thứ i ghi tích các số của dòng đó và đặt là xi. Dưới mỗi cột thứ j ghi tích các số của cột đó và đặt là yj. (i = 1; 2; 3; …; 2 015 và j = 1; 2; 3; …; 2 015).
Chứng tỏ rằng tổng của 4 030 số xi,yj nhận được khác 0.
Lời giải:
Giả sử tổng của 4 030 số xi,yj bằng 0.
Ta có x1 + x2 + … + x2015 + y1 + y2 + … + y2015 = 0.
Mà mỗi số xi, yi đều bằng 1 hoặc -1 nên trong 4 030 số xi, yi có 2 015 số bằng -1 và 2 015 số bằng 1.
Do đó tích x1.x2…x2015.y1.y2…y2015 = - 1 (vì số các thừa số bằng -1 là lẻ). (1)
Mặt khác x1.x2…x2015 = y1.y2…y2015 (đều là tích của các số trong bảng).
Suy ra x1.x2…x2015.y1.y2…y2015 = (x1.x2…x2015)2 = 1. (mâu thuẫn với (1)).
Do đó giải sử sai.
Vậy tổng của 4 030 số xi,yj nhận được khác 0.
Lý thuyết Phép nhân các số nguyên
I. Phép nhân hai số nguyên khác dấu
Để nhân hai số nguyên khác dấu, ta làm như sau:
Bước 1. Bỏ dấu “–” trước số nguyên âm, giữ nguyên số nguyên còn lại
Bước 2. Tính tích của hai số nguyên dương nhận được ở Bước 1
Bước 3. Thêm dấu “–” trước kết quả nhận được ở Bước 2, ta có tích cần tìm.
Chú ý: Tích của hai số nguyên khác dấu là số nguyên âm.
Ví dụ: (– 6) . 7 = – (6 . 7) = – 42
20 . (– 10) = – (20 . 10) = – 200
II. Phép nhân hai số nguyên cùng dấu
1. Phép nhân hai số nguyên dương
Nhân hai số nguyên dương chính là nhân hai số tự nhiên khác 0.
Ví dụ: 4 . 6 = 24; 16 . 2 = 32.
2. Phép nhân hai số nguyên âm
Để nhân hai số nguyên âm, ta làm như sau:
Bước 1. Bỏ dấu “–” trước mỗi số
Bước 2. Tính tích của hai số nguyên dương nhận được ở Bước 1, ta có tích cần tìm.
Chú ý: Tích của hai số nguyên cùng dấu là số nguyên dương.
Ví dụ: (– 5) . (– 9) = 5 . 9 = 45
(– 20) . (– 6) = 20 . 6 = 120
Chú ý: Cách nhận biết dấu của tích
(+) . (+) → (+)
(–) . (–) → (+)
(+) . (–) → (–)
(–) . (+) → (–)
III. Tính chất của phép nhân các số nguyên
Giống như phép nhân các số tự nhiên, phép nhân các số nguyên cũng có các tính chất: giao hoán; kết hợp; nhân với số 1; phân phối của phép nhân đối với phép cộng, phép trừ.
+ Tính chất giao hoán: a . b = b . a
+ Tính chất kết hợp: (a . b) . c = a . (b . c)
+ Tính chất nhân với số 1: a . 1 = 1 . a = a
+ Tính chất phân phối của phép nhân đối với phép cộng: a . (b + c) = a . b + a . c
Tính chất phân phối của phép nhân đối với phép trừ: a . (b – c) = a . b – a . c
Chú ý:
a . 0 = 0 . a = 0
a . b = 0 thì hoặc a = 0 hoặc b = 0
Ví dụ: Tính
a) (– 9) . 4 . (– 5);
b) (– 127 086) . 674 . 0;
c) (– 4) . 7 + (– 4) . 3.
Lời giải:
a) (– 9) . 4 . (– 5) = (– 9) . [4 . (– 5)] = (– 9) . (– 20) = 9 . 20 = 180
b) (– 127 086) . 674 . 0 = 0
c) (– 4) . 7 + (– 4) . 3 = (– 4) . (7 + 3) = (– 4) . 10 = – 40
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
