Với giải sách bài tập Toán 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9 sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 9: Dấu hiệu chia hết cho 3, cho 9

Bài 77 trang 27 sách bài tập Toán lớp 6 Tập 1: Cho các số 27; 45; 881; 916; 2 100; 2 439; 13 118; 35 550; 5 223 411. Trong các số đó:

a) Số nào chia hết cho 3?

b) Số nào lớn hơn 2 000 không chia hết cho 3?

c) Số nào chia hết cho 9?

d) Số nào nhỏ hơn 3 000 không chia hết cho 9?

Lời giải:

a) Ta có: 2 + 7 = 9 chia hết cho 3 nên 27 chia hết cho 3;

Ta có: 4 + 5 = 9 chia hết cho 3 nên 45 chia hết cho 3;

Ta có: 8 + 8 + 1 = 17 không chia hết cho 3 nên 881 không chia hết cho 3;

Ta có: 9 + 1 + 6 = 16 không chia hết cho 3 nên 916 không chia hết cho 3;

Ta có: 2 + 1 + 0 + 0 = 3 chia hết cho 3 nên 2 100 chia hết cho 3;

Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 3 nên 2 439 chia hết cho 3;

Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 3 nên 13 118 không chia hết cho 3;

Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 3 nên 35 550 chia hết cho 3;

Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 3 nên 5 223 411 chia hết cho 3;

Vậy các số chia hết cho 3 là: 27; 45; 2 100; 2 439; 35 550; 5 223 411.

b) Các số còn lại là các số không chia hết cho 3 là: 881; 916; 13 118.

Trong các số này số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.

Vậy số lớn hơn 2 000 và không chia hết cho 3 là: 13 118.

c) Ta có: 2 + 7 = 9 chia hết cho 9 nên 27 chia hết cho 9;

Ta có: 4 + 5 = 9 chia hết cho 9 nên 45 chia hết cho 9;

Ta có: 8 + 8 + 1 = 17 không chia hết cho 9 nên 881 không chia hết cho 9;

Ta có: 9 + 1 + 6 = 16 không chia hết cho 9 nên 916 không chia hết cho 9;

Ta có: 2 + 1 + 0 + 0 = 3 không chia hết cho 9 nên 2 100 không chia hết cho 9;

Ta có: 2 + 4 + 3 + 9 = 18 chia hết cho 9 nên 2 439 chia hết cho 9;

Ta có: 1 + 3 + 1 + 1 + 8 = 14 không chia hết cho 9 nên 13 118 không chia hết cho 9;

Ta có: 3 + 5 + 5 + 5 + 0 = 18 chia hết cho 9 nên 35 550 chia hết cho 9;

Ta có: 5 + 2 + 2 + 3 + 4 + 1 + 1 = 18 chia hết cho 9 nên 5 223 411 chia hết cho 9;

Vậy các số chia hết cho 9 là: 27; 45; 2 439; 35 550; 5 223 411.

d) Các số không chia hết cho 9 mà nhỏ hơn 3 000 là: 881; 916; 2 100.

Bài 78 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x để số 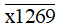 thỏa mãn mỗi điều kiện sau:

a) Chia hết cho 3;

b) Chia hết cho 9; 

c) Chia hết cho 3, nhưng không chia hết cho 9.

Lời giải:

Ta có x + 1 + 2 + 6 + 9 = x + 18.

a) Để số đã cho chia hết cho 3 thì x + 18 chia hết cho 3.

Khi đó x ∈ {0;3;6;9;12...}.

Mà x là chữ số và x khác 0 nên x ∈ {3;6;9}.

Vậy x ∈ {3;6;9}.

b) Để số đã cho chia hết cho 9 thì x + 18 chia hết cho 9.

Khi đó x ∈ {0;9;18;...}.

Mà x là chữ số và x khác 0 nên x = 9.

Vậy x = 9.

c) Để số đã cho chia hết cho 3, nhưng không chia hết cho 9 thì x + 18 chia hết cho 3, nhưng không chia hết cho 9.

Khi đó x ∈ {3;6;12;15...}.

Mà x là chữ số nên x ∈ {3;6}.

Vậy x ∈ {3;6}.

Bài 79 trang 27 sách bài tập Toán lớp 6 Tập 1: Có bao nhiêu số có dạng  chia cho 5 dư 1 và chia hết cho 9?

Lời giải:

Để số 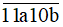 chia cho 5 dư 1 thì b ∈ {1;6}.

TH1: b = 1

Ta có: 1 + 1 + a + 1 + 0 + 1 = a + 4 

Để số 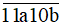 chia hết cho 9 thì a + 4 chia hết cho 9 mà a là chữ số nên a = 5.

Suy ra 115 101 thỏa mãn chia 5 dư 1 và chia hết cho 9.

TH2: b = 6

Ta có: 1 + 1 + a + 1 + 0 + 6 = a + 9

Để số 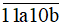 chia hết cho 9 thì a + 9 chia hết cho 9 mà a là chữ số nên a = 0 hoặc a = 9.

Suy ra 110 106 và 119 106 thỏa mãn chia cho 5 dư 1 và chia hết cho 9.

Vậy có ba số chia hết cho 9, chia 5 dư 1.

Bài 80 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 3:

a) A = 1 233 + 42 312 + 72 036;

b) B = 111 + 222 + 333 + … + 999.

Lời giải:

a) Ta có: 1 + 2 + 3 + 3 = 9 chia hết cho 3 nên 1 223 chia hết cho 3;

Ta có: 4 + 2 + 3 + 1 + 2 = 12 chia hết cho 3 nên 42 312 chia hết cho 3;

Ta có: 7 + 2 + 0 + 3 + 6 = 18 chia hết cho 3 nên 72 036 chia hết cho 3;

Do đó: 1 233 + 42 312 + 72 036 chia hết cho 3.

Vậy A = 1 233 + 42 312 + 72 036 chia hết cho 3.

b) B = 111 + 222 + 333 + … + 999

= 111 + 2.111 + 3.111 + … + 9.111

= 111.(1 + 2 + 3 + … + 9)

Ta có: 1 + 1 + 1 = 3 chia hết cho 3 nên 111 chia hết cho 3.

Do đó 111.(1 + 2 + 3 + … + 9) chia hết cho 3.

Vậy B = 111 + 222 + 333 + … + 999 chia hết cho 3.

Bài 81 trang 27 sách bài tập Toán lớp 6 Tập 1: Không tính giá trị biểu thức, hãy giải thích tại sao mỗi biểu thức sau chia hết cho 9:

a) P = 81 + 108 + 918;

b) M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312;

c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021.

Lời giải:

a) Ta có: 8 + 1 = 9 chia hết cho 9 nên 81 chia hết cho 9;

Ta có: 1 + 0 + 8 = 9 chia hết cho 9 nên 108 chia hết cho 9;

Ta có: 9 + 1 + 8 = 18 chia hết cho 9 nên 918 chia hết cho 9;

Do đó: 81 + 108 + 918 chia hết cho 9.

Vậy P = 81 + 108 + 918 chia hết cho 9.

b) Ta có: 5 + 8 + 5 =18 chia hết cho 9 nên 585 chia hết cho 9. Do đó 12.585 chia hết cho 9.

Ta có: 6 + 3 + 3 + 3 + 3 = 18 chia hết cho 9 nên 63 333 chia hết cho 9. Do đó 13.63 333 chia hết cho 9.

Ta có: 3 + 7 + 8 + 2 + 2 + 5 = 27 chia hết cho 9 nên 378 225 chia hết cho 9. Do đó 14. 378 225 chia hết cho 9

Ta có: 5 + 1 + 4 + 2 + 3 + 1 + 2 = 18 chia hết cho 9 nên 5 142 312 chia hết cho 9. Do đó 18.5 142 312 chia hết cho 9.

Vậy M = 12.585 + 13.63 333 + 14. 378 225 + 18.5 142 312 chia hết cho 9.

c) N = 11 + 22 + 33 + … + 99 + 2 021.60 021

= (11 + 88) + (22 + 77) + (33 + 66) + (44 + 55) + 99 + 2 021.60 021

= 99 + 99 + 99 + 99 + 99 + 2 021.60 021.

Ta có: 9 + 9 = 18 chia hết cho 9 nên 99 chia hết cho 9;

6 + 0 + 0 + 2 + 1 = 9 chia hết cho 9 nên 60 021 chia hết cho 9. Do đó 2 021.60 021 chia hết cho 9.

Suy ra 99 + 99 + 99 + 99 + 99 + 2 021.60 021 chia hết cho 9.

Vậy N = 11 + 22 + 33 + … + 99 + 2 021.60 021 chia hết cho 9.

Bài 82 trang 27 sách bài tập Toán lớp 6 Tập 1: Tìm các số tự nhiên a, b sao cho:

a) 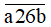 chia hết cho cả 2, 3, 5 và 9;

b) 123.a + 9 873.b = 2 227 691.

Lời giải:

a) Để số chia hết cho 2, 5 thì b = 0;

Khi đó số cần tìm là: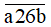 

Ta có: a + 2 + 6 + 0 = a + 8;

Để số 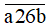 chia hết cho 3 và 9 thì a + 8 chia hết cho 3 và 9.

Mà a là chữ số và a khác 0 nên a = 1.

Vậy a = 1, b = 0 thì số 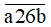 chia hết cho cả 2, 3, 5 và 9.

b) Ta có 1 + 2 + 3 = 6 chia hết cho 3 nên 123 chia hết cho 3. Do đó 123.a chia hết cho 3.

Ta có: 9 + 8 + 7 + 3 = 27 chia hết cho 3 nên 9 873 chia hết cho 3. Do đó 9 873.b chia hết cho 3.

Vì vậy 123.a + 9 873.b chia hết cho 3.

Ta lại có: 2 + 2 + 2 + 7 + 6 + 9 + 1 = 29 không chia hết cho 3.

Do đó không tồn tại a và b thỏa mãn yêu cầu bài toán.

Bài 83 trang 27 sách bài tập Toán lớp 6 Tập 1:

a) Có bao nhiêu số tự nhiên có hai chữ số chia cho 3 dư 1?

b) Có bao nhiêu số tự nhiên có ba chữ số chia cho 9 dư 2?

c) Có bao nhiêu số tự nhiên có hai chữ số 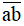 sao cho  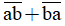chia hết cho 9?

Lời giải:

a) Các số tự nhiên có hai chữ số chia cho 3 dư 1 là: 10; 13; …; 97.

Số các số tự nhiên có hai chữ số chia cho 3 dư 1 là: (97 – 10):3 + 1 = 30 số.

Vậy có 30 số tự nhiên có hai chữ số chia cho 3 dư 1.

b) Các số tự nhiên có ba chữ số chia cho 9 dư 2 là: 101; 110; 119; 128; 237; …; 992.

Số các số tự nhiên có ba chữ số chia cho 9 dư 2 là: (992 – 101): 9 + 1 = 100.

Vậy có 100 số tự nhiên có ba chữ số chia cho 9 dư 2.

c) Ta có: 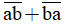 = 10a + b + 10b + a = 11a + 11b = 11.(a + b)

Vì 11 không chia hết cho 9 nên a + b chia hết cho 9.

Mà a, b là các chữ số nên a, b ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}

Các cặp số (a; b) là: (1; 8), (8; 1), (7; 2), (2; 7), (6; 3) (3; 6), (4; 5), (5; 4), (9; 9), (9; 0) thỏa mãn tổng chia hết cho 9.

Do đó 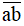 ∈ {18;81,72;27;63;36;45;54;99;90}.

Vậy có tất cả 10 số tự nhiên 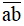 thỏa mãn bài toán.

Bài 84 trang 28 sách bài tập Toán lớp 6 Tập 1: Bạn Minh có chơi trò phi tiêu với ba cái tiêu. Lần thứ nhất, bạn Minh phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R thì được 12 điểm. Lần thứ hai, bạn Minh phi 2 tiêu vào vùng P và 1 tiêu vào cùng R thì được 18 điểm. Lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu. Hỏi số điểm lần thứ ba của bạn Minh có chia hết cho cả 3 và 5 không? Tại sao?

Lời giải:

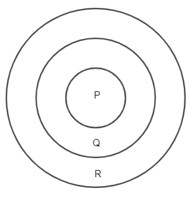
Tổng số điểm của bạn Minh ở hai lần đầu là: 12 + 18 (điểm).

Vì bạn Minh đã phi 2 tiêu vào vùng Q và 1 tiêu vào vùng R và phi 2 tiêu vào vùng P và 1 tiêu vào cùng R.

Như vậy sau lần thứ nhất và lần thứ hai bạn Minh phi được 2 tiêu vào vùng Q, 2 tiêu R và 2 tiêu vào vùng P. 

Suy ra tổng số điểm ba vùng là: 30:2 = 15 (điểm).

Do lần thứ ba, bạn Minh phi trúng mỗi vùng một tiêu nên số điểm lần thứ ba là 15 điểm.

Ta thấy 15 có chữ số tận cùng là 5 nên chia hết cho 5, 1 + 5 = 6 chia hết cho 3 nên 15 chia hết cho 3.

Vậy số điểm lần thứ ba của bạn Minh chia hết cho cả 3 và 5.

Bài 85 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho a là số tự nhiên có 2 004 chữ số và chia hết cho 9. Gọi b là tổng các chữ số của a; c là tổng các chữ số của b và d là tổng các chữ số của c. Tính d.

Lời giải:

Do a chia hết cho 9 nên tổng các chữ số của a chia hết cho 9. Mặt khác b là tổng các chữ số của a nên b chia hết cho 9.

Do b chia hết cho 9 nên tổng các chữ số của b chia hết cho 9. Mặt khác c là tổng các chữ số của b nên c chia hết cho 9.

Do c chia hết cho 9 nên tổng các chữ số của c chia hết cho 9. Mặt khác d là tổng các chữ số của c nên d chia hết cho 9.

Vì a là số tự nhiên có 2 004 chữ số, mỗi chữ số của a đều không vượt quá 9 nên b ≤ 2 004.9 = 18 036. Nghĩa là b có 5 chữ số.

Suy ra c < 9 + 9 + 9 + 9 = 9.5 = 45. Mặt khác c ≠ 0 và c chia hết cho 9 nên suy ra c ∈ {9; 18; 27; 36}.

Ta có d là tổng các chữ số của c nên d = 9 = 1 + 8 = 2 + 7 = 3 + 6.

Vậy d = 9.

Bài 86 trang 28 sách bài tập Toán lớp 6 Tập 1: Viết liên tiếp các số tự nhiên từ 10 đến 99 liền nhau ta được một số tự nhiên. Hỏi số đó chia hết cho 9 hay không? Vì sao?

Lời giải:

Gọi A là số được viết bởi 90 số từ 10 đến 99.

Tổng các chữ số hàng đơn vị của số này là: (0 + 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9). 9 = 405.

Tổng các chữ số hàng chục của số này là: (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9).10 = 450.

Vậy tổng các chữ số của số A là: 405 + 450 = 855.

Vì 8 + 5 + 5 =18 chia hết cho 9 nên 855 chia hết cho 9.

Vậy số A chia hết cho 9.

Bài 87 trang 28 sách bài tập Toán lớp 6 Tập 1: Không thực hiện phép tính, hãy giải thích tại sao phép nhân là sai: 7 654.658 = 5 136 332.

Lời giải:

Ta có: 7 + 6 + 5 + 4 = 22 chia cho 9 dư 4 nên 7 654 chia cho 9 dư 4.

Ta lại có: 6 + 5 + 8 = 19 chia cho 9 dư 1 nên 658 chia cho 9 dư 1.

Do đó 7 654.658 chia 9 dư 4.

Ta có: 5 + 1 + 3 + 6 + 3 + 3 + 2 = 23 chia cho 9 dư 3 nên 5 136 332 chia cho 9 dư 3.

Vậy phép tính 7 654.658 = 5 136 332 là sai.

Bài 88 trang 28 sách bài tập Toán lớp 6 Tập 1: Một công ty có 9 contenơ hàng với khối lượng hàng mỗi contenơ là: 193 tạ, 239 tạ, 277 tạ, 297 tạ, 316 tạ, 321 tạ, 329 tạ, 346 tạ, 355 tạ. Trong sáu tháng đầu năm công ty đó đã xuất khẩu 8 contenơ hàng, trong đó lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I. Contenơ hàng còn lại có khối lượng bằng bao nhiêu?

Lời giải:

Tổng khối lượng hàng của 9 contenơ hàng là:

193 + 239 + 277 + 297 + 316 + 321 + 329 + 346 + 355 = 2 673 (tạ).

Ta có: 2 + 6 + 7 + 3 = 18 chia hết cho 9 nên 2 673 chia hết cho 9.

Vì lượng hàng xuất khẩu của Quý II gấp 8 lần Quý I nên số lượng hàng trong 6 tháng đầu năm phải chia hết cho 9.

Do đó khối lượng hàng của contenơ còn lại phải chia hết cho 9.

Trong số 9 contenơ trên chỉ có contenơ có khối lượng 297 tạ là thỏa mãn chia hết cho 9.

Vậy contenơ hàng còn lại có khối lượng là 297 tạ.

Lý thuyết Dấu hiệu chia hết cho 3, cho 9

I. Dấu hiệu chia hết cho 3

Các số có tổng các chữ số chia hết cho 3 thì chia hết cho 3 và chỉ những số đó mới chia hết cho 3.

Ví dụ: 

+ Số 102 có tổng các chữ số là 1 + 0 + 2 = 3 chia hết cho 3 thì số 102 chia hết cho 3.

+ Số 321 có tổng các chữ số là 3 + 2 + 1 = 6 chia hết cho 3 thì số 321 chia hết cho 3.

II. Dấu hiệu chia hết cho 9

Các số có tổng các chữ số chia hết cho 9 thì chia hết cho 9 và chỉ những số đó mới chia hết cho 9.

Ví dụ: 

+ Số 792 có tổng các chữ số là 7 + 9 + 2 = 18 chia hết cho 9 thì số 792 chia hết cho 9.

+ Số 108 có tổng các chữ số là 1 + 0 + 8 = 9 chia hết cho 9 thì số 108 chia hết cho 9.