Với giải sách bài tập Toán 6 Bài 3: Phép cộng, phép trừ các số tự nhiên sách Cánh diều hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 3: Phép cộng, phép trừ các số tự nhiên

Bài 15 trang 10 sách bài tập Toán lớp 6 Tập 1: Cửa khẩu Hữu Nghị, Lạng Sơn, Bắc Ninh, Hà Nội theo thứ tự nằm trên Quốc lộ 1A. Số liệu của Tổng cục Đường bộ Việt Nam cho biết trên Quốc lộ 1A: Quãng đường Cửa khẩu Hữu Nghị - Lạng Sơn dài khoảng: 16km; Quãng đường Lạng Sơn – Bắc Ninh dài khoảng: 123 km; Quãng đường Bắc Ninh – Hà Nội dài khoảng 31km. Tính độ dài các quãng đường Hà Nội – Lạng Sơn, Bắc Ninh – Cửa khẩu Hữu Nghị trên Quốc lộ 1A.

Lời giải:

Độ dài quãng đường Hà Nội – Lạng Sơn trên Quốc lộ 1A bằng tổng quãng đường Lạng Sơn – Bắc Ninh và quãng đường Bắc Ninh – Hà Nội là: 123 + 31 = 154 (km).

Độ dài quãng đường Bắc Ninh – Cửa khẩu Hữu Nghị trên quốc lộ 1A bằng tổng quãng đường Cửa khẩu Hữu Nghị - Lạng sơn với quãng đường Lạng Sơn – Bắc Ninh là: 16 + 123 = 139 (km).

Bài 16 trang 11 sách bài tập Toán lớp 6 Tập 1: Tính một cách hợp lí:

a) 17 + 188 + 183;

b) 122 + 2 116 + 278 + 84;

c) 11 + 13 + 15 + 17 + 19.

Lời giải:

a) 17 + 188 + 183

= (17 + 183) + 188

= 200 + 188

= 388.

b) 122 + 2 116 + 278 + 84

= (122 + 278) + (2 116 + 84)

= 400 + 2 200

= 2 600.

c) 11 + 13 + 15 + 17 + 19

= (11 + 19) + (13 + 17) + 15

= 30 + 30 + 15

= 75.

Bài 17 trang 11 sách bài tập Toán lớp 6 Tập 1: Tính bằng cách tách một số hạng thành tổng của hai số hạng khác (theo mẫu):

Mẫu: 185 + 1 005 = 185 + (1 000 + 5) = (185 + 5) + 1 000 = 190 + 1 000 = 1 190.

a) 79 + 1 011;

b) 292 + 20 008 + 250;

c) 1 811 + 15 + 189 + 185.

Lời giải:

a) 79 + 1 011 = 79 + ( 1 010 + 1) = (79 + 1) + 1 010 = 80 + 1 010 = 1 090.

b) 292 + 20 008 + 250

= 292 + (20 000 + 8) + 250

= (292 + 8) + 20 000 + 250

= 300 + 20 000 + 250

= 20 550.

c) 1 811 + 15 + 189 + 185

= (1 800 + 11) + (15 + 185) + 189

= 1 800 + (11 + 189) + (15 + 185)

= 1 800 + 200 + 200

= 2 200.

Bài 18 trang 11 sách bài tập Toán lớp 6 Tập 1: Tìm chữ số x, biết:

a) 534 + 1 266 < 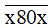 < 635 + 1 167;

b) 197 < 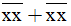 < 199.

Lời giải:

a) 534 + 1 266 < 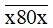 < 635 + 1 167;

Ta có: 534 + 1 266 = 1 800; 

635 + 1 167 = 1 802.

1 800 < 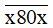 < 1 802.

Khi đó 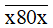 = 1 801.

Vậy x = 1.

b) 197 < 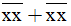 < 199

Suy ra 197 < 2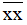 < 199

Do đó 2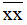 = 198

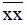 = 198:2 = 99.

Vậy x = 9.

Bài 19 trang 11 sách bài tập Toán lớp 6 Tập 1: Trong bảng dưới đây có ghi tổng diện tích và diện tích biển của các khu bảo tồn biển Nam Yết, Lý Sơn, Hải Vân – Sơn Chà:

a) Tổng diện tích khu bảo tồn biển Hải Vân – Sơn Chà ít hơn tổng diện tích khu bảo tồn Nam Yết bao nhiêu héc – ta?

b) Diện tích biển của khu bảo tồn biển Nam Yết nhiều hơn tổng diện tích biển của hai khu bảo tồn biển Lý Sơn và Hải Vân – Sơn Chà bao nhiêu hecta?

Lời giải:

a) Tổng diện tích khu bảo tồn biển Hải Vân – Sơn Chà ít hơn tổng diện tích khu bảo tồn Nam Yết là: 35 000 - 17 039 = 17 961 (hecta).

Vậy tổng diện tích khu bảo tồn biển Hải Vân – Sơn Chà ít hơn 17 961 hecta so với tổng diện tích khu bảo tồn Nam Yết.

b) Tổng diện tích biển khu bảo tồn biển Lý Sơn và Hải Vân – Sơn Chà là:

7 113 + 7 626 = 14 739 (hecta).

Diện tích biển của khu bảo tồn biển Nam Yết nhiều hơn tổng diện tích biển khu bảo tồn biển Lý Sơn và Hải Vân – Sơn Chà là: 20 000 – 14 739 = 5 261 (hecta).

Vậy tổng diện tích biển của khu bảo tồn biển Lý sơn nhiều hơn diện tích biển của khu bảo tồn biển Hải Vân – Sơn Chà là 5 261 hecta.

Bài 20 trang 11 sách bài tập Toán lớp 6 Tập 1: Nhà trường tổ chức hội chợ để gây quỹ ủng hộ “Trái tim cho em”. Lớp 6B vẽ một bức tranh và đem bán đấu giá với giá dự kiến là 370 000 đồng. Người thứ nhất trả cao hơn dự kiến là 40 000 đồng. Người thứ hai trả cao hơn người thứ nhất là 100 000 đồng và mua được bức tranh. Bức tranh được bán với giá bao nhiêu?

Lời giải:

Bức tranh được bán với giá là:

370 000 + 40 000 + 100 000 = 510 000 (đồng).

Vậy bức tranh được bán với giá 510 000 đồng.

Bài 21 trang 11 sách bài tập Toán lớp 6 Tập 1: Cho 2 021 số tự nhiên, trong đó có tổng của năm số bất kì đều là một số lẻ. Hỏi tổng của 2 021 số tự nhiên đó là số lẻ hay số chẵn.

Lời giải:

Vì tổng của năm số bất kì trong 2 021 số tự nhiên là một số lẻ nên trong 2 021 số này có ít nhất một số lẻ.

Gọi số lẻ đó là a, thì 2 020 số còn lại (bỏ đi số a) sẽ chia thành 404 nhóm, mỗi nhóm có 5 số.

Vì tổng của năm số bất kì là số lẻ nên tổng mỗi nhóm là lẻ. Do đó tổng của 404 nhóm sẽ là chẵn.

Suy ra tổng của 404 nhóm cộng với số lẻ a sẽ là một số lẻ.

Vậy tổng của 2 021 số tự nhiên đó là số lẻ.

Bài 22 trang 12 sách bài tập Toán lớp 6 Tập 1: Trên bảng có bộ ba số 2, 6, 9. Cứ sau mỗi phút, người ta thay đồng thời mỗi số trên bảng bằng tổng của hai số còn lại thì được một bộ ba số mới. Nếu cứ làm như vậy sau 30 phút thì hiệu của số lớn nhất và số bé nhất trong ba số trên bảng bằng bao nhiêu?

Lời giải:

Xét bài toán tổng quát:

Bộ ba số a, b, c (a < b < c).

Tổng của hai số bất kì trong ba số a, b, c là: a + b, b + c, c + a.

Vì a < b < c nên a + b < a + c < b + c.

Hiệu giữa hai tổng bất kì trong ba tổng trên bằng hiệu của hai trong ba số:

(b + c) – (a + b) = c – a;

(b + c) – (c +a) = b – a ;

(c + a) – (a + b) = c – b;

Vậy cứ làm theo yêu cầu đề bài sau 30 phút thì hiệu số lớn nhất và số bé nhất trong bộ ba số trên là: 9 – 2 = 7.

Lý thuyết Phép cộng, phép trừ các số tự nhiên

I. Phép cộng

1. Phép cộng hai số tự nhiên

a + b = c

        (số hạng) + (số hạng) = (tổng)

Ví dụ: 3 + 2 = 5; 10 + 24 = 34

2. Tính chất của phép cộng các số tự nhiên

+ Phép cộng các số tự nhiên có các tính chất: giao hoán, kết hợp, cộng với số 0. 

+ Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a + b + c có thể được tính theo một trong hai cách sau: a + b + c = (a + b) + c hoặc a + b + c = a + (b + c). 

Ví dụ: Tính: 65 + 97 + 35 

Lời giải:

   65 + 97 + 35 

= 65 + 35 + 97       (tính chất giao hoán)

= (65 + 35) + 97    (tính chất kết hợp)

= 100 + 97 

= 197 

II. Phép trừ

1. Phép trừ hai số tự nhiên

         a – b = c     (a  # b)

(số bị trừ) – (số trừ) = (hiệu)

Ví dụ: 12 – 7 = 5; 23 – 3 = 20 

2. Lưu ý

+ Nếu a – b = c thì a = b + c và b = a – c. 

+ Nếu a + b = c thì a = c – b và b = c – a.

Ví dụ: Tìm số tự nhiên x, biết: 125 + (237 – x) = 257. 

Lời giải:

125 + (237 – x) = 257 

           237 – x   = 257 – 125 

           237 – x   = 132

                     x    = 237 – 132 

                     x   = 105

Vậy x = 105. 

Lý thuyết Phép cộng, phép trừ các số tự nhiên

I. Phép cộng

1. Phép cộng hai số tự nhiên

a + b = c

        (số hạng) + (số hạng) = (tổng)

Ví dụ: 3 + 2 = 5; 10 + 24 = 34

2. Tính chất của phép cộng các số tự nhiên

+ Phép cộng các số tự nhiên có các tính chất: giao hoán, kết hợp, cộng với số 0. 

+ Chú ý: Do tính chất kết hợp nên giá trị của biểu thức a + b + c có thể được tính theo một trong hai cách sau: a + b + c = (a + b) + c hoặc a + b + c = a + (b + c). 

Ví dụ: Tính: 65 + 97 + 35 

Lời giải:

   65 + 97 + 35 

= 65 + 35 + 97       (tính chất giao hoán)

= (65 + 35) + 97    (tính chất kết hợp)

= 100 + 97 

= 197 

II. Phép trừ

1. Phép trừ hai số tự nhiên

         a – b = c     (a  # b)

(số bị trừ) – (số trừ) = (hiệu)

Ví dụ: 12 – 7 = 5; 23 – 3 = 20 

2. Lưu ý

+ Nếu a – b = c thì a = b + c và b = a – c. 

+ Nếu a + b = c thì a = c – b và b = c – a.

Ví dụ: Tìm số tự nhiên x, biết: 125 + (237 – x) = 257. 

Lời giải:

125 + (237 – x) = 257 

           237 – x   = 257 – 125 

           237 – x   = 132

                     x    = 237 – 132 

                     x   = 105

Vậy x = 105.