Với giải sách bài tập Toán 6 Bài 32: Điểm và đường thẳng sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 32: Điểm và đường thẳng
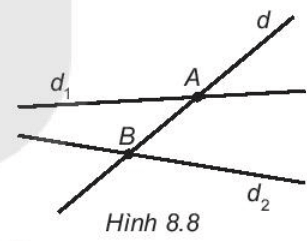
Bài 8.1 trang 42 sách bài tập Toán lớp 6 Tập 2: Quan sát Hình 8.8
Dùng kí hiệu để trả lời câu hỏi: điểm A thuộc đường thẳng nào và không thuộc đường thẳng nào?
Lời giải:
Trên Hình 8.8:
- Điểm A nằm trên đường thẳng d và d1 hay điểm A thuộc đường thẳng d và d1. Ký hiệu: A ∈ d, A ∈ d1.
- Điểm A không nằm trên đường thẳng d2 hay điểm A thuộc đường thẳng d2. Ký hiệu: A ∉ d2.
Vậy A ∈ d, A ∈ d1, A ∉ d2.
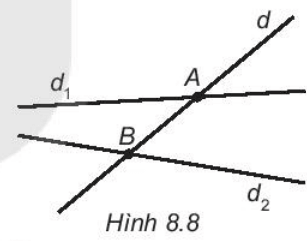
Bài 8.2 trang 42 sách bài tập Toán lớp 6 Tập 2: Quan sát Hình 8.8
Hãy kể một tên khác của đường thẳng AB.
Lời giải:
Cách gọi tên đường thẳng:
Cách 1: Gọi theo tên đường thẳng, được đặt tên bằng các chữ cái thường như: a, b, c, d,…
Cách 2: Gọi tên theo hai điểm bất kỳ nằm trên đường thẳng (hai điểm này không trùng nhau).
Vậy một tên khác của đường thẳng AB trên Hình 8.8 là đường thẳng d.
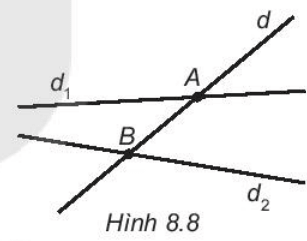
Bài 8.3 trang 42 sách bài tập Toán lớp 6 Tập 2: Quan sát Hình 8.8
Đường thẳng d cắt những đường thẳng nào? Với mỗi trường hợp, hãy nêu tên của giao điểm.
Lời giải:
Đường thẳng d cắt những đường thẳng d1 và d2.
- Giao điểm của hai đường thẳng d và d1 là điểm A;
- Giao điểm của hai đường thẳng d và d2 là điểm B.
Bài 8.4 trang 42 sách bài tập Toán lớp 6 Tập 2: Quan sát Hình 8.8
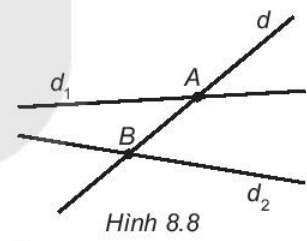
Hai đường thẳng d1 và d2 có song song với nhau không, tại sao?
Lời giải:
Kéo dài d1 và d2 thì ta thấy chúng cắt nhau.
Vậy hai đường thẳng d1 và d2 không song song
Bài 8.5 trang 42 sách bài tập Toán lớp 6 Tập 2: Vẽ hình thể hiện các quan hệ:
Đường thẳng d và hai điểm A ∈ d và B ∉ d.
Lời giải:
Lời giải:
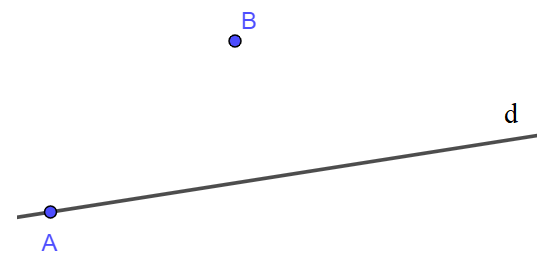
Cách vẽ:
- Vẽ đường thẳng d.
- Lấy điểm A bất kì nằm trên d.
- Lấy điểm B bất kì không nằm trên d.
Ta có hình vẽ:
Bài 8.6 trang 42 sách bài tập Toán lớp 6 Tập 2: Vẽ hình thể hiện các quan hệ:
Hai đường thẳng a, b và hai điểm M, N sao cho M ∈ a, M ∈ b, N ∈ b.
Lời giải:
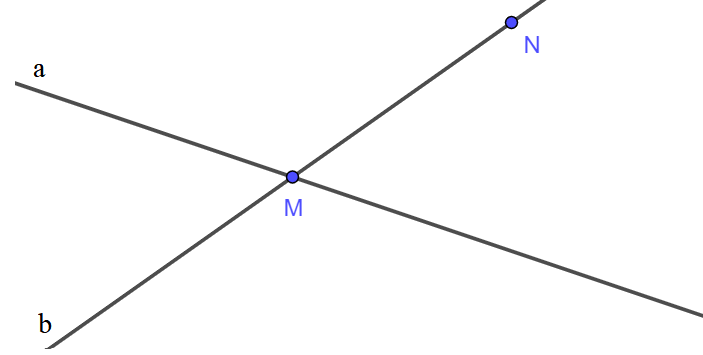
Cách vẽ:
- Vẽ 2 đường thẳng a, b cắt nhau.
- Lấy giao điểm của hai đường thẳng a và b là điểm M.
- Lấy điểm N nằm trên đường thẳng b.
Ta có hình vẽ:
Lời giải:
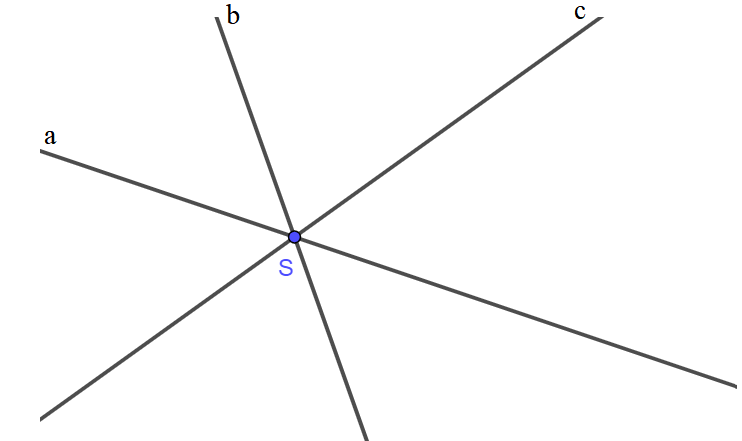
Cách vẽ:
- Vẽ hai đường thẳng a và b cắt nhau tại S.
- Vẽ đường thẳng c đi qua điểm S. Ta được ba đường thẳng a, b, c cùng đi qua điểm S (như hình vẽ).
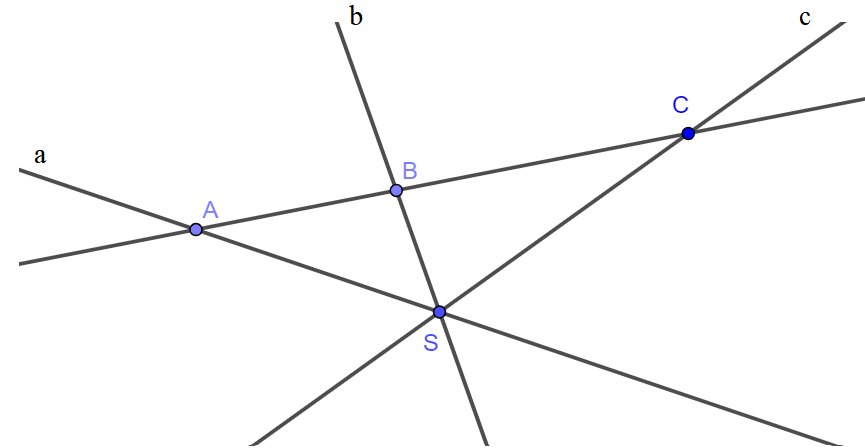
- Lấy điểm A nằm trên đường thẳng a.
- Lấy điểm B nằm trên đường thẳng b.
- Vẽ đường thẳng đi qua hai điểm A và B cắt đường thẳng c tại điểm C.
Ta được ba điểm A ∈ a, B ∈ b, C ∈ c thẳng hàng.
Ta có hình vẽ:
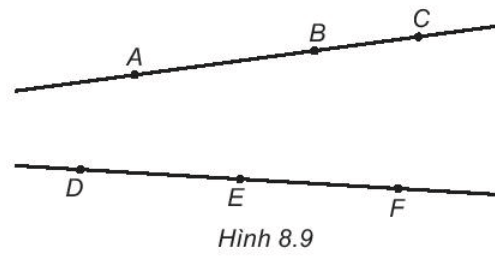
Bài 8.8 trang 42 sách bài tập Toán lớp 6 Tập 2: Vẽ Hình 8.9 vào vở.
Lời giải:
Vẽ các đường thẳng AE, BD, BF, EC, AF và DC.
Lời giải:
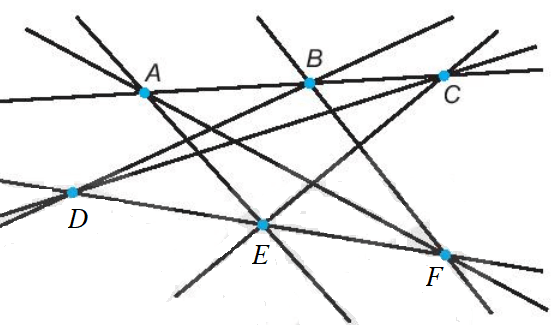
Nối các điểm: A với E, B với D, B với F, E với C, A với F, D với C.
Ta được các đường thẳng AE, BD, BF, EC, AF và DC.
Ta có hình vẽ:
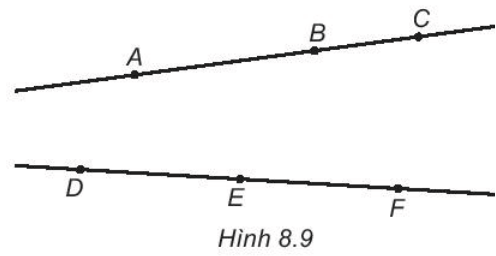
Bài 8.9 trang 43 sách bài tập Toán lớp 6 Tập 2: Vẽ Hình 8.9 vào vở.
Xác định các giao điểm I của AE và BD, J của BF và EC, K của AF và DC.
Lời giải:
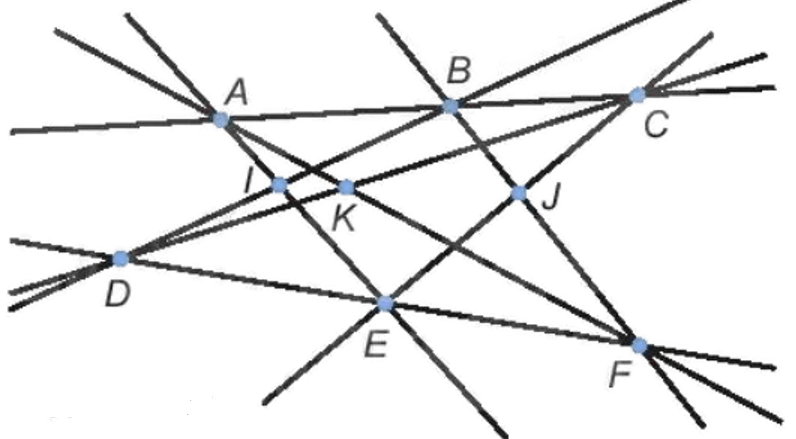
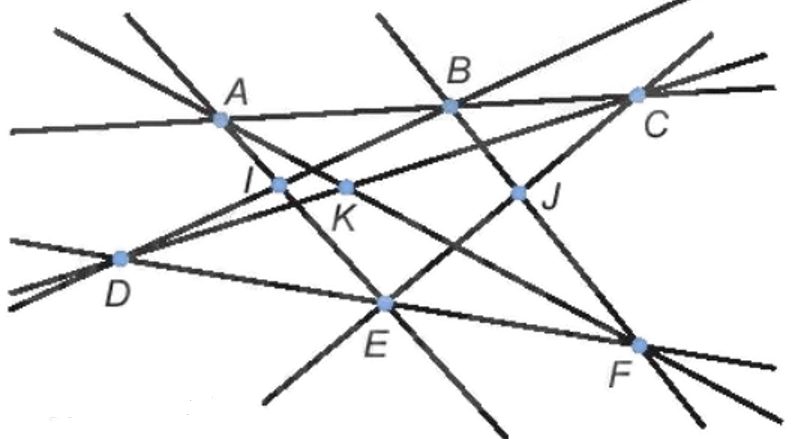
- Nối A với E, B với D; ta được đoạn thẳng AE và BD. Hai đoạn thẳng này cắt nhau tại điểm I.
- Nối B với F, E với C; ta được đoạn thẳng BF và EC. Hai đoạn thẳng này cắt nhau tại điểm J.
- Nối A với F, D với C; ta được đoạn thẳng AF và DC. Hai đoạn thẳng này cắt nhau tại điểm K.
Ta có hình vẽ:
Lời giải:
Cách kiểm tra:
- Đặt thước sao cho mép thước dọc theo đường thẳng đi qua hai trong ba điểm I, J, K. Chẳng hạn: Đặt thước sao cho mép thước dọc theo đường thẳng đi qua hai điểm I và K (như hình vẽ dưới).
- Kiểm tra xem đường thẳng có đi qua điểm J hay không.
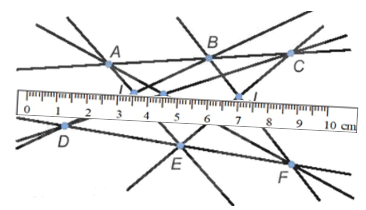
Nhận thấy: đường thẳng đi qua hai điểm I và K cũng đi qua đểm J.
Do đó ba điểm I, J, K thẳng hàng.
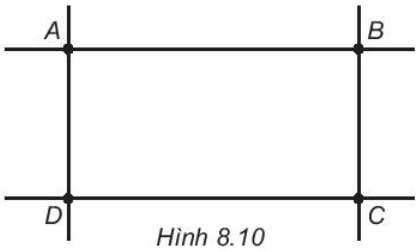
Bài 8.11 trang 43 sách bài tập Toán lớp 6 Tập 2: Cho Hình 8.10.
a) Kiểm tra xem hai đường thẳng AB và CD có song song với nhau không. Làm tương tự đối với hai đường thẳng AD và BC.
b) Tìm điểm I sao cho ba điểm A, I, C thẳng hàng, ba điểm B, I, D cũng thẳng hàng.
Lời giải:
a) Kéo dài AB và CD về hai phía và kiểm tra. Ta thấy AB và CD không có điểm chung.
Do đó, hai đường thẳng AB và CD song song với nhau.
Kéo dài AD và BC về hai phía và kiểm tra. Ta thấy AD và BC không có điểm chung.
Do đó, hai đường thẳng AD và BC song song với nhau.
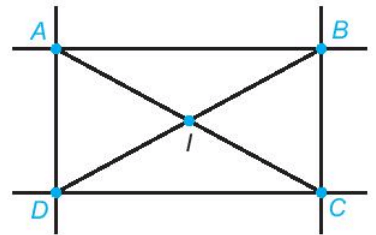
b) Nối A với C, B với D. Hai đường chéo AC và BD cắt nhau tại I.
Khi đó, ba điểm A, I, C thẳng hàng, ba điểm B, I, D cũng thẳng hàng.
Ta có hình vẽ:
Lời giải:
Cách vẽ ba đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm:
- Vẽ hai đường thẳng cắt nhau. Đặt tên hai đường thẳng đó là a và b. Hai đường thẳng này cắt nhau tại điểm A.
- Vẽ đường thẳng c không đi qua điểm A cắt đường thẳng a và b lần lượt tại hai điểm B và C.
Ta có hình vẽ:
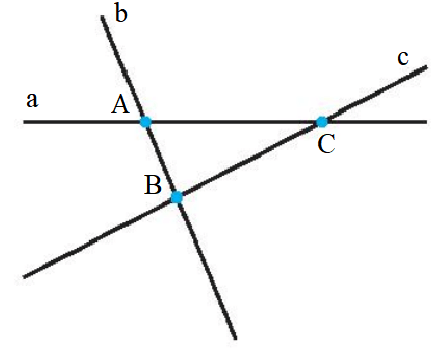
Ta thấy ba đường thẳng a, b, c đôi một cắt nhau nhưng không cùng đi qua một điểm và có ba giao điểm được tạo thành là A, B, C.
Vậy ba đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì có ba giao điểm.
Nhận xét: Có 3 đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì có 3 . (3 – 1) : 2 = 3 (giao điểm).
Lời giải:
Cách vẽ:
- Vẽ hai đường thẳng cắt nhau. Đặt tên hai đường thẳng đó là đường thẳng a và b, chúng cắt nhau tại điểm A.
- Vẽ đường thẳng c không đi qua điểm A và cắt hai đường thẳng a và b lần lượt tại điểm C và B.
- Vẽ đường thẳng d không đi qua một trong ba điểm A, B, C và cắt ba đường thẳng a, b, c lần lượt tại ba điểm D, E, G.
Ta có hình vẽ:
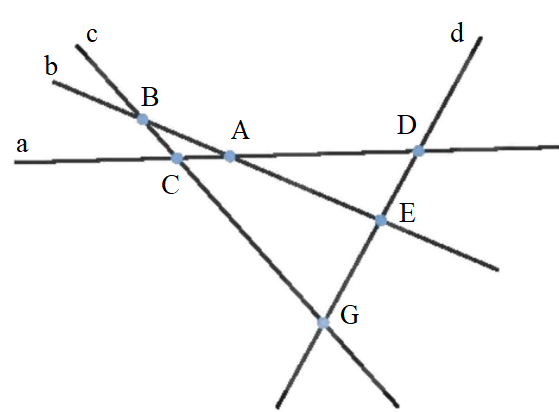
Ta thấy từ bốn đường thẳng a, b, c, d đôi một cắt nhau nhưng không cùng đi qua một điểm thì tạo ra 6 giao điểm A, B, C, D, E, G.
Vậy từ bốn đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì tạo ra 6 giao điểm.
Nhận xét: Có 4 đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì có 4 . (4 – 1) : 2 = 6 (giao điểm).
Lời giải:
Cách vẽ:
- Vẽ hai đường thẳng cắt nhau. Đặt tên hai đường thẳng đó là đường thẳng a và b, chúng cắt nhau tại điểm A.
- Vẽ đường thẳng c không đi qua điểm A và cắt hai đường thẳng a và b lần lượt tại điểm C và B.
- Vẽ đường thẳng d không đi qua một trong ba điểm A, B, C và cắt ba đường thẳng a, b, c lần lượt tại ba điểm D, E, G.
- Vẽ đường thẳng e không đi qua một trong 6 điểm A, B, C, D, E, G và cắt bốn đường thẳng a, b, c, d lần lượt tại bốn điểm H, I, M, K.
Ta có hình vẽ:
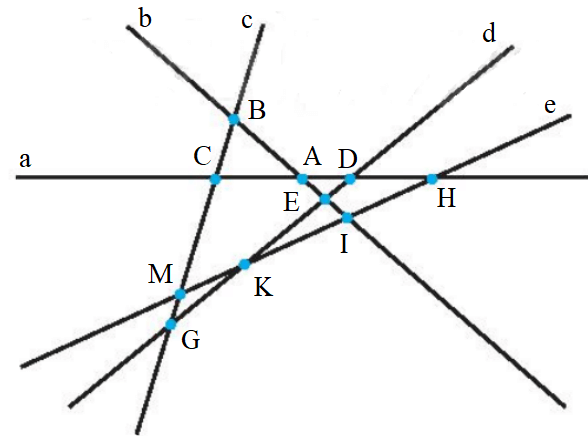
Ta thấy từ năm đường thẳng a, b, c, d, e đôi một cắt nhau nhưng không cùng đi qua một điểm thì tạo ra 10 giao điểm A, B, C, D, E, G, H, I, M, K.
Vậy từ năm đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì tạo ra 10 giao điểm.
Nhận xét: Có 5 đường thẳng đôi một cắt nhau nhưng không cùng đi qua một điểm thì có 5 . (5 – 1) : 2 = 10 (giao điểm).
Lời giải:
Bốn điểm M, N, A, B cùng nằm trên một đường thẳng nên điểm M và điểm N đều nằm trên đường thẳng đi qua hai điểm A và B cho trước.
Mặt khác, điểm M thuộc đường thẳng m và điểm N thuộc đường thẳng n.
Khi đó, điểm M vừa thuộc đường thẳng AB vừa thuộc đường thẳng m, điểm N vừa thuộc đường thẳng AB vừa thuộc đường thẳng n.
Do đó, điểm M là giao điểm của hai đường thẳng AB và m, điểm N là giao điểm của hai đường thẳng AB và n.
Nếu đường thẳng AB cắt hai đường thẳng m và n thì các giao điểm ấy chính là hai điểm M và N cần tìm (như hình vẽ).
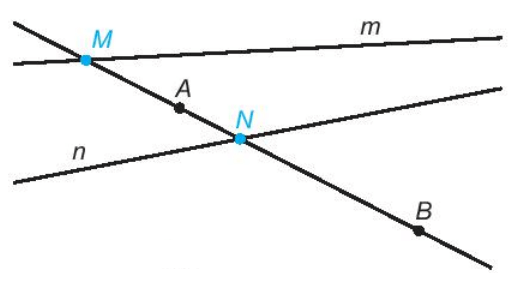
Trái lại, nếu đường thẳng AB song song với m thì không tìm được điểm M.
Nếu đường thẳng AB song song với n thì không tìm được điểm N.
Vậy không tìm được các điểm M và N khi đường thẳng AB song song với một trong hai đường thẳng m và n.
Lý thuyết Điểm và đường thẳng
1. Điểm thuộc, không thuộc đường thẳng
a) Điểm, đường thẳng
- Dùng bút chấm 1 chấm nhỏ cho ta một hình ảnh về điểm.
- Dùng bút chì và thước thẳng, vẽ được một vạch thẳng cho ta hình ảnh về một đường thẳng.
- Ta thường dùng chữ cái in hoa để đặt tên điểm và dùng chữ cái thường để đặt tên đường thẳng.
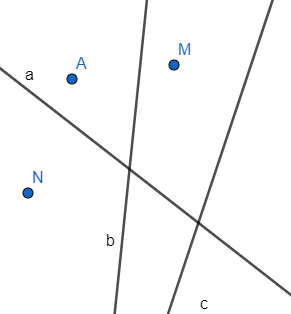
Ví dụ 1:
- Điểm M; điểm N; điểm A; …
- Đường thẳng a; đường thẳng b; đường thẳng c; …
b) Điểm thuộc đường thẳng, điểm không thuộc đường thẳng
- Điểm thuộc đường thẳng nếu điểm đó nằm trên đường thẳng đó hay đường thẳng đó đi qua điểm đó.
- Điểm không thuộc đường thẳng nếu điểm đó không nằm trên đường thẳng hay đường thẳng đó không đi qua điểm đó.
- Ta dùng kí hiệu ∈ thể hiện điểm thuộc đường thẳng và ∉ để thể hiện điểm không thuộc đườn thẳng.
Ví dụ 2:
Quan sát hình vẽ ta có:
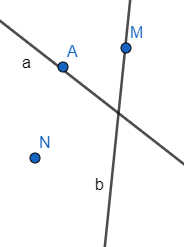
- Điểm A nằm trên đường thẳng a nên A ∈ a.
- Điểm M nằm trên đường thẳng b nên M ∈ b.
- Điểm A không nằm trên đường thẳng b nên A ∉ b.
- Điểm M không nằm trên đường thẳng a nên M ∉ a.
- Điểm N không nằm trên đường thẳng b nên N ∉ b.
- Điểm N không nằm trên đường thẳng a nên N ∉ a.
c) Đường thẳng đi qua hai điểm phân biệt
- Có một đường thẳng và chỉ một đường thẳng đi qua hai điểm phân biệt
Ví dụ 3: Qua hai điểm M, N ta chỉ vẽ được duy nhất một đường thẳng đi qua hai điểm M, N.
Chú ý: Để nhấn mạnh hai phía của đường thẳng, người ta còn dùng hai chữ cái thường để đặt tên, chẳng hạn đường thẳng xy (hoặc yx)
2. Ba điểm thẳng hàng
- Ba điểm thẳng hàng là ba điểm thuộc cùng một đường thẳng.
Ví dụ 4: Cho hai hình vẽ
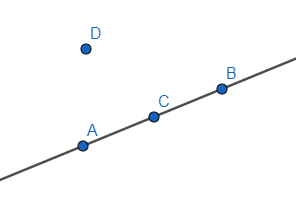
- Quan sát hình vẽ ta thấy
Ba điểm A, B, C thẳng hàng vì nó thuộc cùng một đường thẳng.
Ba điểm A, D, C không thẳng hàng vì nó không thuộc cùng một đường thẳng.
3. Hai đường thẳng song song, cắt nhau, trùng nhau.
- Hai đường thẳng song song là hai đường thẳng không có điểm chung. Kí hiệu song song là //.
- Hai đường thẳng cắt nhau là hai đường thẳng có một điểm chung.
- Hai đường thẳng trùng nhau là hai đường thẳng có vô số điểm chung.
|
|
|
|
|
a và b song song với nhau kí hiệu: a // b |
a và b cắt nhau tại điểm E |
Đường thẳng AB và đường thẳng BC trùng nhau. |
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
