Với giải sách bài tập Toán 6 Bài 21: Hình có trục đối xứng sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Bài 21: Hình có trục đối xứng
Lời giải:
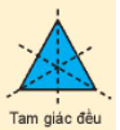
+) Hình tam giác đều có 3 trục đối xứng là:
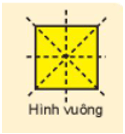
+) Hình vuông có 4 trục đối xứng là:
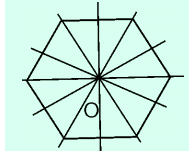
+) Hình lục giác đều có 6 trục đối xứng là:
+) Hình tròn có vô số trục đối xứng là: đường thẳng đi qua tâm
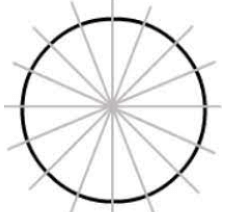
Lời giải:
Vẽ các trục đối xứng (nếu có) của các hình:
a) Chữ cái và chữ số có đúng một trục đối xứng;
b) Chữ cái và chữ số có hai trục đối xứng.
Lời giải:
a) Các chữ cái và chữ số có đúng một trục đối xứng là: A, B, M, Y, 3.
b) Các chữ cái và chữ số có hai trục đối xứng là: H, X, 0, 8
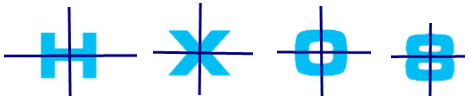
Lời giải:
Biểu tượng có trục đối xứng là: biểu tượng Hòa bình, biểu tượng Hội Chữ thập đỏ.
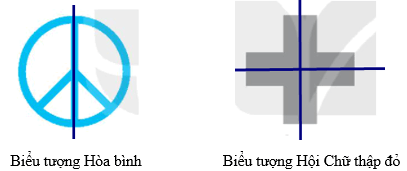
Lời giải:
Các trục đối xứng (nếu có) của các hình như sau:
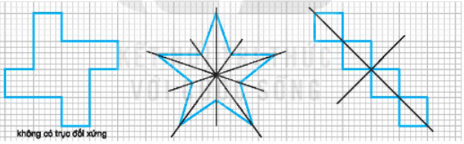
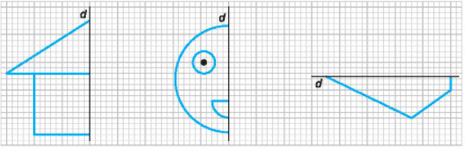
Lời giải:
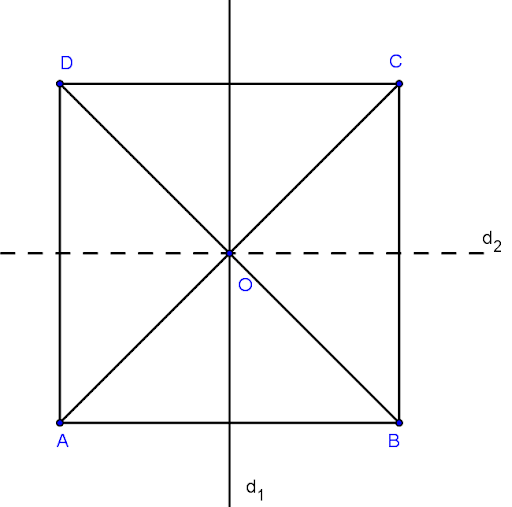
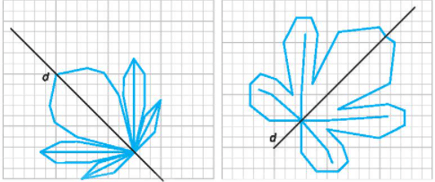
Các hình nhận d là trục đối xứng là:
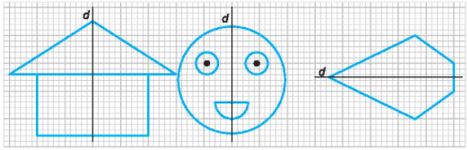
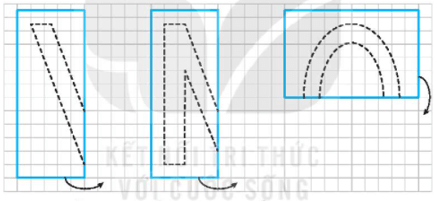
Lời giải:
Bạn Tròn nhận được lần lượt các chữ cái: V, M, O
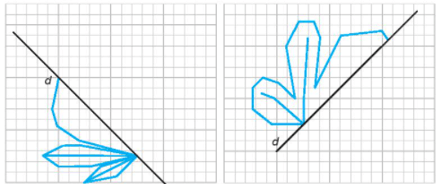
Lời giải:
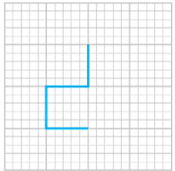
Em hãy vẽ thêm vào hình đó:
a) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng một trục đối xứng;
b) Một đường gấp khúc có độ dài bằng 4 đơn vị để được một hình có đúng hai trục đối xứng;
c) Một đường gấp khúc có độ dài bằng 8 đơn vị để được một hình có đúng bốn trục đối xứng.
Lời giải:
a) Hình vẽ thêm có đúng một trục đối xứng là:
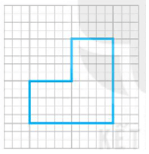
Với trục đối xứng như sau:
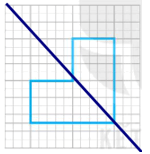
b) Hình vẽ thêm có đúng hai trục đối xứng là:
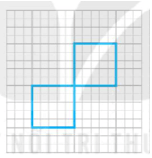
Với các trục đối xứng như sau:
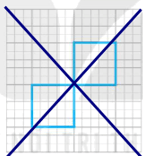
c) Hình vẽ thêm có đúng bốn trục đối xứng là:
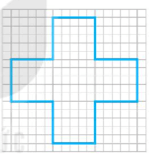
Với các trục đối xứng như sau:
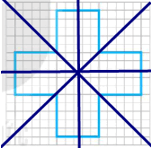
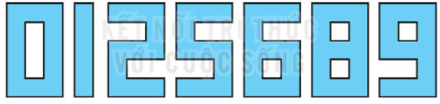
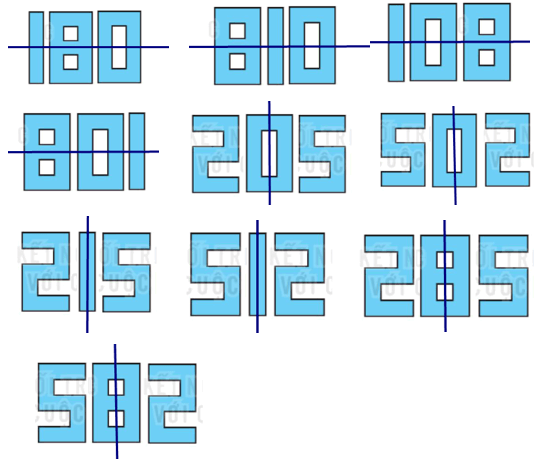
Em có thể ghép được tất cả bao nhiêu “số” như vậy?
Lời giải:
Ta có 10 số có trục đối xứng là: 180; 810; 108; 801; 205; 502; 215; 512; 285; 582.
Lý thuyết Hình có trục đối xứng
1. Hình có trục đối xứng trong thực tế
Các hình có một đường thẳng d chia hình đó thành hai phần mà nếu “gấp” hình theo đường thẳng d thì hai phần đó “chồng khít” lên nhau. Những hình như thế được gọi là hình có trục đối xứng và đường thẳng d là trục đối xứng của nó.
Ví dụ 1. Những hình ảnh có trục đối xứng trong thực tế
2. Trục đối xứng của một số hình phẳng
Mỗi đường thẳng đi qua tâm là một trục đối xứng của hình tròn. Do đó hình tròn có vô số trục đối xứng.
Mỗi đường chéo là một trục đối xứng của hình thoi.
Mỗi đường thẳng đi qua trung điểm hai cạnh đối diện là một trục đối xứng của hình chữ nhật.
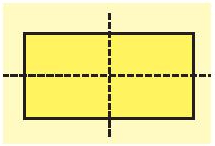
Hình vuông có 4 trục đối xứng bao gồm: Hai đường thẳng đi qua trung điểm hai cạnh đối điện và hai đường chéo.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
