Với giải sách bài tập Toán 6 Bài 18: Hình tam giác đều. hình vuông. Hình lục giác đều sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 18: Hình tam giác đều. hình vuông. Hình lục giác đều

Bài 4.1 trang 64 sách bài tập Toán lớp 6 Tập 1: Quan sát Hình 4. 4 và cho biết: Hình nào là hình tam giác đều, hình nào là hình vuông, hình nào là hình lục giác đều?

Lời giải:

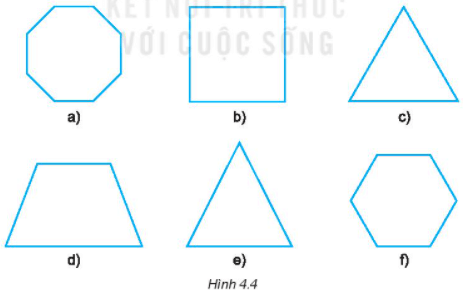
Quan sát hình 4.4, ta thấy:

+) Hình tam giác đều là: hình c

+) Hình vuông là: hình b

+) Hình lục giác đều là: hình f.

Bài 4.2 trang 65 sách bài tập Toán lớp 6 Tập 1: Vẽ tam giác đều MNP có cạnh MN = 4cm.

Lời giải:

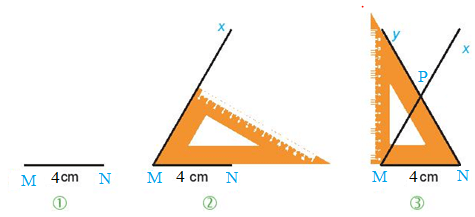
Vẽ tam giác đều MNP có cạnh 4cm theo hướng dẫn sau:

Bước 1. Vẽ đoạn thẳng MN = 4 cm.

Bước 2. Dùng ê ke có góc   vẽ góc NMx bằng  .

Bước 3. Vẽ góc MNy bằng  . Ta thấy Mx và Ny cắt nhau tại P, ta được tam giác đều MNP.

Bài 4.3 trang 65 sách bài tập Toán lớp 6 Tập 1: Vẽ hình vuông DEFQ có cạnh DE = 5 cm. Vẽ hai đường chéo DF và EQ.

Hãy kiểm tra xem DF và EQ có vuông góc với nhau không?

Lời giải:

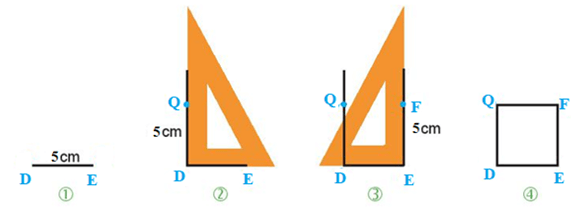
Vẽ hình vuông DEFQ có cạnh DE = 5cm 

Bước 1. Vẽ đoạn thẳng DE = 5 cm.

Bước 2. Vẽ đường thẳng vuông góc với DE tại D. Xác định điểm Q trên đường thẳng đó sao cho DQ = 5 cm.

Bước 3. Vẽ đường thẳng vuông góc với DE tại E. Xác định điểm F trên đường thẳng đó sao cho EF = 5 cm.

Bước 4. Nối F với Q ta được hình vuông DEFQ.

Vẽ hai đường chéo DF và QE ta được:

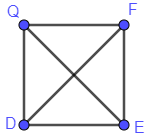
+) Khi sử dụng ê – ke ta thấy hai đường chéo DF và QE vuông góc với nhau.

Bài 4.4 trang 65 sách bài tập Toán lớp 6 Tập 1: Quan sát Hình 4.5.

a) Gọi tên các đường chéo phụ của hình lục giác đều MNPQRS;

b) Hãy đo độ dài các cạnh và cho biết các tam giác MPR và tam giác NQS trong Hình 4.5 có là tam giác đều không?

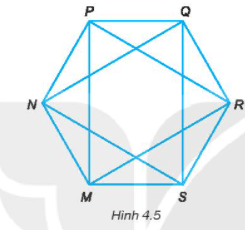
Lời giải:

Trong hình 4. 5, ta có:

a) Các đường chéo phụ của hình lục giác đều MNPQRS là: NQ; QS; SN; MP; PR; MR.

b) Sử dụng thước thẳng đo hoặc compa ta thấy:

+) MP = PR = MR. Do đó tam giác MPR là tam giác đều.

+) NQ = QS = NS. Do đó tam giác NQS là tam giác đều.

Bài 4.5 trang 65 sách bài tập Toán lớp 6 Tập 1: Quan sát hình 4.6.

a) Dùng compa kiểm tra xem hình ABC có là hình tam giác đều không.

b) Dùng compa và ê ke (hoặc thước đo góc) để kiểm tra hình MNPQ có là hình vuông không?

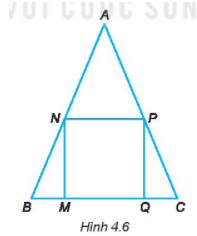
Lời giải:

a) Dùng compa đặt tâm ở điểm A và đầu chì ở điểm còn lại B, sau đó giữ nguyên khoảng cách compa, di chuyển compa đến đầu tâm đến điểm B, điểm còn lại nằm trên đoạn thẳng BC, ta thấy đầu chì không ở điểm C. Do đó AB và BC là hai đoạn thẳng không bằng nhau.

Vậy tam giác ABC không là tam giác đều.

b) 

+) Dùng compa để kiểm tra các đoạn thẳng MN, MQ, PQ, NP ta thấy 

MN = MQ = PQ = NP. Do đó 4 cạnh của hình MNPQ bằng nhau.

+) Dùng ê ke để kiểm tra các góc của hình MNPQ ta thấy:

MN vuông góc với MQ và NP hay góc NMQ và góc MNP đều bằng 90^o  

PQ vuông góc với QM và NP hay góc MQP và góc NPQ đều bằng 90^o  

Suy ra: các góc NMQ, góc MNP, góc MQP, góc NPQ đều bằng 90^o  

Do đó hình MNPQ có 4 góc vuông ở các đỉnh

Vậy MNPQ là hình vuông.

Bài 4.6 trang 66 sách bài tập Toán lớp 6 Tập 1: Em hãy cắt 6 hình tam giác đều có cạnh là 5 cm và ghép lại thành một hình lục giác đều (H.4.7). Hãy tính độ dài đường chéo chính của hình lục giác đều vừa ghép được.

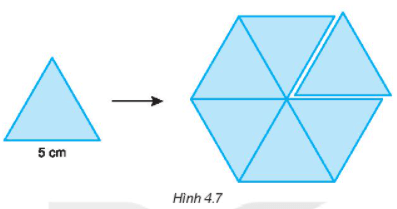
Lời giải:

Ở hình 4.7, ta thấy độ dài đường chéo chính của hình lục giác đều bằng hai lần cạnh của tam giác đều

Do đó độ dài đường chéo chính của hình lục giác đều vừa ghép được là:

5. 2 = 10 (cm)

Vậy độ độ dài đường chéo chính của hình lục giác đều vừa ghép được là 10cm.

Bài 4.7 trang 66 sách bài tập Toán lớp 6 Tập 1: Quan sát Hình 4.8.

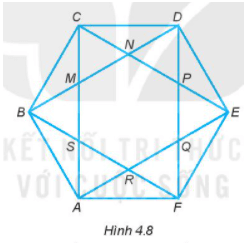
a) Hãy kiểm tra xem có mấy hình lục giác đều. Đó là những hình nào?

b) Có tất cả bao nhiêu tam giác đều?

Lời giải:

a) Dùng thước thẳng kiểm tra các cạnh ta thấy: 

+) AB = BC = CD = DE = EF = FA nên ta có ABCDEF là hình lục giác đều

+) MN = NP = PQ = QR = RS = SM nên ta có MNPQRS là hình lục giác đều.

Vậy có 2 hình lục giác đều là ABCDEF và MNPQRS.

b) Dùng thước thẳng hoặc compa để kiểm tra, ta thấy MN = CN = CM nên tam giác CMN là tam giác đều

Tương tự kiểm tra với các tam giác khác, ta thấy các tam giác đều là: ACE, BDF, ASR, BMS, DNP, EPQ, FQR.

Vậy ta có 8 giác đều là tam giác ACE, BDF, ASR, BMS, DNP, EPQ, FQR, CMN.

Lý thuyết Hình tam giác đều, hình vuông, hình lục giác đều

1. Hình tam giác đều

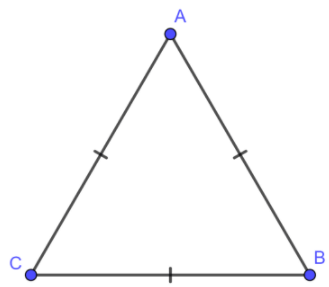
Trong tam giác đều:

- Ba cạnh bằng nhau.

- Ba góc bằng nhau và bằng 60⁰C.

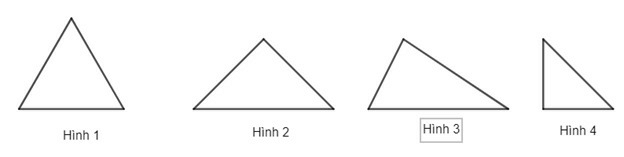
Ví dụ 1. Trong các hình dưới đây, hình nào là tam giác đều:

Lời giải

Sử dụng thước thẳng đo lần lượt các cạnh của từng hình, ta nhận thấy:

Hình 1 có độ dài các cạnh bằng nhau. Do đó HÌnh 1 là tam giác đều.

2. Hình vuông

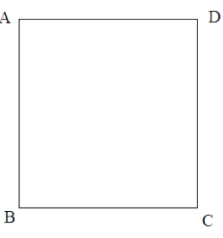
Trong hình vuông:

- Bốn cạnh bằng nhau.

- Bốn góc bằng nhau và bằng 90⁰.

- Hai đường chéo bằng nhau.

Ví dụ 2. Vẽ hình vuông ABCD có cạnh bằng 5cm.

Lời giải

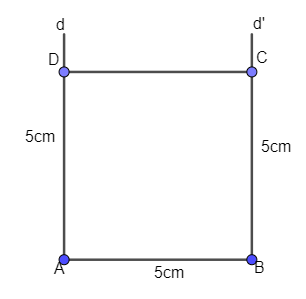
Bước 1. Vẽ đoạn thẳng AB = 5cm;

Bước 2. Qua A dựng đường thẳng d vuông góc với AB, qua B dựng đường thẳng d’ vuông góc với AB.

Bước 3. Trên đường thẳng d lấy điểm D sao cho AD = 5cm, trên d’ lấy điểm C sao cho BC = 5cm.

Bước 4. Nối D với C ta được hình vuông ABCD.

3. Hình lục giác đều

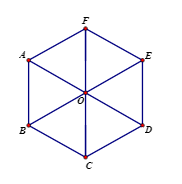
Hình lục giác đều có:

- Sáu cạnh bằng nhau.

- Sáu góc bằng nhau, mỗi góc bằng 120⁰.

- Ba đường chéo chính bằng nhau.

Ví dụ 3. Hãy quan sát hình vẽ:

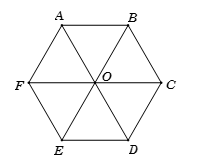
a) Hãy kể tên các đường chéo chính của hình lục giác đều ABCDEF.

b) Hãy so sánh độ dài các đường chéo chính với nhau.

Lời giải

a) Các đường chéo chính của hình lục giác đều ABCDEF là: AD, BE, CF.

b) Sau khi đo độ dài ta thấy AD = BE = CF = 2,1 cm.