Với giải sách bài tập Toán 6 Ôn tập chương 1 trang 28, 29 sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:
Giải SBT Toán lớp 6 Ôn tập chương 1 trang 28, 29
Câu hỏi (Trắc Nghiệm)
Bài 1 trang 28 sách bài tập Toán lớp 6 Tập 1: Tập hợp các chữ cái trong cụm từ LÀO CAI là:
(A) {LÀO; CAI};
(B) {L; À; O; C; A; I}
(C) {L; A; O; C; A; I}
(D) {L; A; O; C; I}
Lời giải:
Các chữ cái trong từ “LÀO CAI” gồm L, A, O, C, A, I.
Trong các chữ cái trên, chữ A được xuất hiện 2 lần nhưng ta chỉ viết mỗi chữ một lần, ta có tập hợp các chữ cái {L; A; O; C; I}
Đáp án cần chọn là: D
Bài 2 trang 28 sách bài tập Toán lớp 6 Tập 1: Trong các chữ số của số 19 254;
(A) Giá trị của chữ số 2 bằng nửa giá trị của chữ số 4;
(B) Giá trị của chữ số 2 bằng 5 lần giá trị của chữ số 4;
(C) Giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4;
(D) Giá trị của chữ số 2 bằng 500 lần giá trị của chữ số 4;
Lời giải:
+) Ta thấy số 19 254 có chữ số 2 đứng ở hàng trăm nên có giá trị là 2. 100 = 200
+) Ta thấy số 19 254 có chữ số 4 đứng ở hàng đơn vị nên có giá trị là 4. 1 = 4
Ta có: 200: 4 = 50
Do đó giá trị của chữ số 2 bằng 50 lần giá trị của chữ số 4
Đáp án cần chọn là: C
(A) a = 24 000 + 50 + 3;
(B) a = 20 000 + 4 000 + 53
(C) a = 20 000 + 4 000 + 50 + 3
(D) a = 20 000 + 4 050 + 3
Lời giải:
Số a = 24 053 có:
+) Chữ số 2 nằm ở hàng chục nghìn và có giá trị bằng 2 x 10 000 = 20 000
+) Chữ số 4 nằm ở hàng nghìn và có giá trị bằng 4 x 1 000 = 4 000
+) Chữ số 0 nằm ở hàng trăm và có giá trị bằng 0 x 100 = 0
+) Chữ số 5 nằm ở hàng chục và có giá trị bằng 5 x 10 = 50
+) Chữ số 3 nằm ở hàng đơn vị và có giá trị bằng 3 x 1 = 3
Vậy a = 20 000 + 4 000 + 50 + 3
Đáp án cần chọn là: C
Bài 4 trang 28 sách bài tập Toán lớp 6 Tập 1: Cho m ∈ N*. Ba số tự nhiên liên tiếp tăng dần là:
(A) m - 2, m – 1, m; (B) m - 1, m, m + 1;
(C) m + 1, m, m -1; (D) m, m – 1, m - 2
Lời giải:
+) Ta thấy m + 1 > m nên (C) sai vì sắp xếp theo theo thứ tự tăng dần
+) Ta cũng có m > m – 1 nên (D) sai vì sắp xếp theo theo thứ tự tăng dần
Vì m ∈ N* nên m nhỏ nhất là 1, vì thế mà m – 2 không thực hiện được nên (A) sai
Đáp án cần chọn là: B
(A) P = {0; 1; 2; 3; 4; 5}
(B) P = { x ∈ N | x ≤ 5}
(C) P = { x ∈ N | x < 6}
(D) P = { x ∈ N | x < 5}
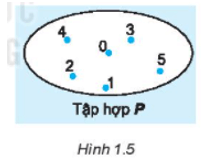
Lời giải:
Trong hình 1.5, tập hợp P có các phần tử thuộc tập hợp là: 0; 1; 2; 3; 4; 5 (các số này đều nằm trong vòng kín biểu diễn tập hợp P).
+ Ta viết tập hợp P bằng cách liệt kê các phần tử là: P = {0; 1; 2; 3; 4; 5} nên đáp án A đúng.
+ Vì các số 0; 1; 2; 3; 4; 5 là các số tự nhiên nhỏ hơn 6 (hoặc nhỏ hơn hoặc bằng 5).
+ Do đó bằng cách nêu dấu hiệu đặc trưng ta viết P = { x ∈ ℕ | x < 6} hoặc P = {x ∈ ℕ | x ≤ 5} nên đáp án B và C đúng.
+ Ở đáp án D, viết P = { x ∈ ℕ | x < 5} có nghĩa tập hợp P chứa các phần tử nhỏ hơn 5. Do đó phần tử 5 không thuộc tập hợp P.
Vậy D sai.
Đáp án cần chọn là: D
(A) 0; (B) 5;
(C) 7 (D) 11.
Lời giải:
A = { x ∈ N | x ≤ 7}. Tập hợp A bao gồm các số tự nhiên nhỏ hơn hoặc bằng 7 là: 0; 1; 2; 3; 4; 5; 6; 7.
Do vậy 11 ∉ A .
Đáp án cần chọn là: D
Bài 7 trang 28 sách bài tập Toán lớp 6 Tập 1: Câu nào trong các câu sau đây là câu đúng?
(A) Phép chia 687 cho 18 có số dư là 3;
(B) Phép chia 2 048 cho 128 có thương là 0;
(C) Phép chia 9 845 cho 125 có số dư là 130;
(D) Phép chia 295 cho 5 có thương là 300.
Lời giải:
Xét (A)
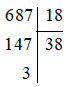
Vậy 687: 18 có số dư là 3 nên đáp án A đúng.
Kiểm tra cho (B), (C), (D) đều sai.
Đáp án cần chọn là: A
Bài 8 trang 29 sách bài tập Toán lớp 6 Tập 1: Lũy thừa với số mũ tự nhiên có tính chất nào sau đây?
(A) am.an = amn (B) am : an = am:n
(C) am.an = am+n (D) am.an = am-n
Lời giải:
Lũy thừa với số mũ tự nhiên có tính chất am.an = am+n và am : an = am-n. Vậy đáp án C đúng.
Đáp án cần chọn là: C
Bài 9 trang 29 sách bài tập Toán lớp 6 Tập 1: Lũy thừa 109 nhận giá trị nào sau đây?
(A) 100 000; (B) 1 000 000 000
(C) 1 000 000; (D) 10 000 000 000
Lời giải:
Ta có: 109 = 1 000 000 000
Đáp án cần chọn là: B
Bài tập
a) Mô tả tập hợp P bằng hai cách;
b) Biểu diễn các phần tử của tập P trên cùng một tia số.
Lời giải:
a) Các số tự nhiên lẻ lớn hơn 3 nhưng không lớn hơn 9 (nghĩa là nhỏ hơn hoặc bằng 9) là: 5; 7; 9
P là tập hợp các số tự nhiên lẻ, lớn hơn 3 nhưng không lớn hơn 9, do đó ta viết tập hợp P bằng hai cách như sau:
+) Cách 1: P = {5; 7; 9}
+) Cách 2: P = { x ∈ N| x lẻ và 3 < x ≤ 9}
b) Biểu diễn các phần tử P trên cùng một tia số là:
Gọi điểm A biểu diễn số 5, điểm B biểu diễn số 7 và điểm C biểu diễn số 9.
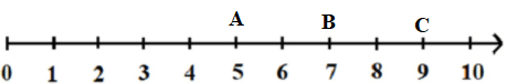
Lời giải:
Vì hiệu của chữ số hàng đơn vị và chữ số hàng chục bằng 8, do đó chữ số hàng đơn vị phải lớn hơn hoặc bằng 8.
+) Với chữ số hàng đơn vị là 8 thì chữ số hàng chục là: 8 – 8 = 0 (loại) vì chữ số hàng chục đứng đầu nên phải khác 0.
+) Với chữ số hàng đơn vị là 9 thì chữ số hàng chục là: 9 – 8 = 1 (thỏa mãn)
Vậy số cần tìm là 19.
Lời giải:
Phân tích 5 thành tổng của ba chữ số, ta có:
5 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3 = 1 + 1 + 3 = 1 + 2 + 2
Trường hợp 1: 5 = 0 + 0 + 5, ta được số 500 (loại vì 500 không phải là số lẻ)
Trường hợp 2: 5 = 0 + 1 + 4, vì số cần tìm là số lẻ, mà chữ số hàng trăm khác 0 nên số cần tìm là 401.
Trường hợp 3: 5 = 0 + 2 + 3, ta được số lẻ là 203
Trường hợp 4: 5 = 1 + 1 + 3, ta được các số lẻ là 113; 131; 311
Trường hợp 5: 5 = 1 + 2 + 2, ta được số lẻ 221.
Vậy các số cần tìm là: 401; 203; 113; 131; 311; 221.
Lời giải:
Phân tích 5 thành tổng của ba chữ số, ta có:
5 = 0 + 0 + 5 = 0 + 1 + 4 = 0 + 2 + 3 = 1 + 1 + 3 = 1 + 2 + 2
Trường hợp 1: 5 = 0 + 0 + 5, ta được số chẵn là 500
Trường hợp 2: 5 = 0 + 1 + 4, ta được số chẵn là 104; 140; 410
Trường hợp 3: 5 = 0 + 2 + 3, ta được số chẵn là 230; 320; 302
Trường hợp 4: 5 = 1 + 1 + 3, không có số chẵn
Trường hợp 5: 5 = 1 + 2 + 2, ta được số chẵn là 122; 212
Vậy các số cần tìm là: 500; 104; 140; 410; 230; 320; 302; 122; 212.
a) Mô tả tập E bằng cách liệt kê các phần tử của nó.
b) Gọi n là số lớn nhất trong tập E. Biểu diễn n thành tổng giá trị các chữ số của nó.
Lời giải:
a) Vì các số thuộc tập E có năm chữ số, trong khi tập các chữ số của chúng chỉ có bốn chữ số nên phải có một chữ số xuất hiện 2 lần.
+) Với chữ số 1 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 11 357
+) Với chữ số 3 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 357
+) Với chữ số 5 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 557
+) Với chữ số 7 xuất hiện 2 lần ta được số sắp xếp theo thứ tự không giảm là: 13 577
Vậy E = {11 357; 13 357; 13 557; 13 577}
b) Vì 11 357 < 13 357 < 13 557 < 13 577 nên 13 577 là số lớn nhất của tập E.
Vì n là số lớn nhất trong tập E nên n = 13 577
+ Chữ số 1 nằm ở hàng chục nghìn và có giá trị bằng 1 x 10 000
+) Chữ số 3 nằm ở hàng nghìn và có giá trị bằng 3 x 1 000
+) Chữ số 5 nằm ở hàng trăm và có giá trị bằng 5 x 100
+) Chữ số 7 nằm ở hàng chục và có giá trị bằng 7 x 10
+) Chữ số 7 nằm ở hàng đơn vị và có giá trị bằng 7 x 1
Do đó biểu diễn n thành tổng các giá trị của nó là:
13 577 = 1 x 10 000 + 3 x 1 000 + 5 x 100 + 7 x 10 + 7 x 1
Lời giải:
Các số có hai chữ số trong đó có mặt chữ số 2 là: 20; 21; 22; 23; 24; 25; 26; 27; 28; 29; 12; 32; 42; 52; 62; 72; 82; 92.
Vậy có 18 số có hai chữ số trong đó có mặt chữ số 2.
Lời giải:
Số bạn được đúng một điểm 10 là:
42 – 39 = 3 (bạn)
Số bạn được đúng hai điểm 10 là:
39 – 14 = 25 (bạn)
Số bạn được đúng ba điểm 10 là:
14 – 5 = 9 (bạn)
Số bạn được đúng bốn điểm 10 là 5.
Tổng số điểm 10 của cả lớp 6A là:
3. 1 + 25. 2 + 9. 3 + 5. 4 = 100 (điểm 10)
Vậy lớp 6A được tất cả 100 điểm 10.
Lời giải:
Bạn Quang đã viết các tích riêng thẳng cột: chữ số hàng đơn vị dưới chữ số hàng đơn vị; chữ số hàng chục dưới chữ số hàng chục; … Do đặt sai vị trí các tích riêng nên 13 783 là tổng các tích riêng.
Ta có tổng các tích riêng là:
a. 2 + a. 5 + a. 4 = a. (2 + 5 + 4) = a. 11.
Do đó: a. 11 = 13 783
Suy ra a = 13 783: 11 = 1 253
Tích đúng là 1 253. 254
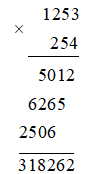
Vậy tích đúng là 1 253. 254 = 318 262.
Lời giải:
S = 1 + 2 – 3 – 4 + 5 + 6 – 7 – 8 + 9 + 10 - … + 2 018 – 2 019 – 2 020 + 2 021
= 1 + (2 – 3 – 4 + 5) + (6 – 7 – 8 + 9) + … + (2 018 – 2 019 – 2 020 + 2 021)
= 1 + [(5 + 2) – (3 + 4)] + [(6 + 9) – (7 + 8)] + … + [(2 018 + 2 021) – (2 019 + 2 020)]
= 1 + (7 – 7) + (15 – 15) + … + (4 039 – 4 039)
= 1 + 0 + 0 + … + 0
= 1.
Lời giải:
Gọi số chia và thương lần lượt là b và q (b; q ∈ ℕ, b ≠0).
Như vậy 89 : b = q (dư 12) và b > 12 (số chia lớn hơn số dư).
Từ đó 89 = bq + 12. Suy ra bq = 89 – 12 = 77 = 7 . 11 = 77 . 1
Mà b > 12 nên b = 77 và q = 1.
Do đó 89 : 77 = 1 (dư 12).
Vậy số chia bằng 77, thương bằng 1.
CÔNG TY TNHH ĐẦU TƯ VÀ DỊCH VỤ GIÁO DỤC VIETJACK
- Người đại diện: Nguyễn Thanh Tuyền
- Số giấy chứng nhận đăng ký kinh doanh: 0108307822, ngày cấp: 04/06/2018, nơi cấp: Sở Kế hoạch và Đầu tư thành phố Hà Nội.
© 2021 Vietjack. All Rights Reserved.
