Với giải sách bài tập Toán 6 Bài 2: Cách ghi số tự nhiên sách Kết nối tri thức hay, chi tiết giúp học sinh dễ dàng xem và so sánh lời giải từ đó biết cách làm bài tập trong SBT Toán 6. Mời các bạn đón xem:

Giải SBT Toán lớp 6 Bài 2: Cách ghi số tự nhiên

Bài 1.8 trang 9 sách bài tập Toán lớp 6 Tập 1: Một số tự nhiên có hai chữ số, trong đó chữ số hàng chục lớn hơn chữ số hàng đơn vị là 9. Đó là số nào?

Lời giải:

Gọi chữ số hàng đơn vị của số cần tìm là a (a ∈ ℕ, 0 ≤ a ≤ 9)

Giả sử chữ số hàng đơn vị là 1, vì chữ số hàng chục lớn hơn chữ số hàng đơn vị là 9 do đó chữ số hàng chục là: 1 + 9 = 10, điều đó không xảy ra.

Nếu chữ số hàng đơn vị lớn hơn 1 thì chữ số hàng chục lớn hơn 10, điều đó không xảy ra.

Vì thế a = 0 hay chữ số hàng đơn vị là 0

Chữ số hàng chục là: 0 + 9 = 9

Vậy số cần tìm có hai chữ số là 90.

Bài 1.9 trang 9 sách bài tập Toán lớp 6 Tập 1: Gọi A là tập hợp các số tự nhiên có hai chữ số, trong đó chữ số hàng đơn vị lớn hơn chữ số hàng chục là 3. Hãy mô tả tập hợp A bằng cách liệt kê các phần tử của nó.

Lời giải:

Gọi số tự nhiên có hai chữ số là ab— (a, b ∈ ℕ, 1 ≤ a ≤ 9, 0 ≤ b ≤ 9)

Vì chữ số hàng đơn vị lớn hơn chữ số hàng chục là 3 nên b ≥ 3 nên ta có bảng sau:

Các số tự nhiên có hai chữ số thỏa mãn yêu cầu bài toán là: 14; 25; 36; 47; 58; 69

Do đó tập hợp A được viết: A = {14; 25; 36; 47; 58; 69}.

Bài 1.10 trang 9 sách bài tập Toán lớp 6 Tập 1: Hãy viết số tự nhiên lớn nhất có 6 chữ số.

Lời giải:

Một số tự nhiên lớn nhất có 6 chữ số thì các chữ số của số đó phải đạt giá trị lớn nhất có thể.

Vì chữ số đầu tiên lớn nhất thì chữ số đầu tiên phải là 9

Năm chữ số tiếp theo lớn nhất là số 9

Vậy số tự nhiên lớn nhất có 6 chữ số: 999 999.

Bài 1.11 trang 9 sách bài tập Toán lớp 6 Tập 1: Số tự nhiên nào lớn nhất có 6 chữ số khác nhau?

Lời giải:

Một số có 6 chữ số khác nhau là số lớn nhất thì:

Chữ số đầu tiên của nó phải là số lớn nhất tức là số 9

Chữ số kế tiếp phải là số lớn nhất khác 9 tức là số 8

Chữ số kế tiếp phải là số lớn nhất khác 9 và 8 tức là số 7

Chữ số kế tiếp phải là số lớn nhất khác 9; 8 và 7 tức là số 6

Chữ số kế tiếp phải là số lớn nhất khác 9; 8; 7; và 6 tức là số 5

Chữ số hàng đơn vị phải lớn nhất khác 9; 8; 7; 6; 5 tức là số 4

Vậy số tự nhiên lớn nhất có sáu chữ số khác nhau: 987 654.

Bài 1.12 trang 9 sách bài tập Toán lớp 6 Tập 1: Cho tập hợp P = {0; 4; 9}. Hãy viết các số tự nhiên:

a) Có ba chữ số và tập hợp các chữ số của nó là tập P;

b) Có ba chữ số lấy trong tập P.

Lời giải:

a) Vì số tự nhiên có ba chữ số và tập hợp các chữ số của nó là tập P nghĩa là số tự nhiên có ba chữ số khác nhau được tạo thành từ ba chữ số 0; 4; 9

Gọi số tự nhiên có ba chữ số khác nhau là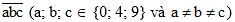 

Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9.

+) Với a = 4, ta có các số thỏa mãn là: 409; 490

+) Với a = 9, ta có các số thỏa mãn là: 904; 940

Vậy ta được các số thỏa mãn đề bài là: 409; 490; 904; 940.

b) Vì số tự nhiên có ba chữ số lấy trong tập P thì các số cần tìm được viết bởi 0; 4; 9 nhưng không nhất thiết có mặt cả ba chữ số đó. Vậy mỗi chữ số có thể không có mặt hoặc có mặt 1; 2 hoặc 3 lần.

Gọi số tự nhiên có ba chữ số là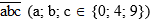 

Vì chữ số hàng trăm khác 0 nên a = 4 hoặc a = 9

Trường hợp 1: a = 4

+) Với a = 4, b = 0 ta có ba số: 400; 404; 409

+) Với a = 4, b = 4 ta được ba số: 440; 444; 449

+) Với a = 4, b = 9 ta được ba số: 490; 494; 499

Trường hợp 2: Với a = 9

+) Với a = 9, b = 0 ta được ba số: 900; 904; 909

+) Với a = 9; b = 4 ta được ba số: 940; 944; 949

+) Với a = 9, b = 9 ta được ba số: 990; 994; 999

Vậy các số thỏa mãn điều kiện đề bài là: 400; 404; 409; 440; 444; 449; 490; 494; 499; 900; 904; 909; 940; 944; 949; 990; 994; 999.

Bài 1.13 trang 9 sách bài tập Toán lớp 6 Tập 1: Viết tập hợp các số tự nhiên có ba chữ số mà tổng các chữ số của nó bằng 4.

Lời giải:

Gọi số tự nhiên có ba chữ số là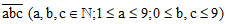 

Vì tổng các chữ số của nó bằng 4 hay a + b + c = 4 nên các chữ số đều nhỏ hơn hoặc bằng 4. Do a đứng ở hàng trăm nên a ∈ {1;2;3;4}

Trường hợp 1: Với a = 4, ta có: 4 + b + c = 4 ⇒ b + c = 0, ta được b = 0 và c = 0. Do đó ta lập được 1 số là 400.

Trường hợp 2: Với a = 3, ta có: 3 + b + c = 4 ⇒ b + c = 1 do đó b ≤ 1

+) Với b = 0 thì c = 1 ta được số 301

+) Với b = 1 thì c = 0 ta được số 310

Trường hợp 3: Với a = 2, ta được: 2 + b + c = 4 ⇒ b + c = 2 do đó b ≤ 2

+) Với b = 0 thì c = 2, ta được số 202

+) Với b = 1 thì c = 1, ta được số 211

+) Với b = 2 thì c = 0, ta được số 220

Trường hợp 4: Với a = 1, ta được: 1 + b + c = 4 ⇒ b + c = 3 do đó b ≤ 3

+) Với b = 0 thì c = 3, ta được số 103

+) Với b = 1 thì c = 2, ta được số 112

+) Với b = 2 thì c = 1, ta được số 121

+) Với b = 3 thì c = 0, ta được số 130

Giả sử tập hợp các số tự nhiên có ba chữ số mà tổng các chữ số của nó bằng 4 là A.

Vậy ta viết tập hợp A là:

A = {400; 310; 301; 202; 211; 220; 103; 112; 121; 130}.

Bài 1.14 trang 9 sách bài tập Toán lớp 6 Tập 1: Từ một số tự nhiên n có ba chữ số cho trước, ta sẽ được số nào nếu:

a) Viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó?

b) Viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó?

Lời giải:

a) Gọi số cần tìm là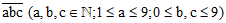 

Khi viết thêm chữ số 0 vào bên phải số đó ta được số: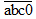 

Ta có: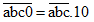 

Vậy nếu viết thêm chữ số 0 vào sau (tận cùng bên phải) số đó ta được số mới gấp 10 lần số đã cho.

b) Gọi số cần tìm là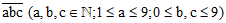 

Khi viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó ta được số: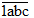 

Ta có: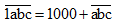 

Vậy nếu viết thêm chữ số 1 vào trước (tận cùng bên trái) số đó ta được số mới hơn số đã cho 1 000 đơn vị.

Bài 1.15 trang 9 sách bài tập Toán lớp 6 Tập 1: Viết thêm chữ số 9 vào số 812 574 để thu được:

a) Số lớn nhất;

b) Số nhỏ nhất.

Lời giải:

a) Vì chữ số 9 là chữ số lớn nhất nên viết thêm chữ số 9 đứng đầu hay đứng ở hàng triệu ta được số 9 812 574 là số lớn nhất.

b) Vì chữ số 9 là chữ số lớn nhất nên viết thêm chữ số 9 đứng ở hàng đơn vị ta được số 

8 125 749 là số nhỏ nhất.

Bài 1.16 trang 10 sách bài tập Toán lớp 6 Tập 1: Viết thêm chữ số 6 vào số 812 574 để thu được:

a) Số lớn nhất; 

b) Số nhỏ nhất.

Lời giải:

a) Để khi viết thêm chữ số 6 vào số 812 574 thì số đó thành số lớn nhất mà 6 < 8 nên chữ số 6 phải nằm ở hàng lớn nhất sau chữ số 8 nên chữ số 6 nằm ở hàng trăm nghìn

Vậy khi đó số đó là: 8 612 574.

b) Để khi viết thêm chữ số 6 vào số 812 574 thì số đó thành số nhỏ nhất mà 6 < 8 nên chữ số 6 phải nằm ở hàng triệu.

Vậy khi đó số đó là: 6 812 574.

Bài 1.17 trang 10 sách bài tập Toán lớp 6 Tập 1: Cho số 728 031. Hãy hoàn thiện bảng sau:

Lời giải:

+) Chữ số 7 đứng ở hàng trăm nghìn nên có giá trị 7 x 100 000

+) Chữ số 2 đứng ở hàng chục nghìn nên có giá trị 2 x 10 000

+) Chữ số 0 đứng ở hàng trăm nên có giá trị 0 x 100 

+) Chữ số 3 đứng ở hàng chục nên có giá trị 3 x 10

+) Chữ số 1 đứng ở hàng đơn vị nên có giá trị 1 x 1

Vậy em điền được như sau: 

Bài 1.18 trang 10 sách bài tập Toán lớp 6 Tập 1: Viết 2 975 002 thành tổng giá trị các chữ số của nó.

Lời giải:

+) Chữ số 2 đứng ở hàng triệu nên có giá trị 2 x 1 000 000

+) Chữ số 9 đứng ở hàng trăm nghìn nên có giá trị 9 x 100 000

+) Chữ số 7 đứng ở hàng chục nghìn nên có giá trị 7 x 10 000

+) Chữ số 5 đứng ở hàng nghìn nên có giá trị 5 x 1 000

+) Chữ số 0 đứng ở hàng trăm nên có giá trị 0 x 100 

+) Chữ số 0 đứng ở hàng chục nên có giá trị 0 x 10

+) Chữ số 2 đứng ở hàng đơn vị nên có giá trị 2 x 1

Do đó:  2 975 002 = 2 x 1 000 000 + 9 x 100 000 + 7 x 10 000 + 5 x 1 000 + 0 x 100 + 

0 x 10 + 2 x 1.

Bài 1.19 trang 10 sách bài tập Toán lớp 6 Tập 1: Đọc các số La Mã XIV, XVI, XIX và XXI.

Lời giải:

+) Số La Mã XIV đọc là: Mười bốn

+) Số La Mã XVI đọc là: Mười sáu

+) Số La Mã XIX đọc là: Mười chín

+) Số La Mã XXI đọc là: Hai mươi mốt.

Bài 1.20 trang 10 sách bài tập Toán lớp 6 Tập 1: Viết các số sau bằng số La Mã: 14; 24 và 26.

Lời giải:

+) 14 viết bằng số La Mã là: XIV

+) 24 viết bằng số La Mã là: XXIV

+) 26 viết bằng số La Mã là: XXVI.

Bài 1.21 trang 10 sách bài tập Toán lớp 6 Tập 1: Có 12 que tính xếp thành một phép cộng sai như sau:

Hãy đổi chỗ chỉ 1 que tính để được phép cộng đúng. Em tìm được mấy cách làm?

Lời giải:

Ta có: IV = 4; V = 5; 4 + 5 = 9 nên phép cộng trên là 4 + 5 = 11 (XI là 11) là sai, do đó ta di chuyển 1 que diêm I từ bên phải qua bên trái của XI thành IX để được số 9 ta có được phép tính đúng là:

Ngoài ra ta thấy 6 + 5 = 11, nên ta chi duyển 1 que diêm I từ bên trái qua bên phải của IV thành VI để được số 6 ta có được phép tính đúng là:

Lý thuyết Cách ghi số tự nhiên

1. Hệ thập phân

+ Cách ghi số tự nhiên trong hệ thập phân

- Trong hệ thập phân, mỗi số tự nhiên được viết dưới dạng một dãy những chữ số lấy trong 10 chữ số 0; 1; 2; 3; 4; 5; 6; 7; 8 và 9; vị trí của các chữ số trong dãy gọi là hàng.

- Cứ 10 đơn vị ở một hàng thì bằng 1 đơn vị ở hàng liền trước nó. Chẳng hạn, 10 chục thì bằng 1 trăm; 10 trăm thì bằng 1 nghìn; …

Chú ý: Khi viết các số tự nhiên ta quy ước:

1. Với các số tự nhiên khác 0, chữ số đầu tiên (từ trái sang phải) khác 0.

2. Để dễ đọc với các số có bốn chữ số ta viết tách riêng từng lớp. Mỗi lớp là một nhóm ba chữ số kể từ phải sang trái.

Ví dụ 1. Hãy viết tất cả các số tự nhiên có ba chữ số khác nhau chỉ dùng 3 chữ số 0; 3; 5. Đọc mỗi số đã viết được.

Lời giải

Các số tự nhiên có ba chữ số khác nhau từ ba số 0; 3; 5 là:

305; 350; 503; 530.

Cách đọc:

305: ba trăm linh năm;

350: ba trăm năm mươi;

503: năm trăm linh ba;

530: năm trăm ba mươi.

+ Mỗi số tự nhiên viết trong hệ thập phân đều biểu diễn được thành tổng giá trị các chữ số của nó. Chẳng hạn như số có ba chữ số 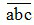(a, b, c ∈ N) được viết dưới dạng tổng giá trị các chữ số của nó như sau: 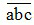= a x 100 + b x 10 + c

Ví dụ 2. 

a) Viết sô 32009 thành tổng các chữ số của chúng.

c) Cho số 1256934, chữ số 5 trong số đã cho nằm ở hàng nào và có giá trị bao nhiêu?

Lời giải

a) 32009 = 3 x 10000 + 2 x 1000 + 0 x 100 + 0 x 10 + 9.

b) Chữ số 5 trong số đã cho nằm ở hàng chục nghìn và có giá trị .

2. Số La Mã

Để viết các số La Mã không quá 30, ta dùng các kí tự I, V và X (gọi là những số La Mã).

Ba chữ số đó cộng với hai cụm chữ số là IV và IX là năm thành phần dùng để ghi số La Mã. 

Giá trị của mỗi thành phần được ghi lại trong bảng sau và không thay đổi dù đứng ở bất kì vị trí nào:

+ Dưới đây là các số La Mã biểu diễn các số từ 1 đến 10:

+ Để biểu diễn các số từ 11 đến 20, ta thêm X vào bên trái mỗi số từ I đến X:

+ Để biểu diễn các số từ 21 đến 30, ta thêm XX vào bên trái mỗi số từ I đến X:

Ví dụ 3:

a) Viết các số 17; 23 và 8 bằng số La Mã.

b) Đọc các số La Mã XXIX, XIV, VII.

Lời giải

a) Số La Mã biểu diễn cho số 17 là: XVII;

Số La Mã biểu diễn cho số 23 là: XXIII;

Số La Mã biểu diễn cho số 8 là: VIII.

b) Đọc:

XXIX: Hai mươi chín;

XIV: Mười bốn;

VII: Bảy.