Tài liệu chuyên đề Tính đối xứng của hình phẳng trong tự nhiên Toán lớp 6 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 6. 

Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 6 Kết nối tri thức bản word có lời giải chi tiết:

B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)

B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây

Xem thử tài liệu tại đây: Link tài liệu

Chuyên đề Tính đối xứng của hình phẳng trong tự nhiên

Tài liệu gồm 2 chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hình có tâm đối xứng :

CHUYÊN ĐỀ 2: HÌNH CÓ TÂM ĐỐI XỨNG

PHẦN I. TÓM TẮT LÍ THUYẾT

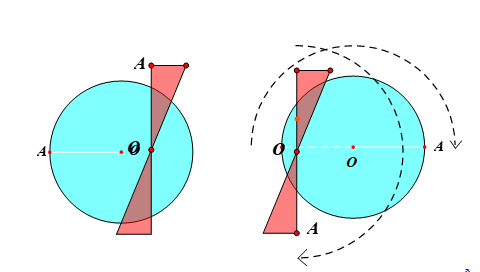
Định nghĩa: Mỗi hình có một điểm O, mà khi quay hình đó quanh điểm O đúng một nửa vòng thì hình thu được “chồng khít” với chính nó ở vị trí ban đầu (trước khi quay).

   Những hình như thế được gọi là hình có tâm đối xứng và điểm \[O\] được gọi là tâm đối xứng của hình.

   Ví dụ hình tròn tâm \[O\] hay chong chóng hai cánh quay quanh tâm (trục)

PHẦN II. CÁC DẠNG BÀI.

Dạng 1. Kiểm tra hình có tâm đối xứng hay không

I. Phương pháp giải.

            Nói đến tâm của hình (ta hiểu là điểm nằm chính giữa hình). Để kiểm tra xem điểm đó có là tâm đối xứng của hình hay không thì ta lấy một điểm bất kỳ trên (hay trong) hình, lấy đối xứng qua tâm thì ta được một điểm:

            + Nếu điểm đó vẫn thuộc hình thì hình đó có tâm đối xứng.

+ Nếu điểm đó không thuộc hình thì hình đó không có tâm đối xứng.

II. Bài toán.

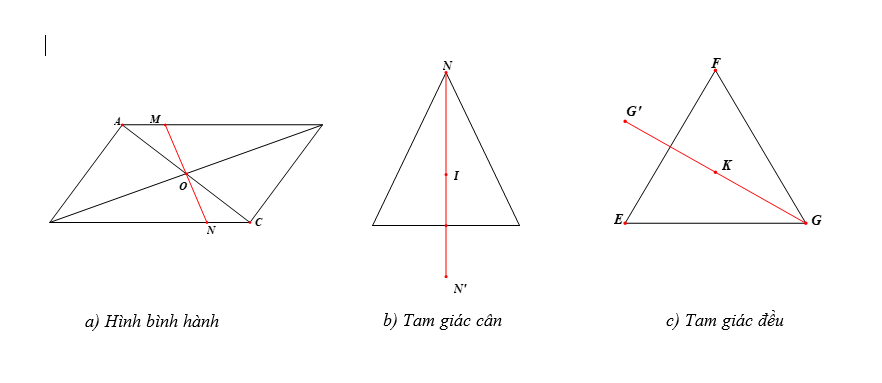
Bài 1. Cho các hình vẽ sau. Hãy cho biết hình nào là hình có tâm đối xứng?

Lời giải

            a) Với hình bình hành dễ thấy tâm \[O\] là tâm đối xứng của hình bình hành. Vì với một điểm \[M\] bất kỳ thuộc hình bình hành khi lấy đối xứng qua tâm \[O\] ta được điểm \[N\] (đo \[OM = ON\]), vẫn thấy điểm \[N\] thuộc hình bình hành.

            b) Với tam giác cân \[MNP\] ta phán đoán \[I\] là tâm đối xứng của hình. Ta chọn điểm \[N\] thuộc tam giác \[MNP\], khi lấy đối xứng qua \[I\] ta được điểm  (đo ), nhưng điểm  không thuộc tam giác \[MNP\]. Do đó tam giác cân \[MNP\] là hình không có tâm đối xứng.

c) Với tam giác đều \[{\rm{EF}}G\] ta phán đoán \[K\] là tâm đối xứng của hình. Ta chọn điểm \[G\] thuộc tam giác \[{\rm{EF}}G\], khi lấy đối xứng qua \[K\] ta được điểm \[G'\] (đo ), nhưng điểm \[G'\] không thuộc tam giác \[{\rm{EF}}G\]. Do đó tam giác đều \[{\rm{EF}}G\] là hình không có tâm đối xứng.

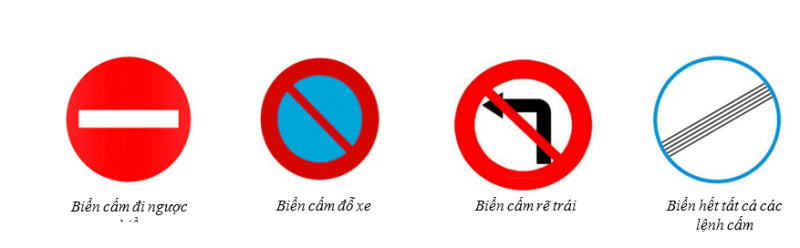
Bài 2. Biển báo giao thông nào có tâm đối xứng trong các biển báo sau?

Lời giải

Biển báo giao thông có tâm đối xứng là: Biển cấm đi ngược chiều, biển cấm đỗ xe, biển hết tất cả các lệnh cấm

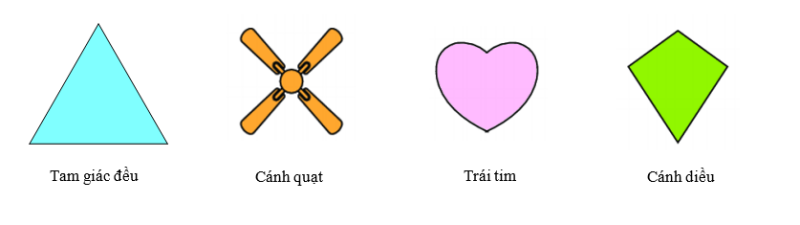
Bài 3. Trong các hình dưới đây, em hãy chỉ ra:

            a) Những hình có tâm đối xứng;

            b) Những hình có trục đối xứng.

 Lời giải

a) Hình có tâm đối xứng là: cánh quạt.

b) Những hình có trục đối xứng là: tam giác đều, trái tim, cánh diều.

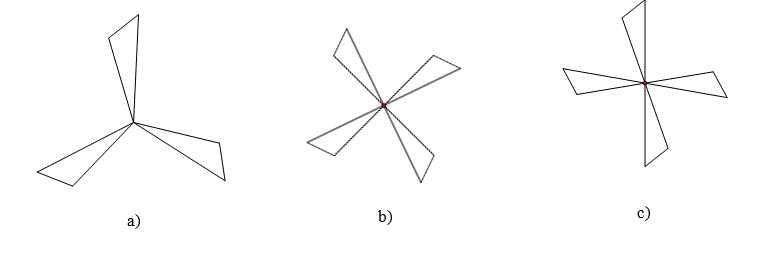
Bài 4. Hình nào dưới đây là hình có tâm đối xứng?

Lời giải

            Hình b là hình có tâm đối xứng.

Bài 5. Trong các biển báo giao thông sau, biển báo nào chỉ có trục đối xứng, biển báo nào vừa có tâm đối xứng, vừa có trục đối xứng?

Lời giải

            Biển báo chỉ có trục đối xứng là: e, f, h.

Biển báo vừa có tâm đối xứng, vừa có trục đối xứng: a, b, c, d

Dạng 2. Tâm đối xứng của hình

I.Phương pháp giải.

            Đối với những hình có tâm đối xứng thì hình đó có số cạnh (viền ngoài) là chẵn, hoặc trong thiên nhiên hình ảnh của bông hoa có tâm đối xứng nằm ở giữa (nhị hay nhụy hoa), hình ảnh của cỏ bốn lá cũng có tâm đối xứng.

            Đối với các hình có số cạnh bằng nhau (số cạnh chẵn) thì tâm đối xứng chính là giao của các đường chéo.

II.Bài toán.

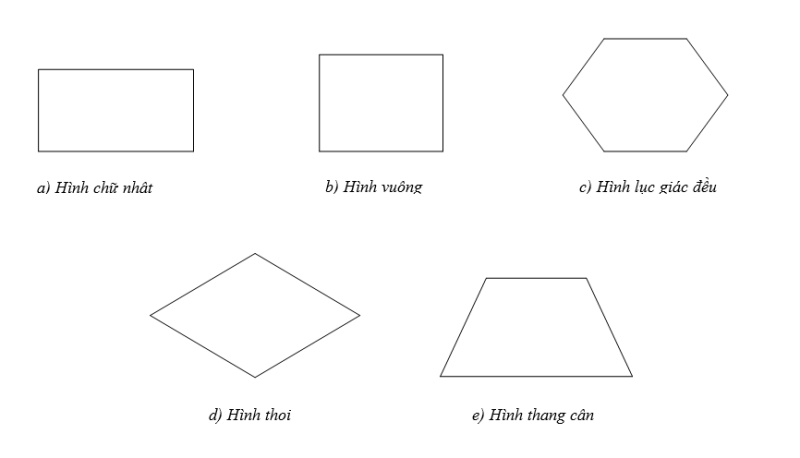
Bài 1. Cho hình vẽ sau, hãy cho biết hình nào có tâm đối xứng và xác định tâm đối xứng của hình đó?

Lời giải

a) Hình chữ nhật có tâm đối xứng chính là giao điểm \[A\]của hai đường chéo.

b) Hình vuông có tâm đối xứng là giao điểm \[B\] của hai đường chéo.

c) Hình lục giác đều có tâm đối xứng là giao điểm \[C\] của các đường chéo.

d) Hình thoi có tâm đối xứng là giao điểm \[D\] của hai đường chéo.

e) Hình thang cân không có tâm đối xứng vì với một điểm \[P\] bất kỳ thuộc hình bình hành khi lấy đối xứng qua tâm \[O\] ta được điểm \[P'\], nhưng điểm \[P'\] không thuộc hình thang cân. 

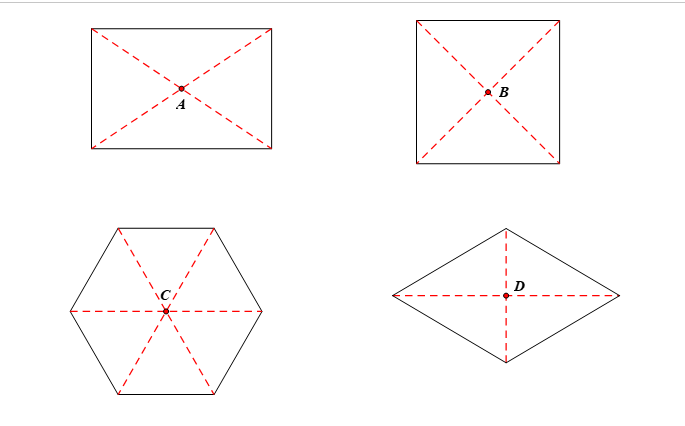
Bài 2. Trong mỗi hình dưới đây, điểm \[O\] có phải là tâm đối xứng không?

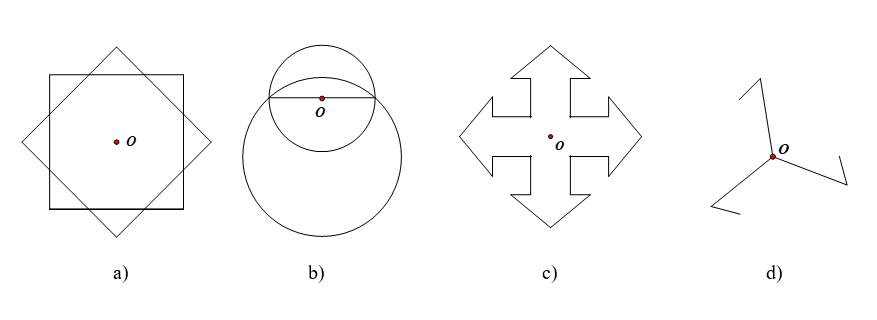
 Lời giải

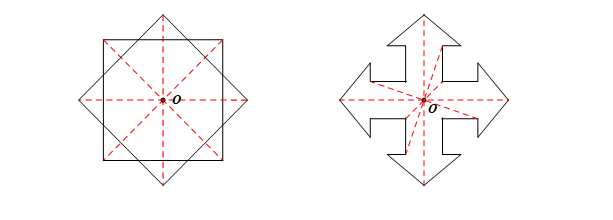
Điểm \[O\] là tâm đối xứng của các hình a,c

  
Bài 3. Hình nào dưới đây có tâm đối xứng? Em hãy xác định tâm đối xứng (nếu có) của chúng.

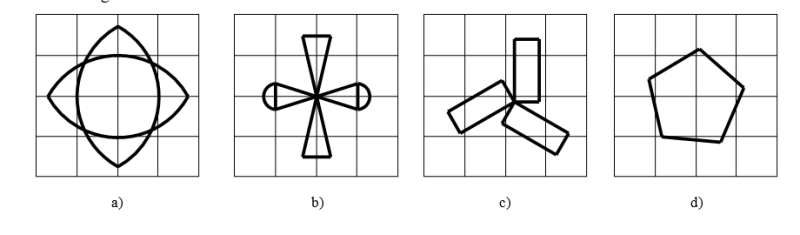
Lời giải

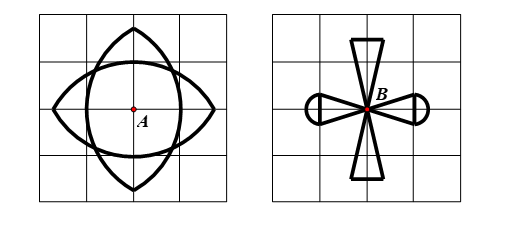
Các hình có tâm đối xứng là hình a, b.

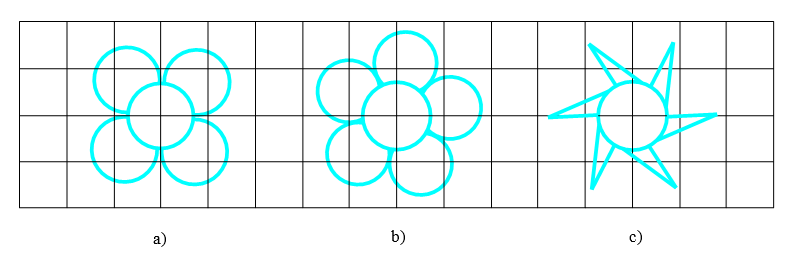
Bài 4. Trong các hình dưới đây, hình nào dưới đây có tâm đối xứng? Em hãy xác định tâm đối xứng (nếu có) của chúng.

Lời giải           

Các hình có tâm đối xứng là hình a, c.