Tài liệu chuyên đề Một số hình phẳng trong thực tiễn Toán lớp 6 sách Kết nối tri thức gồm lý thuyết và các dạng bài tập từ cơ bản đến nâng cao với phương pháp giải chi tiết và bài tập tự luyện đa dạng giúp Giáo viên có thêm tài liệu giảng dạy Toán 6.
Chỉ từ 450k mua trọn bộ Chuyên đề dạy thêm Toán 6 Kết nối tri thức bản word có lời giải chi tiết:
B1: Gửi phí vào tài khoản0711000255837 - NGUYEN THANH TUYEN - Ngân hàng Vietcombank (QR)
B2: Nhắn tin tới zalo Vietjack Official - nhấn vào đây
Xem thử tài liệu tại đây: Link tài liệu
Chuyên đề Một số hình phẳng trong thực tiễn
Tài liệu gồm 2 chuyên đề nhỏ, mời bạn đọc xem thử nội dung Chuyên đề Hình bình hành, hình thoi :
CHUYÊN ĐỀ 2: HÌNH BÌNH HÀNH, HÌNH THOI
PHẦN I. TÓM TẮT LÍ THUYẾT.
1. Hình bình hành
a) Nhận biết hình bình hành
Trong hình bình hành: 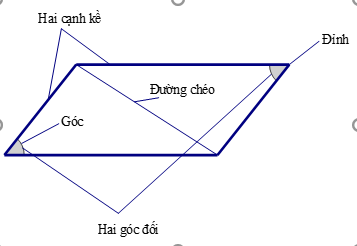
- Các cạnh đối song song với nhau.
- Các cạnh đối bằng nhau
- Các góc đối bằng nhau\[ABCD\]
- hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Cụ thể: Hình bình hành có \[AC\] cắt \[BD\]tại \[O\]:
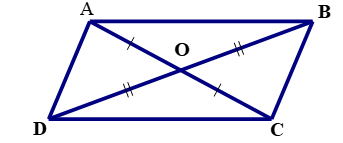
+ \[AB\parallel CD;AD\parallel BC\]
+ \[AB = CD;AD = BC\]
+ \[\widehat A = \widehat C;\widehat B = \widehat D\]
+ \[OA = OC;OB = OD\]
b) Chu vi và diện tích hình bình hành
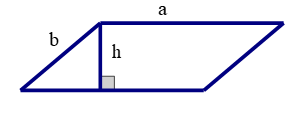
- Chu vi hình bình hành: \[C = 2\left( {a + b} \right)\]
- Diện tích hình thoi: \[S = a.h\], trong đó \[a\] là cạnh, \[h\] là chiều cao tương ứng.
2. Hình thoi
a) Nhận biết hình thoi
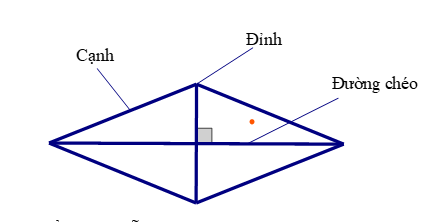
Trong một hình thoi:
- Bốn cạnh bằng nhau.
- Các cạnh đối song song với nhau.
- Các góc đối bằng nhau.
- Hai đường chéo vuông góc với nhau, cắt nhau tại trung điểm của mỗi đường.
Cụ thể: Cho hình thoi \[ABCD\] có \[AC\] cắt \[BD\] tại \[O\].
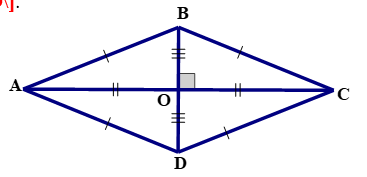
+ \[AB = BC = CD = DA\]
+ \[AB\parallel CD;AD\parallel BC\]
+ \[\widehat A = \widehat C;\widehat B = \widehat D\]
+ \[AC \bot BD;OA = OC;OB = OD\]
Nhận xét: Hình thoi là hình bình hành.
b) Chu vi và diện tích hình thoi
- Chu vi hình thoi \[C = 4a\]
- Diện tích hình thoi \[S = \frac{1}{2}{d_1}{d_2}\], trong đó \[{d_1};{d_2}\] là độ dài hai đường chéo.
PHẦN II. CÁC DẠNG BÀI.
A. Hình bình hành
Dạng 1: Nhận biết hình bình hành
I. Phương pháp giải.
Các dấu hiệu nhận biết hình bình hành:
1. Tứ giác có các cạnh đối song song là hình bình hành.
2. Tứ giác có các cạnh đối bằng nhau là hình bình hành.
3. Tứ giác có một cặp cạnh đối vừa song song vừa bằng nhau là hình bình hành.
4. Tứ giác có các góc đối bằng nhau là hình bình hành.
5. Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành.
II. Bài toán.
Bài 1:
Các tứ giác ở hình vẽ bên dưới có là hình bình hành không? Vì sao?
Lời giải
Cả ba tứ giác là hình bình hành
- Tứ giác ABCD là hình bình hành vì có AB // CD và AB = CD = 3 (dấu hiệu nhận biết 3)
- Tứ giác EFGH là hình bình hành vì có EH // FG và EH = FH = 3 (dấu hiệu nhận biết 3)
- Tứ giác MNPQ là hình bình hành vì có MN = PQ và MQ = NP (dấu hiệu nhận biết 2)
Chú ý:
- Với các tứ giác ABCD, EFGH còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 2.
- Với tứ giác MNPQ còn có thể nhận biết là hình bình hành bằng dấu hiệu nhận biết 5.
Dạng 2: Cách vẽ hình bình hành
I. Phương pháp giải.
Dựa vào các tính chất của hình bình hành để vẽ hình bình hành.
II. Bài toán.
Bài 1:
Vẽ hình bình hành \[ABCD\] có \[AB = 6cm\],\[BC = 4cm\].
Lời giải
|
Bước 1. Vẽ đoạn thẳng \[AB = 6cm\] |
|
|
Bước 2. Vẽ đường thẳng đi qua B. Trên đường thẳng đó lấy điểm C sao cho \[BC = 4cm\] |
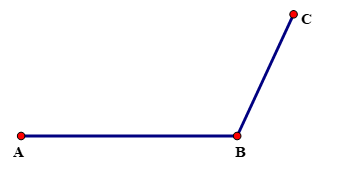 |
|
Bước 3. Vẽ đường thẳng đi qua A và song song với BC, đường thẳng qua C và song song với AB. Hai đường thẳng này cắt nhau tại D, ta được hình bình hành ABCD. |
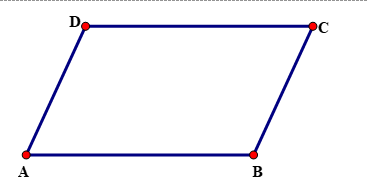 |
Bài 2:
Cho trước hai đoạn thẳng AB và CD như hình vẽ. Vẽ hình bình hành ABCD nhận AB và CD làm cạnh.
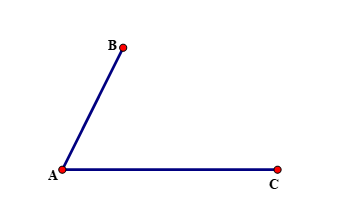
Lời giải
|
Bước 1. - Vẽ một phần đường tròn tâm B bán kính AC. - Vẽ một phần đường tròn tâm C bán kính AB. Hai đườngtròn này cắt nhau tại D. Bước 2. Nối D với B, D với C, ta được hình bình hành ABCD. |
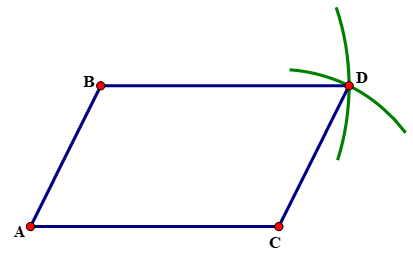 |
Bài 3:
Vẽ hình bình hành có độ dài một cạnh bằng \[5cm\], một cạnh bằng \[3cm\].
Lời giải
|
Bước 1. Vẽ đoạn thẳng \[AB = 5cm\] |
|
|
Bước 2. Vẽ đường thẳng đi qua \(B\). Trên đường thẳng đó lấy điểm \(C\) sao cho \[BC = 3cm\] |
 |
|
Bước 3. Vẽ đường thẳng đi qua \(A\) và song song với \(BC\), đường thẳng qua \(C\) và song song với \(AB\). Hai đường thẳng này cắt nhau tại \(D\), ta được hình bình hành \[ABCD\]. |
 |
Dạng 3. Tính chu vi và diện tích hình bình hành
I. Phương pháp giải.
Dựa vào công thức tính chu vi và diện tích hình bình hành; mối quan hệ giữa các cạnh của hình bình hành.
II. Bài toán.
Bài 1:
Cho hình bình hành có cạnh đáy là bằng \[15{\rm{ cm}}\]và cạnh bên bằng \[{\rm{7 cm}}\]và có chiều cao là \[5{\rm{ cm}}\]. Hãy tính chu vi và diện tích hình bình hành đó.
Lời giải
Chu vi của hình bình hành là: \[C = 2.(15 + 7) = 44{\rm{ }}(cm)\]
Diện tích hình bình hành là: \[S = 15.5 = 75{\rm{ (c}}{{\rm{m}}^2})\]
Bài 2:
Cho hình bình hành có chu vi là \[384{\rm{ cm}}\], độ dài cạnh đáy bằng 5 lần cạnh kia, bằng 8 lần chiều cao. Tính diện tích của hình bình hành.
Lời giải
Gọi cạnh bên \(a\), ta có cạnh đáy \[5a\], chiều cao \(\frac{{5a}}{8}\)
Chu vi hình bình hành = (cạnh bên + cạnh đáy) x 2 = 384
suy ra \[\left( {a + 5a} \right){\rm{ x }}2 = 384\] hay \[a{\rm{ }} = {\rm{ }}30cm\]
Do đó, cạnh bên \[32cm\], cạnh đáy \[160cm\], chiều cao \(20\,cm\)
Vì thế, diện tích hình bình hành là \[20{\rm{ x }}160 = 3600{\rm{ }}\left( {c{m^2}} \right)\]
Bài 3:
Một mảnh đất hình bình hành, biết cạnh đáy bằng \[23{\rm{ m}}\], mở rộng mảnh đất bằng việc tăng cạnh đáy mảnh đất này thêm \[{\rm{5 m}}\] thì được mảnh đất hình bình hành mới có diện tích lớn hơn mảnh đất ban đầu là \[115{\rm{ }}{{\rm{m}}^2}\]. Tính diện tích mảnh đất hình bình hành ban đầu.
Lời giải
Dựa vào công thức tính diện tích hình bình hành:
- Theo đầu bài, diện tích mảnh đất hình hành mới bằng \[115{\rm{ }}{{\rm{m}}^2}\].
- Do đó, chiều cao của mảnh đất là \[115{\rm{ : 5 = 23 m}}\].
- Vì thế diện tích mảnh đất hình bình hành ban đầu là \[23.{\rm{ }}23 = 529{\rm{ }}{{\rm{m}}^2}\].
Bài 4:
Một mảnh đất hình bình hành có cạnh đáy là \[27{\rm{ m}}\]. Người ta thu hẹp lại mảnh đất do bằng việc cắt giảm đáy của hình bình hành này khoảng nên hình bình hành mới có diện tích nhỏ hơn mảnh đất ban đầu là \[15{\rm{ }}{{\rm{m}}^2}\]. Tính diện tích mảnh đất hình bình hành ban đầu.
Lời giải
Theo đầu bài, diện tích mảnh đất hình thoi bị cắt đi là \[15{\rm{ }}{{\rm{m}}^2}\].
Do đó, chiều cao của mảnh đất là \[15{\rm{ : 5 = 3 }}{{\rm{m}}^2}\].
Vì thế, diện tích của mảnh đất hình bình hành ban đầu là \[3.{\rm{ 27 = 81 }}{{\rm{m}}^2}\].
Bài 5:
Mảnh đất hình bình hành có cạnh đáy là \(47\,m\), mở rộng mảnh đất bằng cách tăng các cạnh đáy của hình bình hành này thêm \(7\,m\) thì được mảnh đất hình bình hành mới có diện tích hơn diện tích mảnh đất ban đầu là \(189\,{m^2}\). hãy tính diện tích mảnh đất ban đầu.
Lời giải
Phần diện tích tăng thêm chính là diện tích hình bình hành có cạnh đáy \(7\,m\) và chiều cao là chiều cao của mảnh đất hình bình hành ban đầu.
Chiều cao mảnh đất là: \[189{\rm{ }}:{\rm{ }}7{\rm{ }} = {\rm{ }}27{\rm{ }}\left( m \right)\]
Diện tích mảnh đất hình bình hành ban đầu là: \[27{\rm{ x }}47{\rm{ }} = {\rm{ }}1269{\rm{ }}\left( {{m^2}} \right)\]
Bài 6:
Cho hình bình hành có chu vi là \(480\,cm\), có độ dài cạnh đáy gấp 5 lần cạnh kia và gấp 8 lần chiều cao. Tính diện tích hình bình hành
Lời giải
Ta có nửa chu vi hình bình hành là: \[480{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}240{\rm{ }}\left( {cm} \right)\]
Nếu như coi cạnh kia là 1 phần thì cạnh đáy chính là 5 phần như vậy.
Ta có cạnh đáy hình bình hành là: \[240{\rm{ }}:{\rm{ }}\left( {5 + 1} \right){\rm{ x }}5{\rm{ }} = {\rm{ }}200{\rm{ }}\left( {cm} \right)\]
Tính được chiều cao của hình bình hành là: \[200{\rm{ }}:{\rm{ }}8{\rm{ }} = {\rm{ }}25{\rm{ }}\left( {cm} \right)\]
Diện tích của hình bình hành là: \[200{\rm{ x }}25{\rm{ }} = {\rm{ }}5000{\rm{ }}\left( {c{m^2}} \right)\]
Bài 7:
Cho hình bình hành có chu vi là \(364\,cm\) và độ dài cạnh đáy gấp 6 lần cạnh kia; gấp 2 lần chiều cao. Hãy tính diện tích hình bình hành đó
Lời giải
Nửa chu vi hình bình hành là: \[364{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}182{\rm{ }}\left( {cm} \right)\]
Cạnh đáy gấp 6 lần cạnh kia nên nửa chu vi sẽ gấp 7 lần cạnh kia.
Cạnh đáy hình bình hành là: \[182{\rm{ }}:{\rm{ }}7{\rm{ x }}6{\rm{ }} = {\rm{ }}156{\rm{ }}\left( {cm} \right)\]
Chiều cao hình bình hành là: \[156{\rm{ }}:{\rm{ }}2{\rm{ }} = {\rm{ }}78{\rm{ }}\left( {cm} \right)\]
Diện tích hình bình hành là: \[156{\rm{ x }}78 = 12168{\rm{ }}\left( {c{m^2}} \right)\]
Bài 8:
Một hình bình hành có cạnh đáy là \(71\,cm\). Người ta thu hẹp hình bình hành đó bằng cách giảm các cạnh đáy của hình bình hành đi được hình bình hành mới có diện tích nhỏ hơn diện tích hình bình hành ban đầu là \(665\,c{m^2}\). Tính diện tích hình bình hành ban đầu.
Lời giải
Phần diện tích giảm đi chính là diện tích hình bình hành có cạnh đáy là \(19\,cm\) và chiều cao là chiều cao mảnh đất hình bình hành ban đầu.
Chiều cao hình bình hành là: \[665{\rm{ }}:{\rm{ }}19{\rm{ }} = {\rm{ }}35{\rm{ }}\left( {cm} \right)\]
Diện tích hình bình hành đó là: \[71{\rm{ x }}35{\rm{ }} = {\rm{ }}2485{\rm{ }}\left( {c{m^2}} \right)\]